Scientific journal

Fundamental research

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

Решения прямой и обратной спектральных задач колебаний модели вагона связаны с тем, что в ряде случаев колебания мешают нормальной эксплуатации вагона или даже непосредственно угрожают прочности, постепенно подготавливая усталостное разрушение; в таких случаях теория может указать пути для уменьшения вредных колебаний.

В настоящее время широкое развитие имеет направление, возникшее на стыке теории механизмов с акустикой, решающее задачи безразборной диагностики технических конструкций [2, 3, 5–7].

Свободные колебания механических систем, в том числе вагонов, их моделей, находят описание во многих работах по теории колебаний (см., например, [1, 8, 9]). Но в них рассматриваются прямые задачи по определению частот колебаний модели вагона. В представленной работе по прямой задаче исследована зависимость частот колебаний модели вагона от ее жесткостных и массовых параметров. Впервые поставлены и решены обратные задачи диагностирования параметров модели вагона по известным частотам ее свободных колебаний.

Прямая задача определения частот колебаний модели вагона

Рассмотрим собственные колебания модели вагона [9], представленной на рисунке.

Рассматривается консервативная система, которой дано начальное возмущение, переводящее систему в колебательный процесс. Сила инерции массы m1:

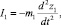
где 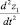 – ускорение массы m1 при ее перемещении z1. Внешняя сила, действующая на массу m1, определяется сжатием рессоры, равна c1(z1 – z2) и направлена навстречу силе I1 (рисунок, б):

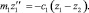
Внешними силами по отношению к массе m1 являются сила, передаваемая нижним концом верхней пружины c1(z1 – z2), и сила, вызванная деформацией нижней пружины, – c2z2. Значит, для сил, действующих на массу m2, справедливо уравнение

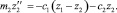
В итоге получим следующую систему дифференциальных уравнений, определяющую свободные колебания модели вагона:

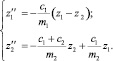(1)

Полагая, что механическая система совершает свободные гармонические колебания, решение системы (1) рассматриваем в виде

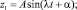
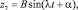
где A и B – амплитуды; λ – неизвестная угловая частота собственных колебаний.

Подставив решения z1 и z2 в систему (1), получим систему уравнений, решая которую относительно ненулевых амплитуд колебаний A и B, имеем:

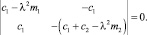
Раскрыв определитель, получим частотное уравнение свободных колебаний модели вагона:

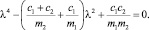(2)

Решая уравнение (2), получим аналитические формулы для частот колебаний модели:

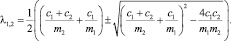(3)

Таким образом, по формуле (3) при известных массах вагона и колеса и жесткостях рессоры и рельсового основания можно определять частоты колебаний системы. Решение прямой задачи рассмотрим на конкретном примере.

Пример 1. Определить частоты колебаний модели вагона, для которого известны параметры

m1 = 23000 кг;

m2 = 4000 кг;

c1 = 7800 Н/м;

c2 = 2890 Н/м. (4)

Решение

Частотное уравнение (2) после подстановки в него заданных параметров (4) принимает вид

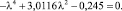
Решение, найденное с помощью ЭВМ:

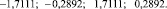
Следовательно, частоты колебаний модели вагона: λ1 = 0,2892 с–1, λ2 = 1,7111 с–1. Эти же частоты колебаний получим, подставляя заданные физические параметры в формулы (3).

Исследуем влияние жесткостных параметров модели вагона на частоты ее колебаний. Рассмотрим физические параметры (4) и будем менять, например, жесткость рессоры при неизменных остальных параметрах модели. Результаты решений прямой задачи (табл. 1) показывают что увеличение коэффициента жесткости рессоры ведет к увеличению частот колебаний модели вагона.

Таблица 1

Зависимость частот λi от жесткости c1 рессоры при параметрах (4) модели вагона

Подобные зависимости устанавливаются и при увеличении коэффициента жесткости рельсового основания или одновременном увеличении жесткостных параметров модели, что подтверждают, например, табл. 2 и 3.

Таблица 2

Зависимость частот λi от жесткости c2 рельсового основания при параметрах (4) модели вагона

Таблица 3

Зависимость частот λi от коэффициентов жесткостей c1, c2 при параметрах (4) модели вагона

Аналогичные исследования проведены по влиянию массовых параметров модели вагона на частоты ее колебаний, и получено, что увеличение масс ведет, наоборот, к уменьшению частот колебаний. Например, в табл. 4 и 5 приведены зависимости частот колебаний от массы вагона и массы колеса вагона.

Таблица 4

Зависимость частот λi от массы m1 вагона при параметрах (4) модели вагона

Таблица 5

Зависимость частот λi от массы m2 колеса при параметрах (4) модели вагона

Проведенные исследования по влиянию физических параметров модели вагона на частоты ее свободных колебаний важны при решении проблемы сохранения безопасных частот колебаний механической системы при изменениях ее параметров. Последнюю проблему можно будет решить с помощью метода решения обратной спектральной задачи.

Обратная задача диагностирования параметров модели вагона

Поставим к прямой спектральной задаче обратную – задачу диагностирования жесткостных и массовых параметров модели вагона по известным частотам ее колебаний. Рассмотрим вначале задачу диагностирования жесткостных параметров модели.

Обратная задача. Известны частоты колебаний модели вагона и массовые параметры. Неизвестны жесткостные параметры: коэффициенты рессоры и рельсового основания.

Исследуем вопрос о единственности решения поставленной обратной задачи [6]. При решении прямой задачи было получено уравнение (3), которое преобразуем к виду

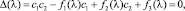(5)

где функции fi(λ) (i = 1, 2, 3) выражаются через частоту колебаний и массовые параметры:

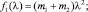
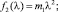
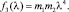
Введем обозначения: задачу с частотным уравнением (5) и жесткостями c1 и c2 рессоры и рельсового основания обозначим через L, а задачу с такими же массовыми параметрами модели, но с другими жесткостями и 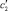 рессоры и рельсового основания обозначим через L′. Частотное уравнение задачи L′ будет иметь вид

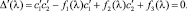(6)

Справедлива теорема.

Теорема 1. Если собственные частоты задач L и L′ с характеристическими определителями Δ(λ) и Δ′(λ) совпадают с учетом их кратностей, то 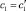и .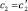

Доказательство. Собственные частоты задачи L являются корнями целой функции [4] – частотного уравнения (5), а собственные частоты задачи L′ – корнями уравнения (6). Причем функции fi(λ) (i = 1, 2, 3) не зависят от коэффициентов жесткостей c1 и c2 и образуют систему линейно независимых функций.

Так как функции Δ(λ) и Δ′(λ) являются целыми функциями от λ и не равны тождественно нулю, то они восстанавливаются по своим нулям с точностью до постоянного множителя K. Значит, 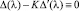. Из линейной независимости функций fi(λ) (i = 1, 2, 3) и последнего равенства имеем K = 1. Значит, 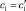и 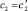. Теорема доказана.

Из теоремы следует, что жесткостные параметры можно восстановить по известным значениям собственных частот колебаний модели вагона.

Построим теперь метод определения жесткостных параметров модели. Пусть известны две собственные частоты λ1 и λ2, тогда имеем систему уравнений

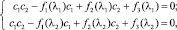(7)

из которой с учетом функций fi(λ) (i = 1, 2, 3) получим аналитические выражения для коэффициентов жесткостей рессоры и рельсового основания:

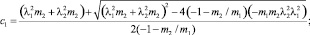
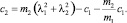(8)

Таким образом, если известны две собственные частоты колебаний модели вагона, то жесткостные параметры определяются по формулам (8).

Пример 2. Определить жесткость рессоры и рельсового основания, если для модели вагона известны частоты колебаний

λ1 = 0,2892 с–1,

λ2 = 1,7111 с–1

и массовые параметры

m1 = 23000 кг;

m2 = 4000 кг.

Решение

Подставляя заданные частоты колебаний и массовые параметры в формулы (8), имеем

c1 = 7799,9999;

c2 = 2889,9999.

Значит, жесткости равны

c1 = 7800 c–1;

c2 = 2890 c–1.

Заметим, что значения c1, c2 определены верно, так как по решению прямой задачи именно этим жесткостям рессоры и рельсового основания соответствуют заданные значения частот модели вагона.

Поставим теперь обратную задачу диагностирования массовых параметров модели вагона.

Обратная задача. Известны частоты колебаний модели вагона и жесткостные параметры. Неизвестны массовые параметры: масса вагона и масса колеса.

Частотное уравнение (2) преобразуем к виду

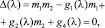(9)

в котором функции gi(λ) (i = 1, 2, 3) имеют вид

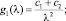
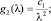
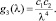
Так же, как и при решении обратной задачи диагностирования жесткостных параметров, исследована единственность решения поставленной задачи. При этом рассмотрены: V – задача с массами m1, m2 и частотным уравнением (9), V′ – задача с массами 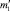, 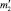и частотным уравнением

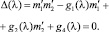
Доказана теорема.

Теорема 2. Если собственные частоты задач V и V′ с характеристическими определителями Δ(λ) и Δ′(λ) совпадают с учетом их кратностей, то

;

.

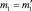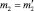Приведем метод определения массовых параметров. Если известны значения двух частот колебаний модели вагона, то имеем систему уравнений вида (9), из которой получим аналитическое решение относительно массы вагона и массы колеса:

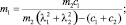
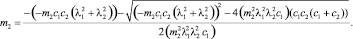(10)

Пример 3. Известны частоты колебаний λ1 = 0,2892 с–1, λ2 = 1,7111 с–1 модели вагона и жесткостные параметры c1 = 7800 Н/м; c2 = 2890 Н/м. Необходимо найти массу вагона и массу колеса.

Решение

Подставляя заданные частоты и жесткостные параметры в формулы (10), находим, что m1 = 23000 кг; m2 = 4000 кг. Заметим снова, что значения масс m1, m2 определены верно, что подтверждает решение прямой спектральной задачи при заданных параметрах модели вагона.

Заключение

Исследована прямая задача определения частот свободных колебаний пружинно-массовой модели вагона. Впервые поставлены обратные задачи – задачи диагностирования физических параметров модели вагона по известным частотам ее свободных колебаний. Решены обратные задачи определения жесткостных и массовых характеристик модели вагона. Исследована единственность решения задач, доказаны соответствующие теоремы. Получены аналитические формулы для определения коэффициентов жесткостей рессоры и рельсового основания, а также для масс вагона и колеса. Предложены методы решения задач, использующие значения двух частот колебаний модели вагона. Приведены примеры решений обратных задач.

Методы решений обратных задач можно использовать при решении проблемы сохранения безопасных частот колебаний модели вагона при изменениях ее жесткостных и массовых параметров.

Урманчеев С.Ф., д.ф.-м.н., профессор, директор, ФГБУН «Институт механики им. Р.Р. Мавлютова» Уфимского научного центра РАН, г. Уфа;

Ахтямов А.М., д.ф.-м.н., проф., зав. кафедрой механики сплошных сред, ФГБОУ ВПО «Башкирский государственный университет», г. Уфа.

Работа поступила в редакцию 01.04.2015.