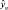В современном мире отходы – это основной фактор антропогенного воздействия на окружающую среду, последствия которого в значительной степени, определяют ухудшение условий жизни человека. Отходы являются источником более 60 % неблагоприятных воздействий на человека и природу. Поэтому в связи с ухудшением экологической обстановки во всем мире проблема обезвреживания, переработки и утилизации отходов с каждым годом становится все более важной и актуальной.
Самым эффективным способом утилизации отходов полимерных материалов является их вторичная переработка [7, 8]. Возможность использования полимерных отходов для повторного производства ограничивается их нестабильными и худшими по сравнению с исходными полимерами механическими свойствами, поэтому необходимо модифицировать полимерные отходы. Одним из способов модификации полимеров является использование наполнителей, т.е. создание полимерных композиций [2, 4]. В качестве наполнителей можно использовать техногенное минеральное сырьё, источником которого являются отходы горнодобывающих и металлургических предприятий [3]. Для улучшения свойств получаемого композита применяют вспениватели, при выборе которых необходимо учитывать особенности переработки полимера [6].
Цель исследования: определение оптимальных условий получения композиционного материала на основе отходов упаковки из полипропилена и техногенного минерального сырья (доменный шлак ОАО «ММК») методом полного факторного эксперимента.
Материалы и методы эксперимента
Образцы отходов полимерной упаковки из полипропилена предварительно нарезаются и дробятся на лабораторной дробилке до однородной фракции. Для проведения испытаний выбрана лабораторная установка, состоящая из нагревательной печи и специально изготовленной лабораторной пресс-формы, имеющей камеру.
Изменение температуры в камере печи производится с помощью регулирования подаваемого напряжения на нагревательную спираль, измерение температуры производится ртутным термометром. После проведения серии предварительных наладочных испытаний, температура в камере была установлена на уровне 230 °С, что позволило за 20 минут равномерно расплавлять полимер, не приводя к деструкции его по краям формы.
С целью уменьшения плотности получаемого материала использовался промышленный вспениватель для ПП азодикарбонамид марки ЧХЗ-21 (производитель – Китай). В результате каждого испытания получался образец материала цилиндрической формы строго определенного диаметра (27 мм – диаметр формы), различной высоты (связано со вспениванием) и массы (связано с потерями материала через неплотно установленное дно формы).
Взвешивание навесок для образцов, а также полученных образцов продукта производилось на электронных весах с точностью до 0,001 г. Измерение линейных размеров (для определения плотности) проводилось штангенциркулем.
Результаты исследования и их обсуждение
Методом построения математической модели получения композитов выбран регрессионный анализ результатов проведения многофакторного эксперимента [1, 5].
В качестве выходного параметра, имеющего значение для потребителя, выбрана плотность готового продукта, так как вес единицы продукции является одним из главных параметров при определении не только и не столько сфер применения готового продукта, но в первую очередь, экономических параметров технологии, что, в условиях вторичной переработки отходов производства является одним из определяющих факторов.
Следующие факторы, варьирование которых в условиях лаборатории можно осуществить достаточно точно, исключив погрешности, были управляющими: время проведения испытания t, концентрация вспенивателя C, давление на поршень P.
При условии сохранения постоянства навески исследуемого материала в каждом опыте и температуры в рабочей камере нагревательной печи был проведен полный многофакторный эксперимент, состоящий из серии опытов, в каждом из которых было установлено уникальное сочетание значений управляющих факторов. Результаты проведения эксперимента были проанализированы для установления зависимости выходного значения от каждого фактора или их сочетаний.
В результате данного эксперимента была определена зависимость плотности композиционного материала ρ (Y) от времени переработки t (X1), концентрации вспенивателя С (Х2) и давления на поршень Р (Х3). Уровни варьирования факторов представлены в табл. 1. При этом в рамках проведения испытаний обеспечивалось постоянство температуры в печи (230 °С).
При реализации полного многофакторного эксперимента руководствовались картой проведения эксперимента, содержащей матрицу планирования (закодированные значения изменяемых факторов для каждого опыта) и порядок реализации опыта в каждой серии испытаний (всего проведено 3 серии), составленный произвольно (рандомно).
Полученные значения выхода (плотности материала) занесены в табл. 2, также в нее занесены средние значения плотности, полученные в трех сериях для каждого опыта, рассчитанные по формуле.
Построчные средние значения плотности рассчитаны по формуле (1)
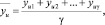 (1)
(1)
где γ – число повторных опытов.
Таблица 1
Уровни варьирования факторов
|
Уровни |
Кодировка в матрице планирования |
Факторы |
||
|
Время t, мин |
Концентрация вспенивателя С, % |
Давление Р, кг/см3 |
||
|
Основной |
– |
20 |
4,0 |
50 |
|
Нижний |
–1 |
17 |
2,0 |
35 |
|
Верхний |
+ 1 |
23 |
6,0 |
65 |
|
Интервал варьирования |
3 |
2,0 |
15 |
|
Таблица 2
Карта проведения эксперимента
|
Номер опыта |
Порядок реализации опыта (рандомный) |
Матрица планирования |
Полученное значение плотности |
Среднее |
Расчётное значение |
||||||
|
Х1 |
Х2 |
Х3 |
Y1 |
Y2 |
Y3 |
||||||
|
1 |
2 |
7 |
3 |
–1 |
–1 |
–1 |
0,389 |
0,370 |
0,390 |
0,383 |
0,3832 |
|
2 |
7 |
4 |
8 |
–1 |
–1 |
+1 |
0,431 |
0,387 |
0,415 |
0,411 |
0,4108 |
|
3 |
4 |
5 |
2 |
–1 |
+1 |
–1 |
0,420 |
0,413 |
0,436 |
0,423 |
0,4232 |
|
4 |
8 |
2 |
7 |
–1 |
+1 |
+1 |
0,681 |
0,685 |
0,671 |
0,679 |
0,6788 |
|
5 |
6 |
8 |
6 |
+1 |
–1 |
–1 |
0,624 |
0,652 |
0,617 |
0,631 |
0,6308 |
|
6 |
3 |
1 |
5 |
+1 |
–1 |
+1 |
0,549 |
0,513 |
0,525 |
0,529 |
0,5289 |
|
7 |
5 |
6 |
1 |
+1 |
+1 |
–1 |
0,790 |
0,810 |
0,785 |
0,795 |
0,7948 |
|
8 |
1 |
3 |
4 |
+1 |
+1 |
+1 |
0,890 |
0,870 |
0,859 |
0,873 |
0,8732 |
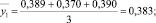
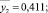
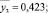
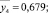
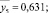
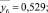
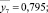
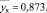
Результаты расчета занесены в столбец 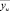 карты проведения эксперимента (табл. 2).
карты проведения эксперимента (табл. 2).
Построчные дисперсии, (г/см3)2, (дисперсии воспроизводимости) определены по формуле (2)
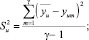 (2)
(2)
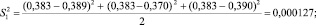
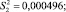
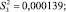
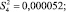
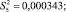
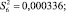
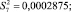
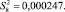
Сумма построчных дисперсий рассчитана по формуле (3)
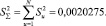 (3)
(3)
Воспроизводимость опытов проверена по критерию Кохнера по формуле (4):
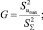 (4)
(4)
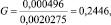
где 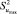 – максимальная из построчных дисперсий.
– максимальная из построчных дисперсий.
Если G < GT, то опыты равноточны (GT – табличные значения критерия Кохрена, выбираемые в зависимости от N, γ и уровня значимости (надежности)).
Для данного случая при N = 8, γ = 3, p = 0,95, GT = 0,438. Тогда 0,2446 < 0,438 (G < GT), следовательно, опыты равноточны.
Коэффициенты уравнения регрессии, определённые по формулам (5), (6), составили
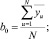 (5)
(5)
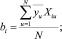 (6)
(6)
b0 = 0,5905; b1 = 0,1165; b2 = 0,102;
b3 = 0,0325; b12 = 0,025; b23 = 0,051;
b13 = –0,0385; b123 = –0,006.
Дисперсия эксперимента определена по формуле (7)
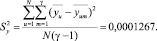 (7)
(7)
Усредненная дисперсия эксперимента с учетом повторных опытов по формуле (8)
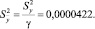 (8)
(8)
Ошибка и средняя квадратичная ошибка коэффициентов регрессии рассчитаны по формулам (9), (10):
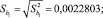 (9)
(9)
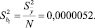 (10)
(10)
При числе степеней свободы f2 = 16 (формула f2 = N(γ – 1)) и уровня значимости р = 0,05 табличное значение критерия Стьюдента t = 2,119. Тогда значение доверительного интервала определяется по формуле (11)
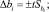 (11)
(11)
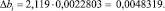
Сравнивая величины полученных коэффициентов с доверительным интервалом, выбираем только те, абсолютная величина которых больше этого интервала:
b0 = 0,5905; b1 = 0,1165; b2 = 0,102;
b3 = 0,0325; b12 = 0,025; b23 = 0,051;
b13 = –0,0385; b123 = –0,006.
Таким образом, значимыми оказались 8 коэффициентов, поэтому уравнение регрессии имеет следующий вид:
Y = 0,5905 + 0,1165Х1 + 0,102Х2 + 0,0325Х3 + 0,025Х1Х2 + 0,051Х2Х3 – 0,0385Х1Х3 – 0,006Х1Х2 Х3
или
ρ = 0,5905 + 0,1165t + 0,102C + 0,0325P + 0,025TC + 0,051CP – 0,0385tP – 0,006tCP.
Далее проверили адекватность (пригодность) модели, т.е. насколько хорошо полученное уравнение описывает результаты эксперимента в исследуемой области.
Для этого использовали критерий Фишера (формула (12)):
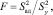 (12)
(12)
где 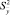 – усредненная дисперсия эксперимента;
– усредненная дисперсия эксперимента; 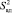 – дисперсия адекватности или остаточная дисперсия (формула (13)):
– дисперсия адекватности или остаточная дисперсия (формула (13)):
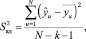 (13)
(13)
где 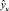 – рассчитанные по полученному уравнению значения выхода при значениях кодированных переменных, соответствующих каждой из строк матрицы планирования;
– рассчитанные по полученному уравнению значения выхода при значениях кодированных переменных, соответствующих каждой из строк матрицы планирования; 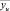 – усредненное значение выхода, полученное при реализации повторных опытов для соответствующей строки.
– усредненное значение выхода, полученное при реализации повторных опытов для соответствующей строки.
Модель можно считать адекватной, если F < Fтабл. Табличное значение критерия Фишера находят в зависимости от числа степеней свободы
f1 = N – k – 1 и f2 = N(γ – 1),
где N – число вариантов опытов (строк) в матрице планирования; K – число варьируемых факторов; γ – число повторных опытов.
Для определения 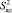 вычислили сначала значения выхода, предсказываемые полученным выше уравнением регрессии (табл. 1), затем получили значение
вычислили сначала значения выхода, предсказываемые полученным выше уравнением регрессии (табл. 1), затем получили значение 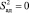 , 00000008.
, 00000008.
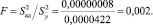
Табличное значение критерия Фишера Fтабл = 3,01 при уровне значимости 0,05 и f1 = 4 и f2 = 16.
F < Fтабл, т.е. имеются основания сделать вывод о том, что полученная модель адекватна.
Заключение
В результате реализации полного многофакторного эксперимента и регрессионного анализа полученных данных составлена математическая модель, отражающая зависимость таких технологических параметров, как время обработки, концентрация вспенивателя марки ЧХЗ-21 и давления на плотность готового продукта в результате получения его в пресс-форме. Модель отражает зависимость плотности полимера от всех выбранных факторов (с учетом коэффициентов) в отдельности, от сочетания двух факторов (совместного влияния): температуры и концентрации, концентрации и давления, температуры и давления, а также от сочетания всех трех факторов. Наибольшее влияние от двух факторов имеет сочетание давления и концентрации. Это влияние можно объяснить механизмом вспенивания: поскольку разложение вспенивателя в объеме пробы происходит постепенно и зависит от температуры, которая в момент прогрева формы различна в объеме, единственным сдерживающим фактором, не позволяющим пузырькам газа сформироваться и затем покинуть объем до отверждения материала, является внешнее избыточное давление. При сохранении избыточного давления происходит сдерживание процесса вспенивания образца, при снятии давления образец может свободно расширяться. Поэтому для достижения максимальной эффективности процесса вспенивания необходимо увеличение давления в момент оплавления полимера и резкое снятие его по окончании процесса.
Рецензенты:Бигеев В.А., д.т.н., профессор, директор института металлургии, машиностроения и металлообработки, ФГБОУ ВПО «Магнитогорский государственный технический университет им. Г.И. Носова», г. Магнитогорск;
Стеблянко В.Л., д.т.н., профессор, ФГБОУ ВПО «Магнитогорский государственный технический университет им. Г.И. Носова», г. Магнитогорск.
Работа поступила в редакцию 01.04.2015.




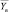 , г/см3
, г/см3