В практике моделирования исследователям часто приходится сталкиваться с ситуацией, когда объект анализа (система) естественным образом «распадается» на составляющие (подсистемы), поведение которых также представляет интерес.
При этом, следуя канонам системного анализа, как правило, исходная система формализуется методами математического моделирования «лучше», адекватнее, чем её составные части. Более того, один из принципов системного анализа гласит: «Не элементы составляют систему, а система распадается на элементы». Это означает, что чем крупнее объект исследования, тем более точную модель можно построить, чем инерционнее будет этот объект, тем устойчивее будут закономерности его функционирования.
Небольшой, несколько утрированный, но показательный пример: поведение водоема «смоделировать» гораздо проще, чем поведение отдельной молекулы.
Итак, пусть необходимо построить иерархическую (для определенности, двухуровневую) одномерную статистическую модель, описывающую переменную z регрессией
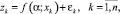(1)
где k – номер наблюдения обрабатываемой выборки длины n; f – вещественная аппроксимирующая функция; α – вектор оцениваемых параметров; xk – вектор экзогенных переменных модели; εk – ошибки аппроксимации. Пусть исследуемый объект (допустим, каскад электростанций; z – объем произведенной на нем электроэнергии) состоит из r составных частей (отдельных электростанций), для каждой из которых построена своя модель:
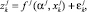
(2)
Обозначения здесь очевидны.
При оценивании параметров регрессионного уравнения (2) и оценки его качества можно использовать, в частности, следующие работы [1–5, 7, 8, 10].
На предыстории процесса выполняется естественное равенство
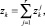
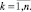(3)
Как правило, одно из основных направлений использования моделей (1), (2) – прогнозирование с их помощью будущего состояния объектов.
Обозначим через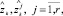 
k > n прогнозные значения соответствующих переменных. При этом в общем случае равенство (3) может нарушаться, т.е.
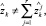k > n.
Возникает вопрос: что делать с образующимся дисбалансом
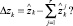
Для его решения воспользуемся идеей, высказанной в [5], а именно: дисбаланс Δzk должен быть распределен между r объектами обратно пропорционально точности соответствующих моделей. То есть чем более адекватна j-я модель (2), тем меньшая часть Δzk должна быть направлена на корректировку значения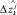 
.
К настоящему времени в регрессионном анализе разработан широкий спектр критериев адекватности статистических моделей (достаточно представительный их перечень приведен в [8]). Это, в частности, коэффициент множественной детерминации, критерии Фишера, Стьюдента и Дарбина – Уотсона, средние относительные ошибки аппроксимации и прогноза, критерии смещения и согласованности поведения и другие. Приведем эти критерии более подробно, используя, в частности, работы [11–14]. При этом во избежание путаницы зависимую переменную будем обозначать через y.
а) критерий множественной детерминации R2, выражающий степень согласованности вычисленных и фактических значений зависимой переменной, поскольку он представляет собой квадрат коэффициента корреляции между соответствующими векторами. Эквивалентная, по существу, трактовка R2 такова: он показывает, какая доля дисперсии у объясняется регрессией (1).
Формула расчета R2 имеет вид ( в случае присутствия в (1) свободного члена):
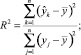
или, что то же
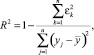
где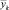 
, 
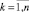– вычисленные значения зависимой переменной, 
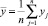– среднее значение у. Легко видеть, что всегда R2 ∈ [0, 1].
Другая, формально более аргументированная интерпретация критерия множественной детерминации состоит в том [8], что он показывает, насколько регрессия (1) лучше модели среднего. Поэтому при описании динамических процессов с помощью регрессии, содержащей трендовую составляющую
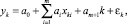
для того, чтобы сравнить, насколько такая регрессия лучше модели простого тренда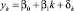 
, в [8] предлагается использовать в качестве аналога R2 показатель 
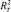, рассчитываемый по формуле
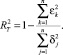
Существенным недостатком R2 является то, что он не уменьшает своих значений при добавлении в (1) новых переменных. Поэтому всегда можно сделать R2 как угодно близким к единице путем добавления в регрессию дополнительных независимых переменных. Для элиминирования этого недостатка часто вместо R2 используют его скорректированное на число степеней свободы значение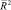 
:
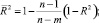
б) величина остаточной дисперсии s2, определяющая меру вариации выходного показателя относительно регрессии:
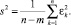
Для придания остаточной дисперсии относительного характера иногда пользуются следующей формулой:
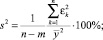
в) F-критерий Фишера, показывающий отношение дисперсии фактических значений у к остаточной дисперсии. В зависимости от существующих вариантов интерпретации этого критерия он указывает на: отсутствие (или наличие) линейной связи зависимой переменной с одной из независимых; значимость критерия R2; степень линейности уравнения. F-критерий рассчитывают по формуле
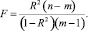
F-критерий имеет статистический характер и требует использования соответствующих таблиц F-распределения. При превышении значения F над табличным первое считается удовлетворительным. В любом случае значение F-критерия тем лучше, чем оно выше;
г) критерий Дарбина –Уотсона d, указывающий на наличие или отсутствие корреляции (положительной или отрицательной) остатков ε:
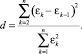
Критерий d принимает значения на отрезке [0, 4] и также требует привлечения соответствующих статистических таблиц. Идеальное его значение, указывающее на отсутствие автокорреляции остатков, равно двум.
д) t-критерий, показывающий, во сколько раз оцененное значение каждого параметра регрессии (1) превышает его стандартную ошибку. Этот критерий служит мерой вариации каждого параметра и так же, как критерия f и d, требует привлечения соответствующих таблиц распределения, в данном случае Стьюдента. Формула для его расчета имеет вид
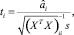
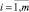
где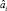 
– оцененное значение i-го параметра регрессии (1), 
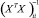– i-й диагональный элемент матрицы 
.
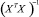Удовлетворительным считается значение t-критерия, превышающее единицу. В противном случае соответствующий регрессор считается незначимым;
е) cредняя относительная ошибка аппроксимации E. Это обычно применяемый в инженерных расчетах показатель, вычисляемый по формуле
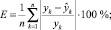
ж) cредняя относительная ошибка прогноза 
, рассчитанная по экзаменующей выборке следующим образом.
Вся выборка делится на две части – большую (обучающую) с номерами наблюдений 1, 2, …, τ и меньшую (экзаменующую) с номерами τ+1, τ+2,…,n. По наблюдениям обучающей выборки определяются параметры регрессии (1) â, после чего значение 
вычисляется по формуле
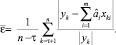
Данный критерий служит оценкой прогностических возможностей построенного уравнения. Естественно, после их проверки параметры регрессии пересчитываются по полной выборке;
з) критерий смещения nсм, представляющий собой меру «стабильности» оценок параметров относительно различных участков выборки.
Для расчета этого критерия вся выборка делится примерно пополам, и для каждой части определяются оценки параметров 
и 
.
Тогда значение nсм принимает вид
Из этой формулы следует, что значение критерия nсм чем меньше, тем лучше.
Необходимо отметить, что обычно в литературе использование приведенных критериев носит традиционно пассивный характер, выражающийся в неформальном доказательстве удовлетворительности качества построенной модели в случае попадания значений критериев в требуемые интервалы.
Пусть в качестве основного нами выбран критерий «средняя относительная ошибка аппроксимации». Рассчитаем его значение для каждой из r моделей (2):
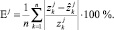
Вычислим корректирующие элементы по очевидной формуле:
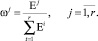
После этого прогнозные значения 
уточняются следующим образом:
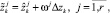k > n.
В своих последующих работах авторы намерены продолжить развивать предлагаемый здесь подход.
Рецензенты:Кузьмин О.В., д.ф.-м.н., профессор, заведующий кафедрой теории вероятностей и дискретной математики, Иркутский государственный университет, г. Иркутск;
Лакеев А.В., д.ф.-м.н., ведущий научный сотрудник, Институт динамики систем и теории управления СО РАН, г. Иркутск.
Работа поступила в редакцию 18.03.2015.