В настоящее время в лесной отрасли важное значение имеет распределение перевозок между железнодорожным и автомобильным транспортом. Целесообразным признается тот способ перевозки, при котором достигается меньшая сумма приведенных затрат [4].
Рассмотрим экономико-математическую модель вида
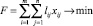(1)
при
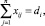i = 1, 2, ..., m; (2)
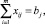j = 1, 2, ..., n; (3)
xij ≥ 0, i = 1, 2, ..., m, j = 1, 2, ..., n.
где m – количество станций погрузки; n – количество станций выгрузки; di – объемы погрузки; bj – объемы выгрузки; lij – кратчайшие (тарифные) расстояния между станциями погрузки и выгрузки; xij – искомые объемы перевозок.
Для определения рациональных зон снабжения лесоматериалами и заполнения «свободных участков» рассчитываются потенциалы транзитных станций по формуле
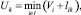(4)
где I – множество станций погрузки; Vi – потенциал i-й станции погрузки; lik – кратчайшее (тарифное) расстояние между i-й станцией погрузки и k-й транзитной станцией; Uk – искомый потенциал k-й транзитной станции.
Для каждой i-й станции погрузки оптимальная схема лесных грузопотоков разрешает перевозку в адрес только таких станций j, для которых выполняется условие
Vj = Vi + lij. (5)
Для выбора плана с наименьшими расходами решается задача:
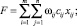(6)
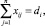i = 1, 2, ..., m; (7)
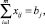j = 1, 2, ..., n; (8)
(9)
где сij – зависящие от параметров движения эксплуатационные расходы железнодорожного транспорта на перевозку единицы лесопродукции от i-й станции погрузки до j-й станции выгрузки.
При этих условиях сохраняются устойчивые транспортные связи. Задача решается путем максимизации коэффициента устойчивости связей (Kc) [5]:
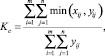(10)
при условии
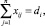i = 1, 2, ..., m; (11)
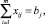j = 1, 2, ..., n; (12)
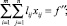(13)
xij ≥ 0, i = 1, 2, ..., m, j = 1, 2, ..., n. (14)
где yij – планируемый объем перевозки от i-й станции погрузки до j-й станции выгрузки лесоматериалов; f – минимальный тарифный грузооборот (м3/км).
Учет пропускных способностей отдельных участков сети и станций реализуется соответствующим программным преобразованием расчетной транспортной сети на ЭВМ путем ввода дополнительных вершин и дуг, отражающих размеры ограничений (в м3).
При разработке оптимальной схемы грузопотоков с учетом частичной взаимозаменяемости лесопродукции оптимальное прикрепление и потенциалы, станций погрузки и выгрузки определяются следующим выражением:
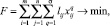(15)
при
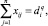q = 1, 2, ..., σ; i = 1, 2, ..., m; (16)
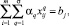j = 1, 2, ..., n; (17)
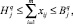
q = 1, 2, ..., σ; j = 1, 2, ..., n; (18)
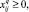i = 1, 2, ..., m;
j = 1, 2, ..., n; q = 1, 2, ..., σ, (19)
где m – число станций погрузки; n – число станций выгрузки; σ – количество видов частично взаимозаменяемой продукции; lij – кратчайшее (тарифное) расстояние перевозки от i-й станции погрузки до j-й станции выгрузки; αq – коэффициент взаимозаменяемости q-го вида продукции;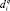 
– объем погрузки продукции q-го вида на i-й станции погрузки; bj – объем выгрузки на j-й станции выгрузки; 
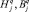– ограничения на размер потребления (выгрузки) лесоматериалов q-го вида по j-й станции выгрузки (не меньше, не больше); 
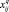– искомые объемы перевозок продукции q-го вида от i-й станции погрузки до j-й станции выгрузки.
Сформируем программным путем искусственную «многослойную» транспортную сеть. Каждому отправителю в этой сети соответствует вершина с объемом производства, равным объему погрузки. Для учета двухсторонних ограничений («не менее», «не более») на потребление отдельных видов лесоматериалов по каждому потребителю в сеть вводится 2k + 1 вершина, где k – количество видов лесоматериалов. Вершины первого слоя (k вершин) отражают нижнюю границу потребления, второго слоя (тоже k вершин) – разницу между верхней и нижней границами потребления. Балансировочная вершина необходима для учета суммарной потребности получателя продукции и является вершиной-поставщиком с объемом производства, равным разнице между суммой верхних границ потребления и реальной суммарной потребностью получателя [3].
Каждая вершина – отправитель соединяется с вершинами – потребителя первого слоя, которые соответствуют виду продукции, отгруженному отправителем. Вершины – потребители первого слоя соединяются дугами нулевой длины с «одноименными» вершинами-потребителями второго слоя. Каждая балансировочная вершина соединяется дугами нулевой длины со всеми вершинами-потребителями второго слоя, которые соответствуют тому же получателю продукции.
На сформированной указанным способом сети решается поставленная транспортная задача и определяется оптимальное прикрепление потребителей к поставщикам лесопродукции (рис. 1).
Рациональные зоны снабжения при разработке оптимальных схем грузопотоков с учетом взаимозаменяемости различных видов продукции устанавливаются следующим образом.
На рис. 2 представлена структура для разработки комплекса программ на ЭВМ.
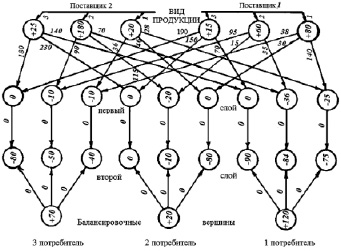
Рис. 1. Схема условной сети для решения транспортной задачи с учетом взаимозаменяемости лесной продукции
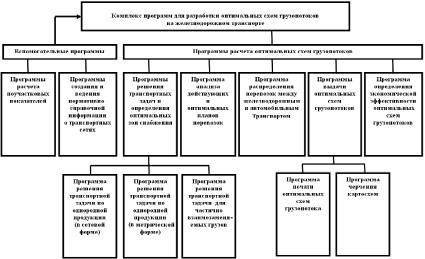
Рис. 2. Комплекс программы для разработки оптимальных схем грузопотоков лесных грузов
Для решения задачи по оптимизации грузопотоков лесоматериалов подготавливается постоянная информационная модель транспортной сети для ЭВМ. Эта транспортная сеть представляет собой закодированную информацию о включенных в неё вершинах (станциях) и оценку звеньев (участков) между ними. Размер транспортной сети определяется количеством включенных в неё вершин или участков.
Оценку звеньев (дуг) можно осуществлять по их протяженности, а также по стоимостным и временным показателям. При этом возможно определенное микрорайонирование сети, оценкой участков по направлениям «туда» и «обратно», подготовка и взаимодействие нескольких «слоёв» сети, использование ограничений по вершинам и участкам, перевод сети в матричную форму.
Разработка такой схемы грузопотоков осуществляется путем решения открытых транспортных задач (при несбалансированности ресурсов и потребностей в них) в два этапа. На первом этапе решается задача оптимального прикрепления потребителей к поставщикам при выбранном варианте развития (сокращения) производства, а на втором – выбор местоположения пунктов производства (потребления) и разработка перспективных схем грузопотоков.
Рецензенты:Сушков С.И., д.т.н., профессор кафедры технологии и машин лесозаготовок, ФГБОУ ВПО «Ухтинский государственный технический университет», г. Ухта;
Павлов А.И., д.т.н., профессор кафедры лесных, деревообрабатывающих машин и материаловедения, ФГБОУ ВПО «Ухтинский государственный технический университет», г. Ухта.
Работа поступила в редакцию 18.03.2015.