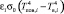Надежность трубопроводов, прокладываемых в многолетнемерзлых грунтах (ММГ), во многом зависит от динамики процесса формирования ореола растепления, обуславливающего дальнейшую просадку и недопустимый прогиб локальных участков [1–7].
Способом уменьшения величины ореола растепления вокруг «горячего» трубопровода служит устройство теплоизоляционного покрытия. Выбор параметров теплоизоляции зависит от результатов теплотехнического расчета, повышение достоверности которого является актуальной проблемой проектирования трубопроводов в условиях криолитозоны.
Цель исследования – совершенствование методики расчета ореола растепления вокруг «горячего» трубопровода, проложенного в ММГ.
Задачи:
– выполнить анализ методики составления прогноза теплового режима грунтов, регламентируемой нормативно-технической документацией (НТД) РФ [10];
– оценить величину теплового потока, переносимого посредством излучения в инфракрасной (ИК) области спектра;
– разработать методику расчета теплового режима ММГ, учитывающую теплообмен поверхности грунта с атмосферой, посредством ИК излучения;
– сопоставить результаты моделирования с данными натурных термометрических наблюдений ММГ в естественном состоянии;
– оценить изменения расчетных глубин протаивания ММГ под трубопроводом в динамике по существующей и предложенной методикам.
При инженерно-геологическом обосновании строительства и реконструкции магистральных трубопроводов для составления прогноза теплового режима грунтов применяется инженерная методика нормативного документа [10] (далее по тексту – методика I). Она содержит основные алгоритмы решения дифференциального уравнения теплопроводности методом конечных разностей при граничных условиях третьего рода.
Методика I реализована в различных программных продуктах (TermoStab Universal, Frost 3D Universal) и находит применение в инженерных расчетах благодаря своей гибкости и универсальности. Моделирование по методике I проводится в три этапа:
Этап I – ввод исходных данных. Создание геометрической модели грунта и задание граничных условий (рис. 1). Для задания граничных условий и свойств ММГ непосредственно из материалов инженерных изысканий в модель вводятся следующие данные: теплофизические характеристики грунтов (теплоемкость, теплопроводность, плотность); среднемесячная температура атмосферного воздуха; величина суммарной солнечной радиации и альбедо деятельной поверхности при средних условиях облачности; среднедекадная толщина и плотность снежного покрова.
Такие величины, как коэффициент конвективной теплоотдачи и теплопроводность снежного покрова, не входят в материалы инженерных изысканий и выбираются по справочным таблицам различных авторов [9].
Этап II – калибровка модели грунта. Конечной целью второго этапа является корректировка модели грунта таким образом, чтобы расчетная и измеренная температуры на глубине нулевых годовых амплитуд совпадали. Варьирование осуществляется изменением значений коэффициента конвективной теплоотдачи и теплопроводности снежного покрова.
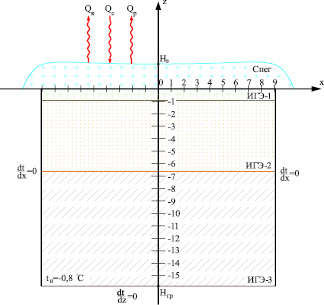
Рис. 1. Схема теплового режима ММГ и основные граничные условия: Qк – конвективный тепловой поток; Qс – поток тепла от солнечной радиации; Qр – радиационный поток тепла в ИК области спектра; Hs – высота снежного покрова; Hгр – глубина моделируемого грунтового основания, соответствующая границе нулевой годовой амплитуде температуры; tн – начальная температура грунта на глубине нулевых годовых амплитуд; ИГЭ-1, 2, 3 – инженерно-геологические элементы
Этап III – расчет ореола растепления. В откалиброванную модель грунта вводится проектируемый трубопровод с заданным диаметром, толщиной стенки, параметры теплоизоляционного покрытия и температура перекачиваемого продукта.
Для установления возможности управления расчетной температурой на глубине нулевых годовых амплитуд при помощи изменения параметров, приведенных во втором этапе, обратимся к формуле, задающей граничные условия третьего рода на поверхности калибруемой модели грунта [8]:
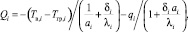 (1)
(1)
где Q – тепловой поток от грунта в атмосферу; a – коэффициент конвективной теплоотдачи, зависящий от скорости ветра и шероховатости подстилающей поверхности грунта; λ – коэффициент теплопроводности снега, зависящий от его плотности и влажности; δ – толщина снежного покрова; Tв и Tгр – соответственно температура атмосферного воздуха и температура поверхности грунта; q – поток тепла от солнечной радиации, индекс i относится к i-му месяцу в году.
Очевидно, что изменение коэффициента конвективной теплоотдачи a или теплопроводности снега λ в большую сторону в процессе калибровки повышает тепловой поток от грунта в атмосферу Q в зимний период, что приводит к искусственному переохлаждению и снижению температуры на глубине нулевых годовых амплитуд. Искусственное завышение потока тепла Q от грунта в атмосферу в зимний период может приводить к значительному снижению расчетной величины ореола оттаивания под малозаглубленными трубопроводами.
Обоснование необходимости учета теплообмена посредством ИК излучения
Во избежание снижения точности расчетов авторы предлагают усовершенствовать методику I введением в граничные условия (1) поправки на теплообмен посредством ИК излучения по закону Стефана – Больцмана (методика II). В таком случае граничные условия на поверхности калибруемой модели грунта примут следующий вид:
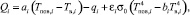 (2)
(2)
где Tпов,i – температура поверхности грунта или снега; σ0 – постоянная Стефана – Больцмана; b – коэффициент излучения атмосферы, зависящий от балла облачности, состава атмосферного воздуха, времени суток и изменяющийся в пределах от 0,69 до 0,89 [10]; ε – степень черноты подстилающей поверхности грунта, зависящая от типа поверхности, изменяющаяся в пределах от 0,89 до 0,99 [8].
Результаты оценки слагаемых, входящих в зависимость (2), для начальных условий: строительная площадка находится за полярным кругом; период года с минимальной продолжительностью светового дня; разница температуры поверхности снега и воздуха 2 К; температура воздуха 248 К; скорость ветра 3 м/с, приведены в табл. 1.
Таким образом, в граничных условиях методики I остается неучтенной от 24,4 % до 52,4 % тепловой энергии, передаваемой грунтом в атмосферу посредством ИК излучения.
Оценка значимости вклада ИК излучения в тепловой баланс грунтовых оснований криолитозоны и сравнение методик производились на базе 96 инженерно-геологических разведывательных скважин в ММГ с известными термометрическими данными (Пуровский район, ЯНАО, РФ). Основные отличия в процессе моделирования и его последовательность сведены в табл. 2.
Таблица 1
Оценочный расчет слагаемых конвективного и радиационного теплообмена
|
Основные виды теплообмена Последовательность расчета |
Конвективный тепловой поток ai (Tпов,i – Tв,i) |
Поток тепла от солнечной радиации qi |
Тепловой поток ИК излучения
|
|
Исходные данные |
ai = 30 Вт/(К∙м2) (Tпов,i – Tв,i) = 2 К |
qi = 0 Вт/м2 (полярная ночь) |
εi = 0,9 (для снега) σ0 = 5,67∙10–8 Вт/(м2 К4) Tв,i = 248 К Tпов,i = 250 К i = 0,69…0,89 |
|
Величина теплового потока, Вт⁄м2 |
60 |
0 |
66,14…27,53 |
|
Вклад в суммарный тепловой поток, % |
47,6…75,6 |
0 |
52,4…24,4 |
Таблица 2
Последовательность применения методик и их отличия
|
Наименование |
Методика I |
Методика II |
|
Этап I. Ввод исходных данных |
||
|
Исходные данные |
a; λ; δ; q |
a; λ; δ; q ε; b |
|
Этап II. Калибровка |
||
|
Калибруемый параметр |
a; λ |
b |
|
Основание для выбора параметра |
Регламент отсутствует |
|
|
Условие окончания калибровки |
Расчетная температура на глубине нулевых годовых амплитуд совпадает с результатами измерений в термометрических скважинах |
|
|
Этап III. Расчет ореола растепления |
||
|
Выполняемое действие |
1. Ввод стального газопровода в расчетную схему: Dн = 219 мм; hст = 6 мм; глубина заложения – 0,8 м; теплоизоляция – вспененный полистирол, 50 мм; tгаза = +17,5 °С. 2. Расчет ореола растепления в динамике |
|
Анализ результатов показал, что обе методики дают удовлетворительную сходимость с реальным распределением температур в грунте. Среднеквадратичные отклонения для методик I и II составляют соответственно 1,54 и 1,07 (рис. 2). Однако добиться таких результатов по методике I удается лишь путем калибровки коэффициента теплопроводности снега на величины, выходящие за рамки рекомендуемых почти на 100 % [9]. В то же время калибровка по методике II работает в пределах варьируемого параметра b от 0,7 до 0,85 в соответствии с рекомендациями [4].
Столь значительное изменение теплопроводности снега может привести к существенным отклонениям в результатах расчетов ореолов растепления во времени. На рис. 3 изображен график зависимости величины c от времени:
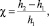 (3)
(3)
где h1 и h2 – расчетные величины протаивания ММГ под нижней образующей трубопровода, рассчитанные по методикам I и II соответственно.

Рис. 2. Результаты аппроксимации натурных данных сравниваемыми методиками
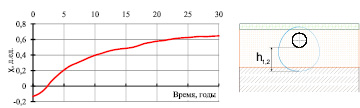
Рис. 3. Относительная разница ореолов растепления под трубопроводом в динамике
Значение c показывает относительную разницу в величинах протаивания ММГ в динамике, рассчитанных по двум моделям. Неучтённый методикой I тепловой поток, переносимый ИК излучением по закону Стефана – Больцмана привел к недооценке протаявшей зоны на 64 % за 30-летний период, а за 15-летний – на 50 %. Такая значительная недооценка однозначно приведет к развитию непредсказуемой просадки трубопровода в период его эксплуатации.
Выводы
С помощью численных методов проведен анализ существующей методики оценки теплового взаимодействия «горячих» трубопроводов с ММГ, положенной в основу действующей НТД. Обоснована необходимость в теплотехнических расчетах производить учет теплообмена грунта с атмосферой посредством ИК излучения. Выполнен сравнительный расчет тепловых полей в ММГ с применением усовершенствованной методики, показавший наличие весомых преимуществ предложенного подхода. Выполнено сравнение глубин протаивания под трубопроводом в динамике, показавшее значимую разницу конечных результатов. Калибровка модели грунта путем изменения коэффициента теплопроводности снега, выходящая за рамки физического смысла, приводит к значительному снижению расчетной величины ореола растепления вокруг трубопровода.
Рецензенты:Мерданов Ш.М., д.т.н., заведующий кафедрой «ТТС», ФГБОУ ВПО «Тюменский государственный нефтегазовый университет», г. Тюмень;
Тарасенко А.А., д.т.н., профессор кафедры «ТУР», ФГБОУ ВПО «Тюменский государственный нефтегазовый университет», г. Тюмень.
Работа поступила в редакцию 18.03.2015.