Исследование сложных технических систем проходит в условиях неопределенности, обусловленной, в частности, недостатком знаний об объекте исследований, а также возможностями измерений. Поэтому часто возникают нестандартные ситуации, для которых нет заранее известного набора действий, приводящих к нужной цели. Все задачи построения плана действий можно разбить на два типа, которым соответствуют различные модели искусственного интеллекта: поиск в пространстве состояний и в пространстве задач. Выбор представления зависит от знаний относительно объекта исследования. При отсутствии объективных вероятностных оценок выдвигаемых гипотез возможно использование субъективных знаний, формализованных с применением теории нечетких множеств [1, 6].
Дискретная модель активного эксперимента
Задача 1. Пусть относительно объекта исследований выдвинута группа из n – взаимоисключающих гипотез ε1, ..., εn, удовлетворяющих условию 
при l ≠ k. Также определено множество допустимых экспериментов Q = {q1...qn} по верификации этих гипотез и соответствующие стоимости их проведения C = {c1...cn}. Требуется оптимизировать процесс экспериментального подтверждения одной из гипотез εk.
Введем в рассмотрение дискретное пространство состояний эксперимента S. Поставим k-й гипотезе в соответствие упорядоченную последовательность (01, 02, ..., 1k, ..., 0n) пространства 
. Тогда 
отражает исходную неопределенность в виде группы гипотез ε1, ..., εn и En, как возможное поле действия эксперимента. Принимаем S0 за начальное состояние процесса исследования.
Эксперимент qj связан с подачей управляющих воздействий 
на экспериментальную установку, измерением параметров 
и результатом обработки информации Wk
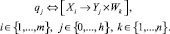(1)
Эту совокупность «атомарных» действий будем считать элементарным экспериментом.
В процессе проведения эксперимента qj, отбрасывая k-ую гипотезу, мы сужаем поле действия эксперимента на грань n-мерного куба, которая сама является кубом. Следовательно, промежуточному состоянию Sj соответствует набор (a1, ..., an) ∈ En, ak = 0 при отбрасывании гипотезы, ak = 1 – в противном. Конечное состояние представлено набором (ek, ek), где (ek = (01, 02, ..., 1k, ..., 0n) – «1» на k-меcте, соответствует принятию εk.
В результате имеем пространство состояний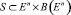 
как подмножество множества всех пар вершин n и подпространств в En. Последовательное выполнение экспериментов q0, q1, ..., qh ∈ Q интерпретируется как композиция o отображений 
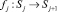. Таким образом, формализована алгебраическая система 
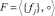со свойствами замкнутости, ассоциативности, идемпотентности, необратимости. Выбор возможной последовательности будем оценивать функцией качества 
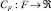. В итоге получена дискретная модель активного эксперимента в пространстве S:
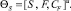(2)
На начальном этапе эксперимента отсутствуют знания об исходном распределении вероятностей гипотез, поэтому положим
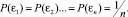
Если в результате qj-эксперимента отвергнута гипотеза εk, (произошло событие Bk), то вследствие теоремы Байеса получаем апостериорные вероятности гипотез εj, j ≠ k:
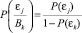(3)
при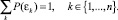 
Такой подход позволит сформировать в дальнейшем вероятностную модель эксперимента.
Вероятностная модель активного эксперимента
Возможно, что нам априори известны вероятности гипотез P(εk) из ранее набранной статистики. Это дает возможность точечной оценки вероятностей гипотез P(εk).
Задача 2. Пусть относительно объекта исследований выдвинута полная группа из n-попарно несовместных гипотез εk с вероятностями P(εk), причем
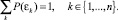(4)
Также определено множество допустимых экспериментов Q = {q1...qn} по верификации этих гипотез и соответствующие стоимости их проведения C = {c1...cn}. Требуется оптимизировать процесс экспериментального подтверждения одной из гипотез εk.
Верификацию гипотез εk можно вести согласно вероятностной модели активного эксперимента, которая имеет вид [1, 3]
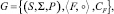(5)
где (S, Σ, P) – вероятностное пространство с соответствующей σ-алгеброй Σ.
Пространство S связано с распределением Р, которое образует вероятностный симплекс
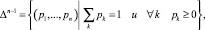
натянутым на единичные векторы ek (рис. 1).
Распределение вероятностей гипотез, представленное упорядоченной n-й, будет точкой S, лежащей на вероятностном симплексе. Знание вероятностей P(εk) позволяет нам вести оптимизацию по такому критерию, как энтропия эксперимента или энергозатраты [2].
Для реализации вероятностной модели эксперимента необходимо знание исходного распределения вероятностей P(ε1), P(ε2), ..., P(εn). При отсутствии такой оценки на ранних стадиях эксперимента применим лингво-численную оценку с помощью высказываний, например: вероятность гипотезы составляет «около или близко к 0,5».
Фаззификация задачи эксперимента
Точечные оценки вероятностей реально часто являются недосягаемыми в силу различных ограничений, поэтому вводим нечеткие значения оценки вероятностей. Для этого ослабим условия задачи 1 и вместо точечной оценки P(ε1), P(ε2), ..., P(εn) введем эмпирическую или теоретическую оценку степени принадлежности вероятности k-гипотезы μ(xk) ∈ Φ, k ∈ {1, ..., n}, где Φ – множество выпуклых функций принадлежности.
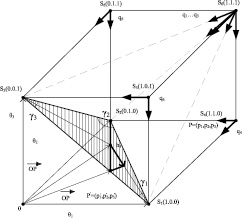
Рис. 1. Пространство S с вероятностным симплексом Р
Задача 2. Пусть относительно объекта исследований выдвинута группа из n-гипотез ε1, ..., εn с оценками их вероятностей имеющимися функциями принадлежности μ(xk) ∈ Φ, k ∈ {1, ..., n}. Также определено множество допустимых экспериментов Q = {q1...qn} по верификации гипотез и стоимости их проведения C = {c1...cn}. Требуется оптимизировать процесс экспериментального подтверждения одной из гипотез εk.
Отличием данного подхода является то, что условие несовместности гипотез и ограничение (4) может не выполняться. Используя априорные знания о неопределенности оценок (измерения), проводим фаззификацию задачи эксперимента.
Отразим исходную неопределенность значений оцениваемой (измеряемой) величины нечеткими числами (ℜ, μ(x)) с симметричными гауссовскими функциями принадлежности
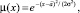(6)
где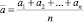 
– усредненная оценка значений измеряемой величины, данная через n-измерений или оценок экспертов; σ – соответствующее среднеквадратичное отклонение оценки.
Нетрудно видеть, что определенная нами функция μ(x) нечеткого числа удовлетворяет условиям непрерывности, нормальности, выпуклости [6].
Однако прямое использование нечетких чисел с функциями принадлежности вида (6) ведет к значительным вычислительным трудностям. На основании этого представим функции μ(x) в упрощенном модифицированном LR-формате, который выбирается из условия минимума отклонения от функции (6). В данной работе мы предлагаем использовать унимодальные нечеткие FN-числа (треугольные), так как они более адекватно оценивают высказывания типа «вероятность гипотезы приблизительно равна 0,5». Замена функции принадлежности показана на рис. 2.
Аналитически μk(x) записывается следующим образом:
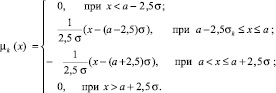(7)
Для математической модели обработки неопределенности, появляющейся при измерении (оценке) параметров, мы предлагаем арифметику FN-чисел [4].
Арифметика нечетких FN-чисел
Пусть a – усредненная оценка значений измеряемой величины; σ – среднеквадратичное отклонение. Определим нечеткое число парой
,
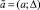где 2Δ = 5σ – ширина интервала.
Определение 1. Нечеткие числа, функция принадлежности которых имеет график в форме равнобедренного треугольника (трапеции), будем называть нечеткими естественными (Fuzzy Naturale) числами и записывать в виде (a; Δ).
В основе операций сложения и умножения лежит расширенная бинарная арифметическая операция o:
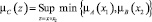[6].
Как известно, операции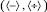 
выражаются через операции 
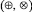посредством симметрии и инверсии соответственно, а операция логарифмирования получается естественным образом:
, a > 0, a > Δ. (8)
Определение 2. Нечетким множеством оценок Ak назовем
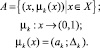(9)
На множестве A определена Ψ-арифметика нечетких чисел
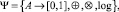
что позволяет оперировать с FN-числами в рамках поставленной задачи.
Нечеткая модель эксперимента
Пусть S дискретное пространство состояний, {qj} – множество элементарных экспериментов. Ввиду неопределенности измерений и результатов обработки эксперимент свяжем с отображением нечетких множеств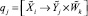 
. Этому отображению соответствует нечеткий оператор 
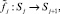причем 
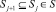. В этом случае 
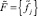определяет нечеткое отношение 
на множестве S. Отношение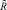 
можно отнести к нечетким порядковым отношениям, так как не имеет контуров, обладает свойствами антисимметричности, транзитивности и антирефлексивности [5, 6]. Любому антисимметричному нечеткому отношению 
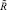можно поставить в соответствие один (и только один) обычный антисимметричный граф G. Такое отношение можно представить на плоскости взвешенным графом с матрицей отношений 
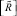, в котором каждая пара вершин (Si, Sj) соeдиняется стрелкой с весом 
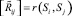(рис. 3).
Данные положения представлены нечеткой моделью эксперимента
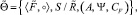(10)
где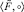 
– алгебраическая система с одной определяющей операцией; 
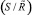– дискретное пространство S с заданным отношением 
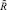; (A, Ψ, CF) – Ψ-арифметика FN-чисел на множестве оценок A с функцией стоимости CF.
В качестве C(fj) могут использоваться различные критерии эксперимента, например стоимость, время, сложность, энергозатраты [5]. В последнее время наблюдается интерес к применению энтропии для оценки степени неопределенности систем.
Оптимизация эксперимента по энтропии
Будем учитывать неопределенности, обусловленные как вероятностным (случайным) характером эксперимента, так и нечеткостью наших знаний об объекте исследований. Основываясь на приведенном выше анализе, предлагаем следующее определение общей энтропии эксперимента.
Определение 3. Общей энтропией эксперимента назовем композицию двух составляющих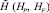 
, где HP обусловлена случайным характером эксперимента, определяется по формуле Шеннона
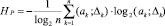. (11)
Нечеткая составляющая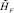 
носит вычислительный характер и связана с площадью П, соответствующей FN-числу
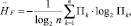(12)
где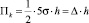 
– площадь треугольника, ограниченная функцией принадлежности μ(xk) и осью Ox, h – высота (рис. 2).
Рис. 2. Переход μ(x) от нормального закона к унимодальному LR-формату
Рис. 3. Нечеткое отношение 
на множестве S
При проведении эксперимента HP → 0, а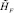 
возрастает, так как имеет вычислительную природу (при увеличении количества вычислений ошибка тоже растет). В результате у нас есть две разнонаправленные величины. При этом получим задачу многокритериальной оптимизации, которую можем свести к задаче оптимизации с одной скалярной целевой функцией. Используем функцию скаляризации Чебышева
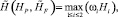(13)
ωi – вес i-критерия.
Правило 1. Максимум приращения информации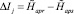 
на j-шаге определяет направление поиска, то есть выбор эксперимента qj из априорного набора Q:
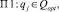
если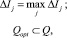 
где Qopt – набор экспериментов, входящих в оптимальный вариант проведения эксперимента; Hapr – априорная энтропия; Haps – энтропия после проведения j-эксперимента определяется по формуле (3), в которой вместо pk подставляются значения (ak, Δk). Таким образом, можно вести оптимизацию эксперимента по нечеткой энтропии с контролем точности вычислений. Рассмотренная энтропия является удобным инструментом анализа неопределенности в задачах принятия решения, диагностики, управления и оптимизации, особенно на ранних стадиях эксперимента.
Заключение
Проблемно-ориентированный подход к интеллектуализации эксперимента позволяет выбрать наилучшее представление и формулировать задачу эксперимента в зависимости от уровня знаний об объекте исследований.
Если нам известны вероятности гипотез, то можно использовать в качестве критерия информационную энтропию Шеннона (оптимизация по ΔI) или вести поиск решения проблемы эксперимента по энергозатратам [2, 3].
Если у нас нет достаточной статистической базы для формирования вероятностной модели, то в рамках нечеткого подхода можно формулировать проблему эксперимента при недостатке знаний об объекте исследований. Это позволяет оценить и выбрать направление поиска в условиях, когда объект эксперимента и внешняя среда эволюционируют [5, 6].
Представление общей энтропии в виде вероятностной и нечеткой составляющих позволяет осуществить переход от нечеткой модели к вероятностной по мере приобретения знаний, а также накапливать информацию о неопределенности при обработке результатов эксперимента и выбирать приемлемую точность эксперимента.
Рецензенты:Чаткин М.Н., д.т.н., профессор, ректор, ФГБОУ «Мордовский институт переподготовки кадров агробизнеса», г. Саранск;
Щенников В.Н., д.ф.-м.н., профессор, ФГБОУ ВПО «МГУ им. Н.П. Огарева, г. Саранск.
Работа поступила в редакцию 18.03.2015.