В практике обработки результатов испытаний образцов на циклическую прочность с целью построения кривой усталости (кривой Велера) в настоящее время наибольшее распространение получили регрессионные зависимости [2], являющиеся линейными в системе координат log N – σ, где N – число циклов деформирования, σ – максимальная амплитуда напряжения, возникающая в месте разрушения образца. Эти зависимости в рамках статистических моделей рассеивание механических и усталостных свойств материала учитывают, однако какого-либо физического наполнения не имеют. Обеспечение требуемой долговечности и надежности циклически нагружаемых изделий с заданной вероятностью неразрушения связано с необходимостью использования более сложных моделей, отражающих процесс накопления усталостных повреждений в изделиях. Именно такие модели разработаны в кинетической теории механической усталости [1]. Наиболее важным практическим значением этой теории является возможность построения кривых усталости, соответствующих различной величине поврежденности материала (D): от D = D0 ≥ 0, характеризующей начальное повреждение материала детали, которое имеет место еще до начала ее циклического деформирования, вплоть до предельной величины D = Dk ≤ 1, соответствующей разрушению детали (образца) вследствие накопленных усталостных повреждений.
Целью настоящей работы является построение алгоритмов обработки данных малоцикловых испытаний (совокупности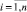 
значений напряжений σi и числа циклов Ni до разрушения образцов) на основе полуэмпирических моделей, разработанных в рамках кинетической теории усталости, а также методики расчета границ доверительных интервалов кривой малоцикловой усталости.
Математическая модель кривой малоцикловой усталости
В работе [1] для описания кривой многоцикловой усталости получено выражение
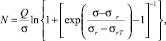(1)
где N – число циклов нагружения; σ – максимальное напряжение цикла; Q – коэффициент выносливости; σr – предел выносливости детали при коэффициенте асимметрии цикла r; σrT – циклический предел текучести (ниже его уровня следы пластической деформации даже после нескольких миллионов циклов нагружения отсутствуют).
Определение значений параметров σr, σrT и Q зависимости (1) на основе имеющейся совокупности данных разрушения образцов σi, Ni,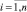 
выполняется путем минимизации функции [4, 3]:
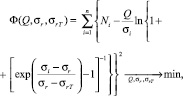(2)
построенной в соответствии с методом наименьших квадратов.
Математическое описание кривой усталости в малоцикловой области (N ≤ 105) представлено в работе [1] выражением
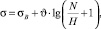(3)
где σB – предел прочности материала; ϑ – угол наклона кривой усталости в системе координат log N – σ; H – число циклов деформирования до верхней точки перегиба кривой малоцикловой усталости, рассчитываемое по выражению (1) при σ = σB:
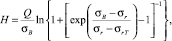(4)
в котором коэффициент Q описывается зависимостью
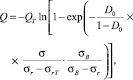(5)
где QT – коэффициент, характеризующий сопротивление детали росту усталостных трещин.
В работе [1] отмечено, что величины D0 и QT могут быть определены на основе: зафиксированных длин усталостных трещин, измерении поврежденных площадей испытуемых деталей, путем расчета моментов инерции поврежденных сечений деталей. Однако в реальных условиях испытаний получение такой информации часто весьма затруднено, а в подавляющем большинстве случаев просто невозможно. Тем не менее знание начального D0 и предельного значения параметра Dk позволяет при заданной величине действующего напряжения σ и числа циклов нагружения N оценить достигнутый уровень текущей поврежденности материала D и в конечном итоге, реализовать процедуру расчета остаточной долговечности детали (образца).
Для кривой многоцикловой усталости (1) задача определения величин D0 и QT на основе данных усталостных испытаний образцов σi, Ni,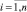 
впервые решена в работе [4]. В настоящей работе подобная задача решается для кривой малоцикловой усталости (3).
Воспользуемся зависимостью (5), которую преобразуем следующим образом:
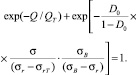(6)
После решения задачи (2) значения параметров σr, σrT и Q на основе имеющейся совокупности данных усталостных испытаний σi, Ni,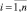 
определены: 
, 
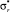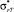и Q*. В этом случае выражение (6) получает вид
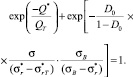(7)
Зададимся средним значением предела прочности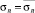 
. Тогда в уравнении (7) неизвестными являются только два параметра: D0 и QT. Для их определения воспользуемся следующим приемом. Поскольку величина D0 характеризует поврежденность материала в исходном состоянии, ее значение от величины действующего напряжения (σ) при деформировании образца не зависит. То есть D0 является постоянной для всего диапазона изменения напряжений σ. Если, в дополнение к отмеченному, предположить, что и коэффициент QT в диапазоне изменения напряжений 
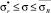также является величиной постоянной, то для расчета D0 и QT войдем в уравнение (7) дважды: при напряжени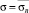и 
и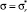 
. В результате получим
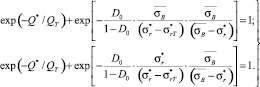(8)
Решая систему (8) двух трансцендентных относительно D0 и QT уравнений с использованием численных методов, определим искомые значения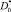 
и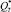 
.
Принимая во внимание, что текущая поврежденность материала описывается выражением (5) при замене D0 на D, и учитывая результат решения системы (8), математическую модель кривой малоцикловой усталости (4) преобразуем к виду
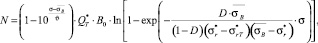(9)
где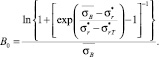 
Рис. 1. Разрушенные образцы гибких труб
Обработка данных малоцикловых испытаний образцов
На основе модели (9) осуществим обработку данных малоцикловых испытаний образцов из гибкой трубы HS-80. В результате растяжения образцов гибкой трубы на разрывной машине до разрушения (рис. 1) определено значение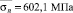 
. В процессе малоциклового деформирования вырезанных из гибкой трубы экспериментальных образцов прямоугольной формы на стенде (рис. 2) в условиях жесткого нагружения, получена совокупность данных Ni, σi, 
. Обработка их в соответствии с вышеизложенной методикой позволила установить параметры модели (9): ϑ = –121,811;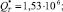 
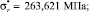
Рис. 2. Стенд для испытаний образцов
Рис. 3. Кривые малоцикловой усталости с различной величиной поврежденности материала (гибкая труба HS-80)
На рис. 3 в координатах log N – σ представлены экспериментальные точки и ряд кривых усталости с величиной поврежденности:
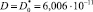(толстая линия);
10–7; 10–5; 10–4; 10–3.
Анализируя рис. 3, нетрудно видеть, что при D = D0 и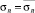 
выражение (9) описывает кривую усталости (толстая линия), соответствующую 50 % вероятности разрушения образцов. По мере увеличения поврежденности материала кривая усталости смещается влево, в область с меньшей долговечностью образцов.
Математическая модель кривой малоцикловой усталости в виде (9) позволяет не только определять снижение числа циклов деформирования образцов до разрушения в зависимости от накопленного усталостного повреждения, но и решать задачу определения эквивалентного по повреждающему воздействию напряжения при заданном блоке изменения нагрузки. Методика решения этой задачи, разработанная на основе построенной математической модели (9), представлена в работе [5].
Заключение
На базе кинетической теории механической усталости построена математическая модель кривой Велера для малоцикловой области испытаний, отражающая процесс накопления усталостных повреждений в ходе циклического деформирования образцов. На основе полученных в ходе испытаний образцов на малоцикловую усталость экспериментальных данных разработаны алгоритмы определения параметров модели. С использованием разработанной модели обработаны данные малоцикловых усталостных испытаний образцов из гибкой трубы.
Рецензенты:
Лопатин Б.А., д.т.н., профессор, зав. кафедрой «Техническая механика», ФГБОУ ВПО «Южно-Уральский государственный университет» (национальный исследовательский университет), филиал ЮУрГУ, г. Златоуст;
Трубачёв Е.С., д.т.н., профессор, и.о. зав. кафедрой «Конструкторско-технологическая подготовка машиностроительных производств», ФГБОУ ВПО «Ижевский государственный технический университет им. М.Т. Калашникова», г. Ижевск.
Работа поступила в редакцию 09.02.2015.