Одной из важнейших проблем организации космических миссий для изучения Марса и других планет Солнечной системы является выработка и обоснование требований к энергетическим и массово-габаритным параметрам создаваемых перспективных космических аппаратов (КА). Это обуславливается необходимостью учета различных факторов, влияющих на проектный облик и массовые характеристики автоматических и пилотируемых КА.
Все это в сочетании с необходимостью решения широкого спектра научно-исследовательских целевых задач предопределяет исключительную важность проблемы поиска путей увеличения доли научной аппаратуры в общем весовом балансе КА. Существенным резервом в решении этой проблемы является организация движения КА по энергетически оптимальным траекториям.
Одно из перспективных направлений оптимизации управления КА состоит в разработке аналитических методов решения вариационных задач. Кроме сокращения затрат расчетного времени это дает и другие преимущества. Форма решения получается более наглядной, что облегчает проведение сравнительного анализа различных вариантов. Оптимальные законы управления могут иметь вид явных зависимостей от начальных условий и параметров системы, что позволяет оценить степень влияния той или иной характеристики на управляющие параметры.
Постановка задачи
Движение КА в атмосфере по аналогии с работами [1, 2, 6] описывается системой дифференциальных уравнений:
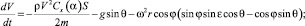
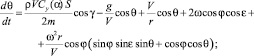
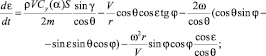(1)
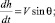
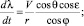
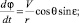
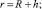
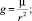
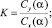
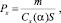
где V – скорость КА; θ – траекторный угол; ε – курсовой угол; r – радиус-вектор положения КА; λ и φ – долгота и широта подспутниковых точек КА; m – масса КА; t – время; ρ – плотность атмосферы; Cx и Cy – аэродинамические коэффициенты лобового сопротивления и подъемной силы; R – радиус планеты; h – высота полета; g – ускорение силы тяжести; μ – гравитационный параметр; K – аэродинамическое качество; S – площадь миделева сечения; Px – приведенная нагрузка на лобовую поверхность КА; α – угол атаки; γ – угол крена.
Значения управляющих параметров α и γ могут изменяться в пределах
0 ≤ α ≤ αmax; –π ≤ γ ≤ π. (2)
Для различных моделей атмосферы Марса плотность ρ в зависимости от высоты полета КА определяется в соответствии с методикой, изложенной в работах [5].
Значения коэффициентов Cx и Cy зависят от форм КА. Рассматривались аппараты сегментно-конической формы с максимальным аэродинамическим качеством Kmax = 0,34; типа «несущий корпус» с Kmax = 1,5; самолетной формы с Kmax = 2,4. Для таких форм зависимости Cx, Cy и K от угла атаки α приведены, в частности, в работе [2].
Будем считать, что начальная точка траектории t = t0 соответствует моменту входа КА в атмосферу Марса. При этом все значения начальных параметров КА известны:
xi(t0) = xi0, i = 1, 2, …, 6. (3)
В конечной точке траектории t = tk (вылет КА из атмосферы) известно значение радиуса-вектора КА:
rk = R + hатм, (4)
здесь hатм = 100 км – высота условной границы атмосферы Марса.
При выведении на орбиту должно выполняться соотношение, связывающее значения конечных параметров Vk, θk и rk в инерциальной системе координат с заданным радиусом rα:
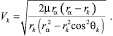(5)
В качестве критерия оптимальности будем использовать максимум скорости КА в конечной точке траекторий J = Vk = max, что обеспечивает минимум потребных энергозатрат при формировании орбиты ИСМ [2].
Задача максимизации коридора входа КА в атмосферу сводится к решению двух независимых вариационных задач о нахождении минимума и максимума высот условного перицентра, характеризующих верхнюю и нижнюю границы коридора входа:
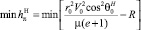
или
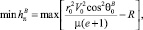
где e – эксцентриситет полетной орбиты.
Итак, сформулируем задачу оптимального управления КА в общем виде: для процессов, описываемых системой дифференциальных уравнений (1), требуется определить программу управления углами α(t) и γ(t), обеспечивающую экстремум функционала J при ограничениях (2) и краевых условиях (3)–(5).
Метод расчета оптимальных траекторий
При разработке аналитического метода использовались общеизвестные допущения, обоснованные в ряде работ [2, 6, 8]:
h ≪ R; ρ = ρ0exp(–βh); Fk + Fц ≪ Fгр ≪ Fа,
где Fk, Fц, Fгр, Fа – кориолисова, центробежная, гравитационная и аэродинамическая силы соответственно; ρ0 – плотность атмосферы на поверхности планеты; β – логарифмический коэффициент изменения плотности атмосферы от высоты.
Введем замены переменных
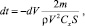z = –ln V.
В результате получим систему, не содержащую в явном виде аргумент z:
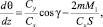
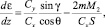(6)
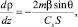
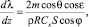
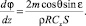
Следуя [2], будем считать M1 и M2 кусочно-постоянными функциями. Отметим, что при движении КА в атмосфере аргумент z возрастает.
Для определения оптимальных законов управления параметрами α и γ воспользуемся принципом максимума Понтрягина [4]. При z0 ≥ z ≥ zk гамильтониан и система уравнений сопряженных переменных запишутся следующим образом:
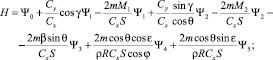(7)
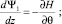
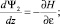(8)
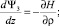
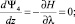
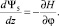
При использовании в качестве аргумента управления параметра z, согласно [4], в систему (6) вводится дополнительное дифференциальное уравнение dz/dz = 1. В связи с тем, что правые части этой системы не содержат в явном виде аргумент z, соответствующее уравнение для сопряженной переменной Ψ0 определяется формулой
dΨ0/dz = 0.
Законы изменения α и γ при оптимальном управлении определяются в результате решения системы ∂H⁄∂α = 0, ∂H⁄∂γ = 0, и их можно записать в виде
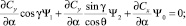
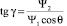. (9)
Следует отметить, что найденная структура управления соответствует структуре, обоснованной в работе [2]: в процессе полета КА в атмосфере осуществляется одноразовое переключение угла крена γ с нулевого значения на γ = π.
Граничные условия для сопряженных переменных Ψi (i = 0, 1, ..., 5) при z = z0 и z = zk получим из условия трансверсальности [3]
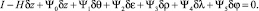(10)
Таким образом, для определения оптимальных траекторий необходимо решить уравнения (9) с учетом дифференциальных связей (6)–(8) и краевых условий (10).
Алгоритм расчета управляющих параметров
Для определения управляющих параметров разработан ускоренный вычислительный алгоритм, базирующийся на прогнозировании оставшихся участков полета на основе измерений текущего положения КА.
Зависимость между углом θ и аргументом z может быть определена на основе интегрирования первого уравнения системы (6):
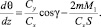
Окончательно запишем
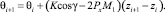(11)
Преобразуя первое уравнение системы (6), получим
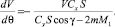
После его интегрирования на интервалах кусочного постоянства функции M1(ti, ti+1) запишем формулу
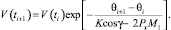(12)
Поделив второе уравнение системы (6) на третье и учитывая указанное допущение об экспоненциальном характере изменения плотности атмосферы от высоты, получим дифференциальное уравнение с разделяющимися переменными:
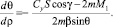
Интегрируя его в интервалах (ti, ti+1), запишем формулу связи между текущими значениями высоты полета h и траекторного угла θ:
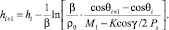(13)
Таким образом, с использованием рекуррентных соотношений (11)–(13) могут быть рассчитаны траектории движения КА в атмосфере с заданными значениями углов крена и атаки от момента измерений значений Vi, θi до выхода КА из атмосферы.
Определив величины Vк, θк в инерциальной системе координат и вычислив значения кеплеровских интегралов энергии C1 и площадей C2:
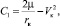
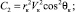
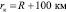
получим формулу для расчета высоты и скорости КА в апогее переходной орбиты:
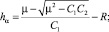
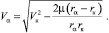(14)
Далее на основе рекуррентных зависимостей (11)–(13) опишем алгоритм определения управляющих параметров, при которых обеспечивается максимум скорости вылета КА из атмосферы и, соответственно, скорости аппарата в апогее переходной орбиты.
Вход КА в атмосферу осуществляется с нулевым углом крена и углом атаки α*, соответствующим максимальному значению аэродинамического качества. Предполагается, что с интервалом ∆t = ti+1 – ti проводится измерение текущих значений скорости Vi, угла θi и высоты полета hi. Для каждого из моментов измерений ti по рекуррентным соотношениям (11)–(13) определяются значения скорости Vк и траекторного угла θк при вылете КА из атмосферы для двух различных режимов полета: с γ = 0, α = α* и γ = π, α = α*. С помощью формулы (14) определяются значения высот апогея переходных орбит hα1 (γ = 0) и hα2 (γ = π).
Сразу после входа КА в атмосфере планеты будут справедливы соотношения hα1 > hαзад и hα2 < hαзад, где hαзад – заданная высота апогея формируемой орбиты. Затем, в процессе полета КА с нулевым значением угла крена высота hα2 будет возрастать, достигая в определенный момент времени t* заданной высоты hαзад. Начиная с этого момента представляется необходимым уменьшать угол атаки α, обеспечивая тем самым снижение действующей на КА подъемной силы и его полет в более плотных слоях атмосферы. Такое управление углом атаки сначала обеспечивает снижение интенсивности роста высоты hα2, а затем по достижении некоторого угла α′ и прекращение роста hα2. После этого происходит разворот КА по углу атаки, что соответствует возрастанию подъемной силы и аэродинамического качества. В результате высота hα2 начинает уменьшаться, оставаясь в пределах hα2min < hα2 < hα2max и приближаясь к нижней границе. В момент достижения hα2 заданной высоты апогея hαзад угол атаки α устанавливается равным α*, а угол крена γ принимает значение, равное π. При таком режиме полета обеспечиваются необходимые условия вылета КА из атмосферы и достижение заданной высоты апогея hα2.
Таким образом, разработан алгоритм расчета оптимального управления КА углами крена и атаки, обеспечивающими максимальную скорость вылета аппарата из атмосферы при последующем формировании спутниковых орбит с заданными высотами апогея.
Результаты применения алгоритма
Анализ результатов численного и аналитического решений вариационных задач показал их полное качественное совпадение. Так, в процессе движения КА в атмосфере угол крена изменяется от γ0 ≈ 3–8° до γ ≈ 172–177° (при аналитическом решении угол γ меняется от 0 до 180°). Угол атаки α при входе КА в атмосферу принимает значение α*, соответствующее значению Kmax, далее происходит увеличение α до значения, соответствующего максимуму коэффициента Cx, а затем α вновь снижается до α* (при аналитическом решении также установлен максимум угла атаки в процессе полета КА).
При формировании круговой орбиты высотой H = 500 км для КА, обладающего аэродинамическим качеством K = 0,43 и приведенной нагрузкой Px = 300 кг/м2, учитывая возможный разброс параметров атмосферы, максимальный коридор входа ∆hπ составляет ±25 км. При этом, верхняя граница hπmax = 30 км – соответствует наименее плотной модели атмосферы, а нижняя граница hπmin = –20 км – наиболее плотной модели. Значения реализуемого коридора входа превосходит величину навигационного коридора (при использовании автономных систем навигации КА 
[2]), что позволяет сделать вывод о возможности осуществления предлагаемой схемы выведения.
Показано, что потребные энергозатраты ∆V существенно зависят от высоты условного перицентра. Причем уменьшение высот hπ от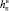 
сначала приводит к незначительному увеличению энергозатрат ∆V, а затем – с приближением hπ к нижней границе коридора 
– происходит интенсивное возрастание ∆V (рисунок).
Так, при изменении высоты hπ от 30 до –10 км энергозатраты ∆V практически не меняются и составляют ∆V ≈ 145 м/с, дальнейшее снижение hπ до –20 км приводит к росту ∆V до 280 м/с (H = 500 км). Зависимости ∆V (hπ) имеют аналогичный характер и для случаев формирования более высоких орбит. При этом значения ∆V увеличиваются с ростом высоты H. Так, при H = 2000 км энергозатраты ∆V в зависимости от значений hπ составляют 310–480 м/с, а для H = 5000 км – ∆V ≈ 570–610 м/с. Представленные данные показывают, что энергетически оптимальным является осуществление входа КА в атмосферу вблизи верхней границы коридора.
В целом для широкого диапазона исходных данных и проектно-баллистических характеристик потребные энергозатраты ∆V не превышают 650 м/с, а при входе КА в атмосферу вблизи верхних границ коридора 
и формировании орбит ИСМ с высотами H не более 500 км энергозатраты составляют ~140–150 м/с.
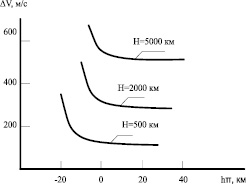
Зависимости потребных энергетических затрат ∆V от высоты условного перицентра траектории входа КА в атмосферу hπ при выведении на круговые орбиты ИСМ с высотами H (Kmax = 0,34; Px = m/CxS = 300 кг/м2).
Для сравнения в случае применения традиционной ракетодинамической схемы формирования спутниковых орбит [7], потребные энергозатраты достигают 2,5–4 км/с, что в 6–10 раз больше, чем при использовании рассмотренной комбинированной схемы.
Заключение
Рассмотрена комбинированная схема выведения космического аппарата на орбиту искусственного спутника Марса, предусматривающая предварительное аэродинамическое торможение КА в атмосфере, перевод на переходную эллиптическую орбиту и подачу разгонного импульса в ее апоцентре.
Разработан новый алгоритм решения задач управления КА на основе введения ряда допущений и преобразования систем уравнений движения и сопряженных переменных.
Показано, что для КА, располагающих аэродинамическим качеством Kmax ≥ 0,3, коридор входа КА в атмосферу превосходит навигационный коридор, что обеспечивает принципиальную возможность осуществления предлагаемой схемы управления.
Для случаев входа КА в атмосферу вблизи верхней границы коридора потребные энергетические затраты на формирование орбиты ИСМ ~ на порядок меньше, чем при реализации ракетодинамической схемы перевода КА с подлетной гиперболической траектории на заданную орбиту.
Рецензенты:
Лаврентьев В.Г., д.т.н., заместитель начальника отдела, ФГУП «Центральный научно-исследовательский институт машиностроения», г. Королев;
Лобачев В.И., д.т.н., профессор, заместитель начальника Центра управления полетами, ФГУП «Центральный научно–исследовательский институт машиностроения», г. Королев.
Работа поступила в редакцию 09.02.2015.