Рельсотрон – импульсный электродный ускоритель масс, состоящий из двух параллельных электропроводных шин, вдоль которых движется электропроводная масса (снаряд или плазма) [8]. Принцип работы основан на превращении электрической энергии в кинетическую энергию снаряда. С изготовлением рельсотрона связан ряд серьёзных проблем: импульс должен быть настолько мощным и резким, чтобы снаряд не успел бы испариться и разлететься, но возникла бы ускоряющая сила, разгоняющая его вперед. Поэтому материал снаряда и рельс должен обладать как можно более высокой проводимостью, снаряд как можно меньшей массой, а источник тока как можно большей мощностью и меньшей индуктивностью [5, 6].
Количественное определение указанных характеристик позволит глубже познать особенности физических процессов, происходящих в рельсотроне, а также многих электрофизических устройств, работающих в импульсном электромагнитном поле (ЭМП), когда при проектировании и оптимизации их работы возникает необходимость расчета параметров с учетом проникновения (диффузии) ЭМП в массивные проводники [7]. В работе предложена математическая модель для исследования процессов, происходящих в рельсотроне, и алгоритм расчета электрических параметров на основе расчета энергии электромагнитного поля.
Необходимо учесть, что распределение плотности тока по сечению рельсотрона неравномерно. Форма импульса тока – несинусоидальна. Поэтому при расчёте распределения плотности тока по сечению проводника применялся принцип наложения. В соответствии с принципом суперпозиции (наложения) расчёт можно вести для каждой гармоники отдельно. Рассмотрим несинусоидальный импульс тока как ток от действия пяти гармоник, амплитуды и начальные фазы которых определяются с использованием разложения в ряд Фурье. Гармониками выше пятой можно пренебречь, степень приближения к исходному импульсу можно оценить, используя теорему Парсеваля [7]:
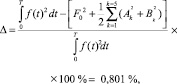
где k – номер гармоники; F0, Ak,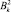 
– постоянная составляющая, амплитуды косинусной и синусной составляющей k-й гармоники; f(t) – исследуемая функция; T – период.
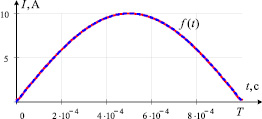
Качественно приближения к исходному импульсу демонстрирует рис. 1. Сплошной линией изображена исходная функция, пунктирной – полученная в результате сложения пяти гармоник и постоянной составляющей, Im – амплитуда однополярного синусоидального импульса. Определим частотный спектр импульса. Для этого разложим импульс в ряд Фурье, определив коэффициенты разложения Ak, k = 0, ..., N. Для определения коэффициентов использовалась стандартная программа быстрого преобразования Фурье (FFT) программно-интегрированной среды MathCAD. Далее функция представлялась в виде ряда:
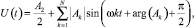
где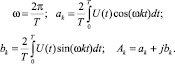 
Спектр и результат восстановления функции по коэффициентам представлены ниже.
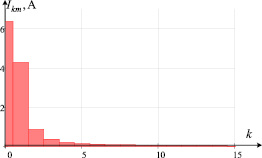
Число коэффициентов разложения бралось N = 15. Из спектра импульса видно, что, начиная с 5 гармоники, относительный вклад высших гармоник в импульсе не превышает 5 %.
а
б
Рис. 1. Однополярный импульс: а – исходный импульс показан сплошной линией, пунктирной показан импульс, полученный в среде MathCAD; б – амплитудно-частотный спектр
Зная геометрические размеры рельсотрона, решаем уравнение электрического поля в проводнике (1) численным методом интегрирования дифференциальных уравнений в частных производных путем сведения их к уравнениям в конечных разностях [2, 4].
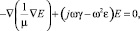(1)
где E – напряженность электрического поля; μ = 4π∙10–7 – магнитная постоянная; γ = 57∙106 1/(Ом∙м) – удельная проводимость (для меди); ε = 8,86∙10–12 – электрическая постоянная; ω – угловая частота.
В проводящей среде даже при очень высоких частотах произведение ω2ε много меньше ωγ. Поэтому с большой степенью точности слагаемым ω2εE можно пренебречь.
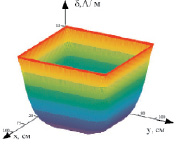
Программная среда pdetool математического пакета Matlab позволяет найти решения дифференциальных уравнений в двумерных областях методом конечных элементов [1, 3]. В результате получаем массив распределения плотности тока по поперечному сечению рельсотрона. Графики распределения плотности тока по сечению даны на рис. 2. С увеличением частоты плотность тока возрастает к периферии рельсотрона. Электрическое поле определяется через плотность 
тока проводимость γ
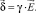
Зная распределение тока по сечению, можно вычислить напряженности поля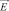 
и 
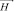. Электрическое поле определяется через плотность 
тока проводимость γ.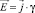 
.
Об адекватности метода можно судить по совпадению полученных результатов с известным расчётом распределения плотности тока круглого проводника с использованием функций Бесселя [2, с. 168–170], на рис. 3, б – пунктирная линия, с использованием среды pdetool математического пакета Matlab – сплошная линия.
Электрическое поле и магнитное связаны уравнением Максвелла.
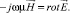
Откуда определяется напряженность магнитного поля с учётом того, что у вектора напряжённости электрического поля присутствует только z-я составляющая (ось z направим вдоль оси рельсотрона (рис. 4))
.
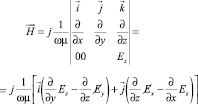Известно, что операция дифференцирования является некорректно поставленной задачей (в частности, малые ошибки могут вызвать сколь угодно большие ошибки в производной). Для устойчивого дифференцирования функции E(x, y), заданной в виде дискретного массива данных в расчётных точках xi, yi значениями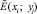 
в качестве приближения для E(x, y) примем сглаживающий кубический сплайн (СКС).
а 
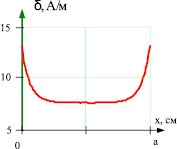б
Рис. 2. а – распределение плотности тока по объёму рельсотрона; б – профиль распределения плотности тока, где а – ширина рельсотрона
а 
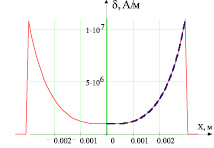б
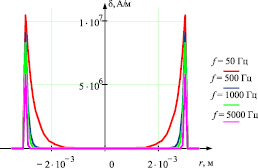
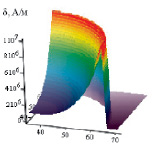
в
Рис. 3. а – распределение плотности тока по объёму проводника; б – профиль распределения плотности тока, где х – радиус проводника в метрах; в – распределение тока в цилиндрическом медном γ = 57∙106 Ом∙м проводе для разных частот
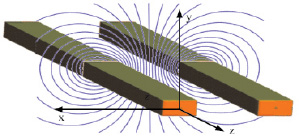
Рис. 4. Магнитное поле рельсотрона и ориентация осей декартовой системы координат для расчёта ЭМП методом конечных элементов
Вследствие того, что ток и магнитное поле распределяются внутри рельсотрона неравномерно, активное сопротивление и индуктивность для переменного тока отличаются от соответствующих значений квазистационарного тока.
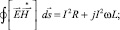
Активное и индуктивное сопротивление рельсотрона при различных частотах определим с помощью теоремы Умова – Пойтинга в комплексной форме. С этой целью рассчитаем поток Пойтинга через боковую поверхность рельсотрона на длине в 1 метр и разделим на квадрат тока, протекающего по рельсотрону; получаем комплексное сопротивление на единицу длины 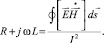[2].
(2)
Из (2) определяется индуктивность рельсотрона и активное сопротивление на единицу длины для каждой расчётной гармоники входного тока.
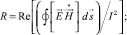
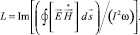
Выводы
Приводится алгоритм определения распределения тока по поперечному сечению рельсотрона при воздействии синусоидального однополярного импульса на основе разложения импульса в ряд Фурье с дальнейшим определением величин погонной индуктивности и активного сопротивления рельсотрона для каждой расчётной гармоники тока. Полученная математическая модель позволяет определить распределения тока по поперечному сечению рельсотрона с достоверной погрешностью для дальнейших исследований без использования натурного эксперимента. Апробация метода была произведена на примере расчёта плотности тока проводника круглого сечения [2, с. 168–170].
Рецензенты:
Усов Ю.П., д.т.н., профессор кафедры ЭСиЭ ЭНИН, ФГБОУ ВПО «Национальный исследовательский Томский политехнический университет», г. Томск;
Канев Ф.Ю., д.ф.-м.н., ведущий научный сотрудник, Институт оптики и атмосферы им. В.Е. Зуева СО РАН, г. Томск.
Работа поступила в редакцию 03.02.2015.