На современном этапе развития теории кинетических явлений и других свойств наноструктурированных материалов можно выделить две тенденции. С одной стороны, резко усиливается интерес к так называемым экзотическим ситуациям, мезоскопическим и размерным системам [3,4], в которых кинетическое уравнение частично или полностью неприменимо и требуется существенный квантовый подход с позиций мезонанофизики. В частности, неослабевающий интерес вызывают системы низкой размерности с различными типами локализации носителей (гетероструктуры SiC и слои), несоразмерные системы (сегнетоэлектрики), широкозонные полупроводники (А2В6, SiC, SiC-AlN) [1, 2, 5], гетероструктуры, слои, пленки для силовой электроники [5–8]. Во многих случаях описание таких систем связано с фундаментальными трудностями, вследствие чего часто отсутствует не только количественная, но даже качественная картина явлений. С другой стороны, по-прежнему актуальной остается задача количественного описания кинетических и других свойств в реальных широкозонных кристаллах, материалах и твердых растворах, в том числе на основе карбида кремния. Использование здесь преимуществ метода динамических функций Грина и компьютерного моделирования позволяет надеяться на успешное решение задачи на микроскопическом уровне.
Указанные выше два подхода в развитии современной теории кинетических и других свойств кристаллов определили содержание настоящей работы. Очевидно, что, находясь на «стыке» таких важных областей, как физика фазовых переходов и мезофизика, изучение явлений фононного и электронного переноса в реальных широкозонных кристаллах с нанокластерами, дефектами и (или) фазовыми переходами оказывается крайне востребованным.
Решение возникающих здесь вопросов требует более эффективного подхода, позволяющего учесть роль микроскопических деталей структуры, уменьшить число используемых малых параметров системы, отказаться от использования или расширить область применимости кинетического уравнения. В качестве такого подхода наиболее эффективным и универсальным является метод динамических функций Грина (МДФГ) и Кубо ‒ Гринвуда [1, 2]. В частности, МДФГ дает возможность получить точные для гармонической модели кристалла, замкнутые выражения типа Кубо ‒ Гринвуда, связывавшие коэффициенты теплопроводности и проводимости с динамическими функциями Грина системы. Тем самым вычисление неравновесных свойств кристаллов и твердых растворов сводится к задаче определения параметров системы в состоянии статистического равновесия и открывается возможность широкого использования методов функций Грина и, как следствие, количественного анализа свойств систем на микроскопическом уровне.
Ранее метод МДФГ не был приспособлен даже для случая изменения сил связи на примесном атоме. Он не был разработан и для более общих ситуаций, когда важны эффекты биений, многочастичные корреляции, флуктуации параметра порядка, гигантское усиление или подавление кинетических характеристик мезосистем. Подчеркнем, что развитие МДФГ в указанных направлениях делает его эффективным средством исследования широкого круга проблем, в том числе количественного анализа особенностей свойств в наноструктурированных широкозонных материалах и в частности на основе карбида кремния [3, 4].
1. Элементы теории линейной реакции квантовомеханической системы на внешнее возмущение (формулы Кубо)
Остановимся здесь коротко на общем квантовом подходе описания систем в термодинамике неравновесных процессов.
1.1. Двухвременные функции Грина квантовых систем. Применение формул типа Кубо ‒ Гринвуда. Как было показано выше, наиболее эффективным и наглядным способом исследования кинетических свойств широкозонных полупроводников на микроскопическом уровне в настоящее время является метод динамических двухвременных функций Грина (ФГ), компоненты Фурье которых по определению имеют вид [3, 4]
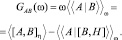 (1)
(1)
Двухвременные функции Грина (1), являясь удобным обобщением временных корреляционных функций, естественным образом возникают при рассмотрении реакции термодинамической системы на внешнее возмущение. Ввиду важности для конкретных задач формул типа Кубо ‒ Гринвуда и МДФГ остановимся кратко, но с необходимыми ссылками на соответствующую литературу на методике их получения в квантовой теории линейной реакции системы на внешнее возмущение.
1.2. Проводимость широкозонных полупроводников и мезоскопических систем. В частном случае, когда к системе приложено внешнее электрическое поле Е(t), возмущение имеет вид [1, 3]
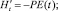
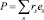 ,
,
где rs – радиус-вектор s – частицы с зарядом es. Если оператор тока I = A, то для среднего тока 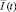 в электрическом поле E(t) получаем
в электрическом поле E(t) получаем
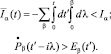 (2)
(2)
Поскольку производная от поляризации 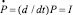 , то для проводимости системы, в частном случае стационарного возмущения, находим
, то для проводимости системы, в частном случае стационарного возмущения, находим
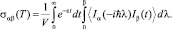 (3)
(3)
Здесь адиабатическое включение предполагает предел при ε → 0+, β = 1/kБT, kБ – постоянная Больцмана.
В частности, для широкозонных полупроводников и мезоскопических систем с относительно малой подвижностью носителей с учетом конкретного гамильтониана, для проводимости σ(Т) согласно формуле Кубо – Гринвуда (3) получаем интеграл по энергиям ε с плотностью состояний g(ε) [2,3]:
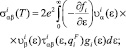 (4)
(4)
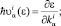
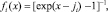 (4′)
(4′)
где 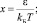
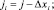
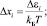
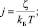
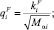 , ς и
, ς и 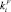 – химический потенциал и импульс Ферми, gi(ε) и Mαi – плотность состояний и эффективная масса плотности состояний в i-й долине спектра; Δεi – сдвиг дна зоны проводимости, обусловленный в данном случае спонтанной деформацией и поляризацией; kБ – коэффициент Больцмана; fi(x) – известная функция Ферми. Формулы (4) и (4′) будут использованы ниже при анализе (расчетах) особенностей поведения проводимости SiC и твердых растворов на его основе.
– химический потенциал и импульс Ферми, gi(ε) и Mαi – плотность состояний и эффективная масса плотности состояний в i-й долине спектра; Δεi – сдвиг дна зоны проводимости, обусловленный в данном случае спонтанной деформацией и поляризацией; kБ – коэффициент Больцмана; fi(x) – известная функция Ферми. Формулы (4) и (4′) будут использованы ниже при анализе (расчетах) особенностей поведения проводимости SiC и твердых растворов на его основе.
1.3. Диффузия систем с дефектами и нанокластерами. В случае наличия в системе градиента плотности или концентрации компоненты ∇zci в направлении z, диффузный поток Izi = –Di∇zc1 обусловлен возмущением [1]:
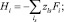
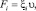
где сила Fi связана со средней скоростью υ, а коэффициент трения ξi согласно соотношению Эйнштейна связан с коэффициентом диффузии:
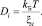
В итоге, определяя среднюю скорость переноса массы вещества, для коэффициента диффузии Di получаем
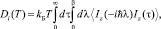 (5)
(5)
где kБ – постоянная Больцмана и 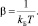
1.4. Теплопроводность систем с дефектами и нанокластерами. При термическом возмущении, обусловленном наличием отклонений от температуры ∇αT, в системе возникает поток тепла Qa за счет движущей «внешней» силы Xα = ∇αβ. Согласно теории линейной реакции для коэффициента теплопроводности kαβ = Lαβ в данном случае получаем [1‒3]
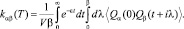 (6)
(6)
В [1, 2] показано, что для гармонического кубического кристалла с дефектами (примесями, нанокластерами) справедливо точное соотношение (обозначения см. в [1, 2]):
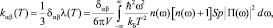 (7)
(7)
где 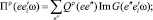
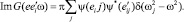 (7′)
(7′)
Формулы (7), (7′) использованы ниже при анализе поведения гигантского теплового сопротивления в А2В6 с дефектами и Ян-теллеровским фазовым переходом при TC = 14,5 °К [5, 11].
1.5. Диэлектрическая восприимчивость широкозонных полупроводников, керамики и мезоскопических систем. Однофононная функция Грина, описывая реакцию мезоскопической системы на действие внешнего зависящего от времени поля, определяет и ее динамическую восприимчивость. При этом часто можно использовать приближение, когда в массовом операторе 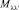 не учитывается изменение поляризации и λ = λ′. В этом случае ФГ диагональна по индексу λ и определяет динамическую восприимчивость системы χλ(q, ω) при воздействии внешнего поля с частотой ω и волновым вектором q:
не учитывается изменение поляризации и λ = λ′. В этом случае ФГ диагональна по индексу λ и определяет динамическую восприимчивость системы χλ(q, ω) при воздействии внешнего поля с частотой ω и волновым вектором q:
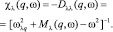 (8)
(8)
Спектральная плотность возбуждений для ветви λ и волнового вектора q связана с мнимой частью восприимчивости (ε = 1 + χ – проницаемость):
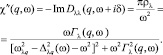 (9)
(9)
Здесь вещественная и мнимая части массового оператора
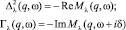 (10)
(10)
определяют перенормировку частоты и затухания возбуждений решётки соответственно.
2. Модели и расчеты кинетических явлений и характеристик широкозонных полупроводников и наноструктурированных материалов: эффекты мезоскопики
Ниже приведены результаты применения методов динамических функций Грина и формул типа Кубо ‒ Гривуда к анализу поведения и моделированию свойств ряда конкретных полупроводниковых наноструктурированных материалов.
2.1. Модели температурной и концентрационной зависимостей электрической проводимости твердых растворов и проницаемости ε(ω) керамики на основе SiC (локализация, переход Мотта, гигантское усиление ε(ω))
Учитывая (4), (4′), по аналогии с формулой для теплопроводности получаем [3]
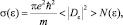 (11)
(11)
где N(e) и De – соответственно, плотность состояний и матричный элемент волнового вектора (ћk = mυ); <…> – усреднение по всем состояниям с волновыми функциями Ψl, 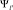 , соответствующими энергии перехода e.
, соответствующими энергии перехода e.
При достаточно низких температурах, согласно (4), (11), в системе с большим количеством примесей типа SiC может иметь место андерсоновская локализация и проводимость будет изменяться по правилу [3]:
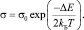 (11′)
(11′)
При еще более низких температурах может наблюдаться переход Мотта и для σ(Т) имеет место закон [3]
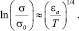 (12)
(12)
По данным экспериментов [9, 10] в работе были построены логарифмические немонотонные зависимости проводимости (ln σ) от концентрации (состава) х при различных значениях температуры (104/T) для твердых растворов карбида кремния (SiC)1-x (AlN)x и (SiC)1-x(ВеО)x.
В случае андерсоновской локализации согласно (11′) [2] на кривой 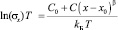 как функции состава x при х → х0 может наблюдаться точка перегиба при x = x0 (
как функции состава x при х → х0 может наблюдаться точка перегиба при x = x0 (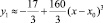 , рис. 1 (кривая 2)). При этом для показателя степени β ранее были получены разные значения (1,5; 1,8; 2,0). Если функцию ln σx(T) = y представить в виде ряда по степеням anxn, то при n = 3 и незначительных изменениях коэффициентов an
, рис. 1 (кривая 2)). При этом для показателя степени β ранее были получены разные значения (1,5; 1,8; 2,0). Если функцию ln σx(T) = y представить в виде ряда по степеням anxn, то при n = 3 и незначительных изменениях коэффициентов an 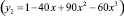 получается зависимость y(x) c минимумом слева и максимумом справа от точки x = x0 соответственно (рис. 1 (кривая 4)). Такого типа особенности в σx(T) могут наблюдаться в некоторых твердых растворах (SiC)1-x(AlN)x при x = x0. Полученные в ходе исследования данные в соответствующих областях подвергались обработке методом наименьших квадратов (рис. 1 (кривая 3)). Аналогичные зависимости также наблюдаются в твердых растворах SiC-BeO при x = x0 (рис. 2).
получается зависимость y(x) c минимумом слева и максимумом справа от точки x = x0 соответственно (рис. 1 (кривая 4)). Такого типа особенности в σx(T) могут наблюдаться в некоторых твердых растворах (SiC)1-x(AlN)x при x = x0. Полученные в ходе исследования данные в соответствующих областях подвергались обработке методом наименьших квадратов (рис. 1 (кривая 3)). Аналогичные зависимости также наблюдаются в твердых растворах SiC-BeO при x = x0 (рис. 2).
На рис. 1 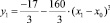 ; 3 – кривая, построенная методом наименьших квадратов по экспериментальным данным (кривая 1); 4 – кривая
; 3 – кривая, построенная методом наименьших квадратов по экспериментальным данным (кривая 1); 4 – кривая 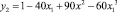 . На рис. 2
. На рис. 2 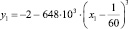 ; 3 – кривая, построенная методом наименьших квадратов по экспериментальным данным (кривая 1); 4 – кривая
; 3 – кривая, построенная методом наименьших квадратов по экспериментальным данным (кривая 1); 4 – кривая 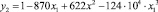 .
.
Таким образом, в работе построена модель для расчета немонотонной температурной зависимости электропроводимости в твердых растворах карбида кремния (SiC)1-x(AlN)x, (SiC)1-x(ВеО)x при различных концентрациях на основе формулы Кубо ‒Гринвуда. Построены логарифмические зависимости проводимости (ln(σ)) от концентрации х при различных значениях температуры (104/T) для твердых растворов карбида кремния (SiC)1-x (AlN)x и (SiC)1-x(ВеО)x, которые согласуются с данными соответствующих экспериментов. Рассмотрены переход Мотта и андерсоновская локализация в твердых растворах карбида кремния (SiC)1-x (AlN)x и (SiC)1-x(ВеО)x. Построены концентрационные немонотонные зависимости проводимости (SiC)1-x(AlN)x, (SiC)1-x(ВеО)x при x = x0 с использованием метода наименьших квадратов.
2.2. Гигантское тепловое сопротивление широкозонных полупроводников А2В6. В случае кубического кристалла выражение (7) несколько упрощается, а функции Грина D(ω) в случае хаотически распределенных примесей можно по методу Т-матрицы рассеяния вычислить аналитически. Тогда
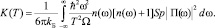 (13)
(13)
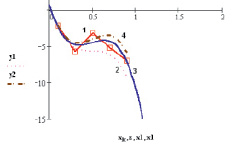
Рис. 1. Зависимость проводимости σx(T) твердых растворов (SiC)1-x(AlN)x от x: 1 – экспериментальная кривая [9, 10]; 2 – расчет
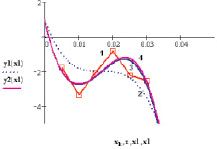
Рис. 2. Зависимость проводимости σx(T) твердых растворов SiC-BeO от x: 1 – экспериментальная кривая [9, 10]; 2 – расчет
Эта формула связывает решеточную теплопроводность K(T) с динамической функцией Грина реального кристалла Dik(ω) и справедлива для любой фиксированной конфигурации примесей, она не зависит и от конкретной микроскопической модели дефекта.
При этом в дебаевской модели кристалла с плотностью квадратов частот 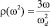 , но со временем релаксации τ(ω), учитывающим микроскопическое строение дефектов, примесей и нанокластеров, теплопроводности широкозонных полупроводников К(Т) согласно (3), (7), (7′) можно представить в виде [1–3]
, но со временем релаксации τ(ω), учитывающим микроскопическое строение дефектов, примесей и нанокластеров, теплопроводности широкозонных полупроводников К(Т) согласно (3), (7), (7′) можно представить в виде [1–3]
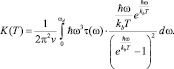 (14)
(14)
Для объяснения поведения и расчета низкотемпературной теплопроводности кристаллов ZnSе:Ni предлагается использовать как сечение резонансного рассеяния фононов на двухуровневых примесях (ионах Ni2+ с резонансной энергией между уровнями в несколько (3–5) мВ), так и сечения аномального затухания фононов около температуры структурной нестабильности ТС = 14,5 К решетки ZnSе с ионами никеля. Одновременный учет этих механизмов рассеяния фононов позволяет объяснить наблюдаемый весьма широкий (∆Т ≈ 35 К) и глубокий, K0/Kх ≈ 200 (гигантский), провал на кривой K(Т) ZnSе:Ni.
Таким образом, показано, что расчет температурной зависимости в модели Дебая при должном моделировании процессов рассеяния фононов на примесях, нанокластерах и с учетом наличия в системе фазового перехода, а также при оптимальном подборе параметров для нескольких образцов кристаллов ZnSе:Ni обеспечивает надежное согласие результатов расчета с экспериментом. Результаты расчетов для различных концентраций никеля сопоставляются с данными соответствующих экспериментов (рис. 3) по гигантскому тепловому сопротивлению в А2В6.
С использованием (14) в работе также проведены расчеты зависимости K(Т) для кристаллов ТГС и показано [5], что нетипичное поведение кривой K(Т) около Тс в кристаллах ТГС связано с крайне узким интервалом температур, в котором проявляются критические флуктуации в одноосных кристаллах (рис. 4).
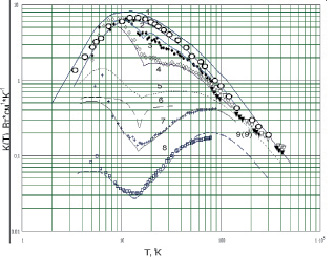
Рис. 3. Температурная зависимость теплопроводности кристаллов ZnSe. Эксперимент [11]: (сверху вниз) 1, 2 (○; ●) – «чистый» ZnSe; 3, 7, 8 – образцы ZnSe:Ni с различной концентрацией никеля: 3 (◊) – c0 = 0,00043 (1021 cm–3), 7 (+) – 0,036, 8 (▫) – 0,10
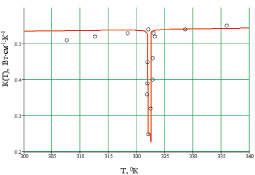
Рис. 4. Температурное поведение теплопроводности высококачественных кристаллов ТГС около Тс = 322°K в направлении [1, 12]
Таким образом, в ситуации, когда критические флуктуации (как в одноосном кристалле ТГС) относительно подавлены, а роль отдельных механизмов релаксации фононов при достаточно сильном ангармонизме (T > θ) нивелирована («осреднена»), влияние критического рассеяния фононов около Тс резко выражено. В этом случае в узкой области ΔTK, возможно, реализуется особое неравновесное (метастабильное или типа «спиновое стекло») состояние системы. При этом аномальное поведение теплопроводности вблизи Тс может оказаться весьма ярким – в крайне узком интервале температур ΔTK появляется глубокий минимум (провал: рис. 4).
2.3. Модель эффекта гигантского усиления диэлектрической проницаемости в керамике на основе карбида кремния. В случае расчета диэлектрической проницаемости в керамике при вычислении соответствующих функций Грина приходится делать ряд предположений о форме и геометрии электромагнитного осциллятора, о его поляризационных характеристиках для сферической или эллипсоидальной форм. Если допустить, что включения (нановключения) молекул и комплексов AlN в матрице SiC по своим поляризационным характеристикам обладают сфероидальной (или эллипсоидальной) формой, то за исходную теоретическую предпосылку можно взять подход Максвелла – Гарнетта [3], объясняющий усиление ε(ω) в матричных средах, содержащих включения сфероидальной (или эллипсоидальной) формы с отличающимся от единицы аспектным отношением ξ = c/a (a = b ≠ c – полуоси сфероида).
В простейшем случае выражение для ε(ω) можно получить путем замены в формуле Максвелла – Гарнетта для сферических включений фактора деполяризации сферы, равного 1/3, на фактор деполяризации сфероида 0 < Ac(ξ) < 2, отвечающего заданной ориентации поля вдоль оси с и зависящего от аспектного отношения ξ сфероида. Тогда в случае твердого раствора для ДП ε(ω) в направлении оси с получаем [5]
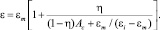 (15)
(15)
Результаты расчетов диэлектрической проницаемости сопоставляются с данными соответствующих экспериментов на рис. 5.
На рис. 5 для различных значений частоты (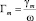 и Γi = 0) электрического поля ω: 1 – Γm = 100; 2 – 200; 3 – 420; 4 – 750; 5 – 104; Ac = 1,70;
и Γi = 0) электрического поля ω: 1 – Γm = 100; 2 – 200; 3 – 420; 4 – 750; 5 – 104; Ac = 1,70; 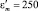 ,
, 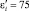 . Сплошные линии – расчет; точки – эксперимент при значениях частоты: ω = 1 МГц; 10; 0,5 и 0,1 кГц
. Сплошные линии – расчет; точки – эксперимент при значениях частоты: ω = 1 МГц; 10; 0,5 и 0,1 кГц
Обсуждение результатов и выводы
Разработанные выше модели (выражения и формулы п. 1.1–1.5)) использованы для описания свойств наноструктурированных материалов (рис. 1–5, п. 2.1–2.3). Эти свойства оказываются уникальными и определяют важную роль широкозонных полупроводников и наноструктурированных материалов в развитии элементной базы силовой электроники нового поколения [6–8]. В частности, характерные свойства SiC позволяют улучшить практически все (частотные, мощностные, прочностные) характеристики элементов (устройств) и приборов силовой электроники, оптоэлектроники и микросистемной техники. При наличии структурного фазового превращения в этих системах рассеяние фононов на частоте мягкой моды играет доминирующую роль и определяет характер аномального поведения теплового сопротивления около Тс в А2В6, ТГС и SiC. В работе построена модель переноса тепла (теплопроводности K(Т)), проведены расчеты и дана интерпретация эффекта гигантского (на два порядка – 102) увеличения теплового сопротивления в кристаллах ZnSe:Ni.
Полученные формулы (выражения) использованы для расчетов температурной зависимости теплопроводности сегнетоэлектрических кристаллов триглицинсульфата (ТГС). Показано, что аномальное поведение кривой теплопроводности К(Т) около температуры структурного фазового перехода Тс = 322°K при относительно высоких значениях температур обусловлено осреднением фононных времен релаксации (флуктуационный эффект биений). При этом критическое упругое и неупругое рассеяние фононов проявляется около Тс в виде резко выраженного узкого минимума. Результаты расчетов согласуются с данными соответствующих экспериментов.
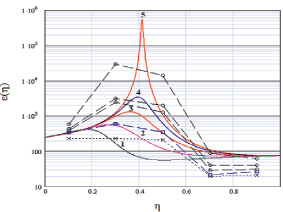
Рис. 5. Концентрационная зависимость диэлектрической проницаемости [10] керамики SiC-AlN с гигантским (на 102) усилением ε(ω) на малых частотах
Предложенные модели механизмов рассеяния фононов на дефектах, нанокластерах и около Тс [2, 5] использованы для описания особенностей температурного поведения гигантского теплового сопротивления А2В6, теплопроводности SiC и проводимости (SiC)1-x(AlN)x. Подобраны параметры времен релаксации фононов и определены последовательные стадии дефектообразования, реализующиеся по мере легирования соединений типа А2В6, кристаллов карбида кремния (SiC) и его политипов. Модель проводимости, развитая на основе формулы Кубо ‒ Гринвуда для твердых растворов (SiC)1-x(AlN)x, (SiC)1-x(ВеО)x позволила рассчитать логарифмические зависимости проводимости этих растворов (lnσх(Т)) от концентрации х (состава) при различных значениях 104/T. Выявлены особенности поведения σx(T) от состава х в твердых растворах карбида кремния:
а) обусловленные андерсоновской локализацией носителей – немонотонная зависимость σx(T) от состава х;
б) особенность, связанная с наличием перехода Мотта изолятор ‒ металл – типичные зависимости ln (σ/σ0) вида 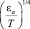 .
.
Результаты расчетов гигантского усиления диэлектрической проницаемости на низких частотах согласуются с данными экспериментов.
Таким образом, в работе продемонстрировано применение МДФГ и формул типа Кубо ‒ Гринвуда для моделирования и описания свойств (теплопроводности, проводимости, диэлектрической проницаемости и др.) широкозонных полупроводников и наноструктурированных материалов, в том числе на основе SiC. В рамках сформулированного подхода предложены модели, проведены расчеты и дана интерпретация ряда аномальных эффектов в широкозонных материалах силовой электроники. Результаты расчетов свойств и мезоскопических эффектов в широкозонных полупроводниках и наноструктурированных материалах конкретных систем позволяют надеяться, что подход МДФГ и формул типа Кубо ‒ Гринвуда применим для описания широкого спектра свойств в наноструктурированных и мезоскопических материалах.
Рецензенты:
Янукян Э.Г., д.ф.-м.н., профессор кафедры физико-математических дисциплин, декан инженерного факультета Института сервиса, туризма и дизайна (филиала) СКФУ, г. Пятигорск;
Чернобабов А.И., д.ф.-м.н., профессор кафедры физико-математических дисциплин Института сервиса, туризма и дизайна (филиала) СКФУ, г. Пятигорск.
Работа поступила в редакцию 09.02.2015.



