… одним из самых плодотворных способов описания характера изменчивости является применение соответствующего закона распределения, который определяет вероятность того, что результат измерения какого-либо параметра индивидуума, выбранного случайным образом, будет иметь любое заданное значение или лежать в определенном интервале значений …
Н. Бейли [3]
Основная информация о состоянии сердца содержится в электрокардиосигнале (ЭКС), регистрирующем прохождение электрического импульса по проводящей системе сердца. Изменение двигательной активности человека, воздействие окружающей среды и заболевания сердца влияют на форму и длительность отдельных элементов кардиоцикла. Сложность строения такого биологического объекта, как сердечно-сосудистая система, не позволяет построить однозначную математическую модель между ЭКС и состоянием отдельных анатомических органов сердца. Наличие изменчивости внутренней организации сложной структуры объекта определяет вероятностное наблюдение характерных для объекта значений. В этих случаях для описания объектов прибегают к статистическим моделям, связывающим только наиболее важные параметры объекта исследования и учитывающие наличие изменчивости его внутренней структуры.
На рис. 1 показан характерный кардиоцикл здорового человека, где отмечены положения P, Q, R, S и T зубцов. Заболевания сердца искажают отдельные элементы кардиоцикла. Вероятность перехода системы в патологическое состояние зависит от отклонений в зубцах и сегментах ЭКС. Прогнозирование поведения сложного объекта возможно на основе современных статистических методов [5].
Настоящая статья посвящена особенностям анализа ЭКС здоровых людей на основе энтропийно-параметрической обработки.
Энтропийно-параметрический подход к анализу ЭКС
Своевременное прогнозирование сердечно-сосудистых заболеваний (ССЗ) является приоритетным направлением современной медицины. В качестве эффективного инструмента выбора формы для построения математической модели объекта наблюдения следует выделить анализ энтропии результатов наблюдения, разработанный для прогнозирования АВ блокад при контроле восстановления миокарда [1]. Для получения прогноза возникновения ИМ авторами работы предложен метод контроля состояния сердечно-сосудистой системы посредством наблюдения формирования траектории для положений изображающей точки состояния системы в пространстве коэффициента энтропии и контерэксцесса результатов анализа ЭКС, полученных в течение периода наблюдения. Если траектория изображающей точки выходит за пределы области допустимых положений или наблюдается её устойчивое движение к этой границе, то контролируемой системой выдаётся автоматическое сообщение о появлении опасных симптомов развития заболевания. Ранее подобный способ исследования поведения изображающей точки сложного объекта в энтропийно-параметрических осях показал хорошие результаты при получении аппроксимаций измерений с помощью распределения Вейбулла – Гнеденко [4].
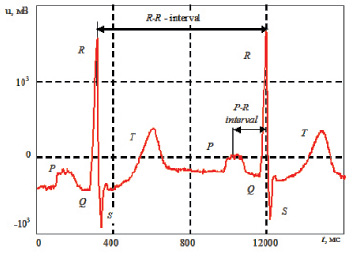
Рис. 1. Характерные интервалы кардиоцикла здорового человека
Для получения прогноза ИМ с помощью методов статистического анализа ЭКС осуществляют построение функции распределения выборки результатов в течение периода наблюдения. На рис. 2 показана характерная гистограмма распределения для одного кардиоцикла. Распределение, построенное для кардиоцикла (см. рис. 1), имеет следующие статистические параметры: коэффициент энтропии Kэ = 1,34; контрэксцесс κ = 0,286; среднее квадратическое отклонение σ = 328 мВ, коэффициент асимметрии Sk = 2,56.
Траектория изображающей точки
Непрерывный контроль состояния сердца возможен на основе наблюдения за такими характерными статистическими параметрами, как центральные моменты и энтропийно-параметрический потенциал. Наличие ССЗ обуславливает изменение формы ЭКС, что в свою очередь отразится на параметрах статистического распределения. К примеру, при исчезновении T-зубца в ЭКС, из распределения изымаются значения 3, соответствующие T-зубцу, и добавятся значения 2, близкие к изолинии (см. рис. 2).
Подобное перераспределение значений между областями группирования данных в гистограмме обусловит изменение формы распределения и уменьшение коэффициента энтропии распределения. При этом параметры распределения примут значения: коэффициент энтропии Kэ = 0,733; контерэксцесс κ = 0,21; среднее квадратическое отклонение s = 289; коэффициент асимметрии Sk = 4.
Изменение коэффициента энтропии, эксцесса и асимметрии свидетельствуют об изменении формы распределения. Следовательно, на основе контроля формы распределения значений ЭКС возможен эффективный контроль состояния пациента. Для этого ЭКС оцифровывается через временные промежутки ∆t и относительно момента времени t1 выделяется выборка результатов измерений в интервале времени [t1–Tц/2, t1 + Tц/2] одного периода кардиоцикла Tц. Тогда для расчёта центрального момента n-го порядка μn(t1) и энтропийный потенциал ∆э(t1) выборки значений в выделенном интервале для произвольного момент времени t1 справедливы выражения вида:
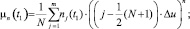(1)
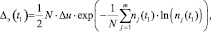(2)
где ∆u – ширина интервала группирования данных, равная отношению аппаратного заданного диапазона изменения сигнала кардиограммы uд к числу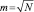 
группирования данных: 
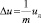; N – число значений в выборке обрабатываемого кардиоцикла: 
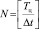; nj(t1) – число значений, попавших j-й в интервал группирования данных
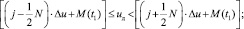
M(t1) – математическое ожидание для выборки значений за период кардиоцикла:
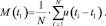(3)
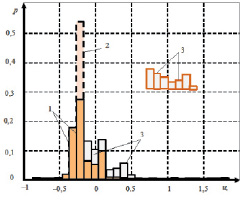
Рис. 2. Распределение выборки значений для одного кардиоцикла: 1 – распределение для кардиоцикла здорового пациента; 2 – изменение распределения при отсутствии зубца Т; 3 – распределение значений для Т-зубца
Выражения (1), (2) и (3) позволяют получить кинетические уравнения для изменения коэффициента энтропии, асимметрии и контрэксцесса во времени. Кинетическое уравнение для коэффициента энтропии получим, разделив выражение (2) для энтропийного потенциала на корень квадратный выражения (1), записанное для 2-го центрального момента:
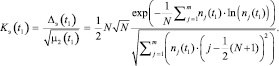(4)
Кинетическое уравнение для контрэксцеса получаем, разделив квадрат второго центрального момента μ2(t1) (выражение (1) при n = 2) на четвёртый центральный момент μ4(t1) (выражение (1) при n = 4):
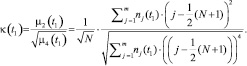(5)
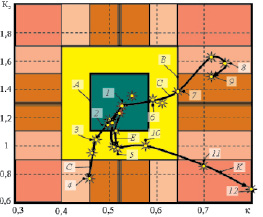
Рис. 3. Области допустимых значений для кардиограммы здорового человека в пространстве коэффициента энтропии и контрэксцесса
Если ЭКС не меняется при переходе от одного кардиоцикла к другому, то состав выборки значений также остаётся неизменным, что обуславливает неизменность центральных моментов и энтропийного потенциала. Следовательно, остаются неизменными коэффициент энтропии и контрэксцес. Наличие изменений в кардиоциклах приведёт к изменению параметров распределения. При этом изменение зубцов и сегментов ЭКС изображается в пространстве энтропийного коэффициента и контрэксцесса в виде траекторий изображающей точки. При этом различным формам ЭКС здорового пациентов в пространстве энтропийного коэффициента и контрэксцесса возможно задание такой области допустимых значений, для которой траектория изображающей точки не выйдет за пределы границ этой области.
На рис. 3 показаны области допустимых значений для кардиограммы здорового пациента в пространстве коэффициента энтропии и контрэксцесса. На данном рисунке указаны следующие обозначения: A – граница области положения изображающей точки для здоровых пациентов; B – граница области положения изображающей точки для пациентов с наличием заболевания; С – траектория перемещения изображающей точки при изменении состояния пациента от здорового в точке 1 к состоянию наличия заболевания в точке 4, диагностируемом по исчезновению T-зубца, где точки 2 и 3 соответствуют уменьшению высоты T-зубца до 60 и 40 % от исходной его высоты; D – траектория перемещения изображающей точки при изменении состояния пациента от состояния «пациент здоров» в точке 1 к состоянию ССЗ в точке 9, диагностируемому по полному исчезновению R-зубца, где точки 6, 7 и 8 соответствуют уменьшению высоты R-зубца до 70, 60 и 25 % от его начального значения; E – траектория перехода от состояния «пациент здоров» в точке 1 к состоянию ССЗ в точке 5, диагностируемому по полному или частичному исчезновению одного из зубцов: P-зубца или S-зубца; K – траектория перемещения изображающей точки от состояния «пациент здоров» в точке 1 к состоянию ССЗ «Инфаркт миокарда», диагностируемому в точках 11 и 12 по непосредственному переходу от R-зубца к T-зубцу на высоте 0,8 от высоты T-зубца и на высоте половины R-зубца соответственно. Точка 10 соответствует началу развития «инфаркта миокарда».
Заключение
Таким образом, статистический анализ выборки измерений ЭКС за один кардиоцикл может устанавливать наличие ССЗ на основании исследования статистических параметров функции распределения в пространстве энтропийного коэффициента и контрэксцесса посредством контроля результатов статисческого анализа ЭКС по положению изображающей точки. Для этого выделена область допустимых статистических параметров, при которых патологии отсутствуют. Отклонение энтропии или контрэксцесса выборки результатов ЭКС за пределы допустимой области значений свидетельствует о наличии искажения ЭКС, что в свою очередь свидетельствует о какой-либо имеющейся патологии сердца. Выделение в пространстве коэффициента энтропии и контрэксцесса областей «Здоров», «Возможно ССЗ» и «Болен» позволяет проводить предварительный диагноз ССЗ в автоматическом режиме, который способен сигнализировать о необходимости введения ограничений на двигательную активность и, при необходимости, срочном обращении за неотложной помощью в медицинское учреждение. Использование смартфона в качестве платформы для такой системы позволяет выполнять анализ ЭКС при мониторинге состояния человека в условиях свободной двигательной активности. Также следует отметить, что рассмотренный анализ патологий ЭКС выполняется по «искажению» кардиосигналов с помощью вычислительных средств без участия высококвалифицированного медицинского персонала.
Рецензенты:
Чувыкин Б.В., д.т.н., профессор кафедры «Информационно-вычислительные системы», ПГУ, г. Пенза;
Трофимов А.А., д.т.н., профессор, заместитель начальника учебно-научного центра ОАО «НИИФИ», г. Пенза.
Работа поступила в редакцию 09.02.2015.