Scientific journal

Fundamental research

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

Для описания характера движений нижней челюсти считается целесообразным применение математических методов биомеханики. За точки отсчёта принимают зубы и мыщелковые отростки нижней челюсти. В работах Я.Ф. Рутнер [3], S.C. Ferré et al. [7; 8]; P. Okeson Jeffrey [9] показано, что описание движений нижней челюсти относительно неподвижных костей черепа (суставная ямка височной кости и верхняя челюсть) можно рассматривать как поступательное перемещение и вращение вокруг трех взаимно перпендикулярных осей. Выявлено наличие наложения направлений движения нижней челюсти, формирующих результирующие моменты её перемещения в пространстве. Основные движения нижней челюсти: перемещение вниз и вверх; правая и левая латеротрузии; протрузия; ретрузия. Описание движений проводится на качественном уровне, что не позволяет точно проанализировать возникающие изменения в характере движений и возможном влиянии на это целостности зубного ряда и (или) изменения вертикально-горизонтального соотношения зубных рядов.

Для получения точного описания движений нижней челюсти применимы методы координатного определения положения твёрдого тела. В кинематике твердого тела показывается, что любое его перемещение вокруг неподвижного центра можно представить как три последовательных, отсчитываемых в определенной последовательности поворота вокруг осей координат, связанных с движущимся телом. Величины трех углов поворота будут однозначно определять ориентацию тела в пространстве. Следовательно, возникает потребность совокупного анализа результирующих моментов движения, позволяющего получать точные количественные характеристики этого процесса.

Цель исследования – разработать способ координатного определения положения нижней челюсти человека при различных функциональных позициях.

Материал и методы исследования

Использованы методы кинематического описания движения твёрдого тела, применяемые в классической механике.

Результаты исследования и их обсуждение

Характер движения нижней челюсти определяют критерии артикуляционной нормы [5]. В классической механике взаимное положение двух тел принято задавать при помощи двух декартовых систем координат, каждая из которых неизменно связана со своим телом [2; 6]. Для определения положения нижней челюсти относительно черепа введем в рассмотрение две декартовы системы координат, одна из которых – Оxyz – неподвижна относительно черепа, а вторая – Аξης ‒ неизменно связана с нижней челюстью. Будем считать, что в случае, когда челюсти сомкнуты, эти системы координат совпадают друг с другом и их оси параллельны линиям пересечения сагиттальной, окклюзионной и туберальной плоскостей. Ось Ох направлена вперед параллельно линии пересечения сагиттальной и окклюзионной плоскостей, ось Oz располагается в сагиттальной плоскости и направлена перпендикулярно оси Ох вверх, а ось Оу направлена влево параллельно линии пересечения туберальной и окклюзионной плоскостей. Начало систем координат совместим с серединой отрезка, соединяющего самые дистальные точки головок нижней челюсти в центральной окклюзии (рис. 1).

Перемещение нижней челюсти можно рассматривать как сумму поступательного перемещения вместе с точкой А и поворота вокруг этой точки. Первая часть перемещения полностью описывается изменением координат хА, уА, zА точки А в неподвижной системе координат. Для определения взаимной угловой ориентации двух систем координат применим расчёт при помощи угловых координат, т.к. максимальные значения углов поворота сравнительно невелики (не больше π/4 или 45°). Но в любой системе угловых координат существуют такие критические значения отдельных координат, при которых оси двух других поворотов сливаются и соответствующие им координаты нельзя различить.

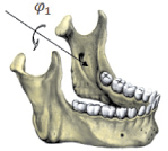
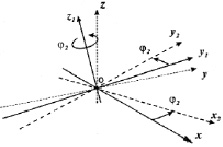
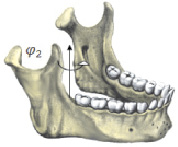
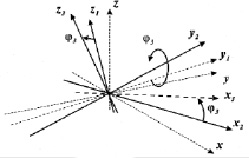
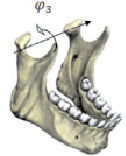
Так как при движении нижней челюсти подвижная и неподвижная системы координат лишь незначительно перемещаются и отклоняются друг относительно друга, следует использовать углы, которые называются углами Брайнта или углами Кардана [2; 6]. Используя данные S.C. Ferré, R. Logoux, J.L. Helary et all [8], отсчёт этих углов производим последовательно. Первый из этих углов – φ1 – есть угол поворота подвижной системы координат вокруг исходного положения оси Оξ, совпадающей с неподвижной осью Ох (рис. 2, а). После него оси подвижной системы координат займут промежуточное положение Оу1 и Oz1. Второй – φ2 есть угол поворота подвижной системы координат вокруг нового положения оси Оς или Oz1 (рис. 2, б). При этом оси Оξ и Оη займут новое положение Ох2 и Оу2. Он соответствует трансверзальным движениям нижней челюсти. И, наконец, поворот на третий угол φ3 вокруг промежуточного положения оси Оη или Оу2 переводит оси подвижной системы координат в конечное положение (рис. 2, в). Этот поворот в основном определяет сагиттальные движения.

Выбор подобной системы угловых координат определяется следующими обстоятельствами:

1. Нижняя челюсть является подвижным элементом системы артикуляции. Систему артикуляции образуют: кости лицевого отдела черепа, ВНЧС, мускулатура, определяющая движения нижней челюсти, подъязычная кость и зубные ряды, в одном из типов физиологического прикуса [5]. Нарушение взаимосвязей между элементами системы артикуляции приводит к смене «привычного» типа жевания, фонетики и, соответственно, окклюзии зубных рядов, что сказывается на характере распределения механических напряжений в костно-мышечном комплексе челюстно-лицевой области.

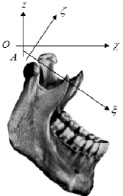
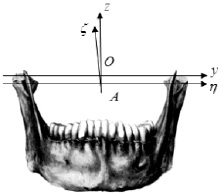
Рис. 1. Взаимное расположение подвижной Аξης, и неподвижной Оxyz систем координат при отведении нижней челюсти в положение рот открыт

2. Данный набор углов позволяет однозначно определить взаимную угловую ориентацию при небольших значениях углов. При таком порядке поворотов вокруг осей существует критический случай при φ2 = π/2, что выходит за пределы возможных значений рассматриваемых углов.

3. При малых значениях углов повороты вокруг осей можно рассматривать как независимые, и с достаточной степенью точности можно считать, что повороты происходят вокруг исходных положений осей. То есть угол φ1 определяет величину поворота нижней челюсти в туберальной плоскости, угол φ2 – величину поворота при трансверзальных движениях и, наконец, угол φ3 – величину поворота при сагиттальных движениях.

4. Абсолютные величины максимальных значений углов удовлетворяют следующему условию φ1 < φ2 < φ3.

При движении челюсти одновременно изменяются все угловые координаты. Соотношение между ними определяется многими факторами: целевой функцией осуществляемого движения, состоянием зубов и суставов, видом пищи и т.д.

Итак, положение нижней челюсти относительно верхней можно определить шестью координатами:

хА = хА(t)φ1 = φ1(t);

уА = уА(t)φ2 = φ2(t);

z1 = z1(t)φ2 = φ2(t).

Назовем их, как принято в классической механике, обобщенными координатами. Выбирая различные виды функциональной зависимости обобщенных координат от времени (или условного времени), можно получить аналитические уравнения, определяющие характер движения челюсти. В механике такие уравнения называются законом движения.

Если известны эти уравнения, т.е. закон движения нижней челюсти относительно верхней, то с их помощью по формулам преобразования координат [2] определим координаты, задающие положение любых точек нижней челюсти относительно верхней. Если для некоторой точки известны координаты ξ, η и ς в подвижной системе координат, т.е. расположение ее на нижней челюсти, то положение этой точки относительно верхней челюсти будет определяться координатами х, у и z по следующим формулам:

х = хА + ξ∙cos a11 + η∙cos а12 + ς∙cos а13;

у = уА + ξ∙cos a21 + η∙cos а22 + ς∙cos а23; (*)

z = zА + ξ∙cos a31 + η∙cos а32 + ς∙cos а33.

В этих формулах ξ, η и ς – координаты наблюдаемой точки в подвижной системе координат (на челюсти), cos а – направляющие косинусы, матрица которых для выбранных угловых координат имеет следующий вид:

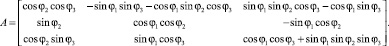
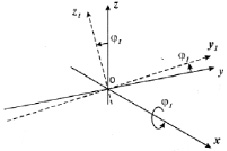
а

б

в

Рис. 2. Последовательность поворотов при определении угловой ориентации: а – угол вращения нижней челюсти вокруг сагиттальной оси в положении физиологического покоя; б – угол вращения нижней челюсти вокруг вертикальной оси в пределах окклюзионной плоскости; в – угол вращения нижней челюсти вокруг фронтальной (трансверзальной) оси

Если величины углов поворота не превышают нескольких угловых градусов или поворот происходит в основном вокруг только одной оси, для пересчёта координат можно использовать более простые соотношения:

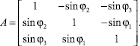
Если при исследовании потребуется найти, какое положение займет челюсть, под действием приложенных к ней мышечных усилий, то понадобятся геометрические уравнения, аналитически описывающие взаимодействующие суставные поверхности височно-нижнечелюстного сустава.

При различных исследованиях характер движения нижней челюсти обычно определяется по траектории движения и координатам некоторых характерных точек, расположенных на челюсти или отдельных зубах. Эти траектории чаще всего изображают в сагиттальной или туберальной плоскостях. Для сравнения графического и аналитического способа описания движения нижней челюсти используем экспериментальные траектории движения пяти различных точек челюсти, расположенных симметрично относительно ее оси, как показано ранее [9]. Схема расположения опорных точек приведена на рис. 3.

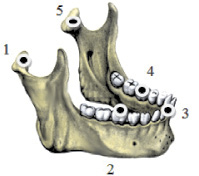
Рис. 3. Расположение контрольных точек на нижней челюсти

Были определены координаты опорных точек для каждого из восьми зафиксированных, согласно известным положениям [9]. Затем для этих координат составлялись уравнения (*) и решались относительно неизвестных координат. Получить аналитическое решение системы из шести нелинейных алгебраических уравнений (1) невозможно, поэтому ее решение проводилось численным методом с использованием математического пакета Maple VI. В результате были получены законы изменения координат в процессе жевания. Эти результаты представлены в таблице.

Полученные графики, рассчитанные по траекториям приведенного в [9] движения, показывают, что в процессе жевания наибольшей величины достигает угол φ3, который характеризует открытие челюсти. Его изменение происходит почти по гармоническому закону. Поворот на угол φ2, который в первом приближении описывает поворот челюсти в горизонтальной плоскости, начинается почти с начала фазы закрытия челюсти и происходит только в одном направлении – в направлении нерабочей стороны. Изменение угла φ1 начинается также при закрытии челюсти, но носит переменный характер, что, вероятно, можно объяснить скольжением друг по другу окклюзионных контактов зубов-антагонистов верхней и нижней челюстей.

Изменение значений линейных и угловых координат в процессе жевания

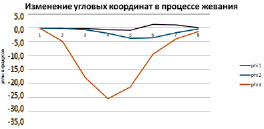
Рис. 4. График изменения угловых координат в процессе жевания от координат точек нижней челюсти

Выводы

Использование выбранных координат позволяет составить общие уравнения равновесия сил взаимодействия органов зубочелюстной системы, исследовать зависимости этих сил от положения нижней челюсти. Рассмотренный способ аналитического описания движения нижней челюсти позволяет получать точные количественные характеристики как происходящих при жевании движений, так и тех отклонений от нормы, которые наблюдаются у конкретного пациента. Мы получили кинематическую модель движения нижней челюсти в виде шести нелинейных алгебраических уравнений, описывающих траекторию движения нижней челюсти в обобщенных координатах движения вокруг сагиттальной, вертикальной и трансверзальной осей. Разработанная модель позволяет рассчитать нагрузку на основные элементы нижней челюсти в заданных оператором точках, прогнозировать нормальный или патологический процесс развития нижней челюсти и системы артикуляции в целом. При накоплении соответствующего базового материала эти количественные характеристики могут быть использованы при диагностике состояния суставных поверхностей.

Потапов В.П., д.м.н., профессор, декан стоматологического факультета, ГБОУ ВПО «Самарский государственный медицинский университет» Минздрава России, г. Самара;

Хаймович И.Н., д.т.н., профессор кафедры «Информационные системы и компьютерные технологии», ЧОУ ВО «Международный институт рынка», г. Самара.

Работа поступила в редакцию 06.03.2015.