В статье рассматривается влияние критичных конструктивных параметров прецизионного вибрационного датчика ускорения на частоту колебаний, а именно радиуса закругления упругого элемента и коэффициента вязкости материала, что позволяет определить управляющие параметры технологического процесса (параметры режима термообработки), обеспечивающие необходимый размер зерна и коэффициент вязкости материала. Полученные зависимости являются основой для разработки информационной системы, позволяющей оценивать степень влияния следующих конструктивных параметров: радиуса закругления и внутреннего трения материала, – на функциональные характеристики вибрационного датчика
Цель исследования – проанализировать способы обеспечения стабильности функциональных характеристик датчика с учетом параметров процесса и эксплуатации, в частности при изменении температуры. Сформулировать основные положения разработки информационной системы для оценки влияния следующих конструктивных параметров: радиуса закругления и внутреннего трения материала – на функциональные характеристики вибрационного датчика.
Одним из основных модулей информационной системы является модуль, содержащий экспериментальные зависимости между параметрами технологического процесса и конструктивными параметрами.
Материал и методы исследования
Произведен анализ частот свободных колебаний стержня в среде без сопротивления при различных типах граничных условий. Произведен анализ влияния внутреннего трения на частоту свободных колебаний чувствительного элемента.
Результаты исследования и их обсуждение
Решены новые задачи по оценке влияния критичных конструктивных параметров на выходные характеристики датчика. Показано, в частности, что режимы термообработки оказывают существенное влияние на частоту колебаний и функциональные характеристики датчика.
Практическое использование
Возможность выбора параметров технологического процесса изготовления, в том числе режимов термообработки, обеспечивающих критичные конструктивные параметры и функциональные характеристики.
Разработанная информационная система, учитывающая материал деталей, свойства внешних воздействий, конструктивные и технологические параметры, позволила разработать способы управления технологическим процессом, позволяющие получить требуемые выходные параметры. Информационная система планируется для использования при анализе отклонения параметров технологического процесса от номинального значения при реальных условиях работы. Применение информационной системы позволяет повысить эффективность процесса сборки и настройки с использованием модулей конструктивных решений, аналитических и экспериментальных зависимостей.
Полученные аналитические и экспериментальные зависимости использованы при разработке новых конструкций вибрационных датчиков с существенно большей частотой колебаний и являются основой информационной системы для данной разработки.
Схема вибрационного датчика показана на рис. 1.
На рис. 1 показаны: 1 – корпус прибора, 2 – чувствительный элемент с инерционным телом, 3 – упругая перемычка.
В приборе чувствительный элемент совершает поперечные колебания, которые создаются электромагнитным возбудителем. При действии на прибор линейного ускорения на чувствительный элемент действует растягивающая или сжимающая продольная сила, изменяющая частоту упругих колебаний. Знание зависимости частоты колебаний от ускорения позволяет определить истинное значение ускорения.
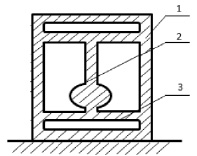
Рис. 1. Схема вибрационного датчика
Чувствительный элемент представляет собой однородный стержень (балку) прямоугольного сечения с различными условиями закрепления концов. На первом этапе определены собственные частоты колебаний в среде без сопротивления (без учета внутреннего трения). С использованием методов математической физики составлено дифференциальное уравнение свободных колебаний – уравнение в частных производных [1, 2]. Общее решение уравнения выражено через гиперболические и тригонометрические функции. Для определения произвольных постоянных приведены граничные условия на концах стержня при закреплении концов различным способом. Для различных типов граничных условий получены частоты собственных колебаний.
Алгоритм анализа частот свободных колебаний стержня в среде без сопротивления при различных типах граничных условий может быть представлен следующей схемой (рис. 2).
Выполненные с учетом предложенного алгоритма расчеты позволили установить, что ширина чувствительного элемента не является критичным параметром, а его длина, получаемая с учетом технологических радиусов закругления, определенным образом влияет на частоту. Радиус закругления изменяет также характер закрепления чувствительного элемента (граничные условия), что показано на рис. 3.
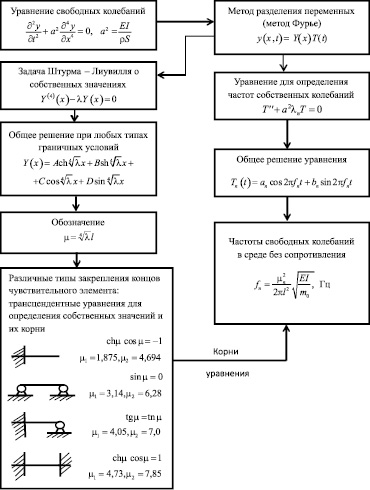
Рис. 2. Схема анализа частот свободных колебаний
При учете влияния внутреннего трения материала на свободные колебания чувствительного элемента принято, что основной причиной внутреннего трения являются пластические деформации частиц (зерен, волокон) тела, обусловленные неоднородностью его микроструктуры. Для учета внутреннего трения принята гипотеза Фохта [3, 4], а связи напряжений с деформацией и скоростью деформации:
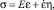
где Е – модуль упругости, Н/м2; η – коэффициент вязкости материала, (Н∙с)/м2.
Алгоритм учета влияния внутреннего трения на частоту свободных колебаний чувствительного элемента можно представить в виде следующей схемы (рис. 4).
Влияние режимов термообработки на размер зерна для используемого материала (сплав 45НХТ) приведено в работах [5, 6]. Требуемый размер зерна 20…50 мкм может быть получен при закалке с температурой Т = 890 °С и выдержкой в течение 15 мин (или при закалке с температурой Т = 950 °С и выдержкой в течение t = 10 мин). Дальнейшее увеличение времени выдержки приводит к увеличению размеров зерна до 150 мкм. Размер зерна оказывает непосредственное влияние на характеристику внутреннего трения – коэффициент вязкости материала. При изменении размера зерна от 20 до 50 мкм коэффициент вязкости изменяется примерно от 60 до 20 (Н∙с)/м2, что установлено путем обработки экспериментальных данных (рис. 5).
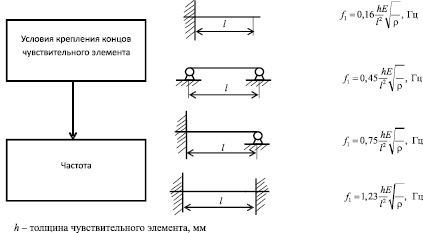 Рис. 3. Влияние условий крепления чувствительного элемента на частоту
Рис. 3. Влияние условий крепления чувствительного элемента на частоту
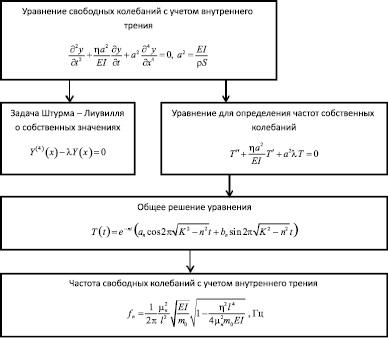
Рис. 4. Схема учета влияния внутреннего трения на частоту свободных колебаний
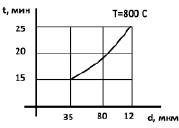
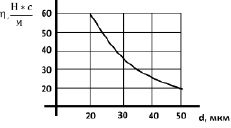
а б
Рис. 5. Влияние режимов термообработки и размеров зерна на коэффициент вязкости: а – зависимость размера зерна от времени выдержки; б – зависимость коэффициента вязкости от температуры
Аналитические зависимости для частоты собственных колебаний с учетом внутреннего трения позволяют оценить влияние режимов термообработки на функциональные характеристики прибора – частоту чувствительного элемента, разностную частоту вибрационного датчика.
Представленные в статье алгоритмы являются основой для разработки информационной системы, позволяющей оценивать степень влияния следующих конструктивных параметров: радиуса закругления и внутреннего трения материала, – на функциональные характеристики вибрационного датчика.
Заключение
Практически впервые установлена связь частоты собственных колебаний с металловедческими аспектами – режимами термической обработки. Выполнены аналогичные исследования по оценке влияния режимов механической обработки (в частности, скорости резания) на толщину дефектного слоя, эффективный модуль упругости материала и в конечном счете, на частоту собственных колебаний. Полученные аналитические и эксперементальные зависимости использованы при разработке новых конструкций вибрационных датчиков с существенно большей частотой колебаний. Информационная система, позволяющая оценивать степень влияния следующих конструктивных параметров: радиуса закругления упругого элемента и внутреннего трения материала на функциональные характеристики вибрационного датчика, ‒ позволяет уменьшить количество несоответствий при производстве.
Рецензенты:Чечулин Ю.Б., д.т.н., профессор кафедры «Детали машин» Механико-машиностроительного института, Уральский федеральный университет имени первого Президента России Б.Н. Ельцина, г. Екатеринбург;
Паршин В.С., д.т.н., профессор, заведующий кафедрой «Металлургические и роторные машины» Механико-машиностроительного института, Уральский федеральный университет имени первого Президента России Б.Н. Ельцина, г. Екатеринбург.
Работа поступила в редакцию 06.03.2015.



