Тензор проводимости многодолинного полупроводника с учетом деформации решетки и структурного фазового перехода. Отметим, что даже в случае такого типичного полупроводника, каким является GeТе, до сих пор нет последовательной количественной теории проводимости, а вопрос о причине ее аномального поведения около Тc остается дискуссионным [5–6]. В общем случае проводимость σαβ(Т) полупроводника типа GeTe определяется суммой вкладов σiαβ отдельных долин i = 1, 2, 3, 4, расположенных [2] соответственно на осях [III], [IIĪ], [IĪI] и [ĪII]. Тензор проводимости i-й долины в предположении изотропной связи между кинетической энергией носителей ε и приведенным квазиимпульсом qi имеет вид [3–4]
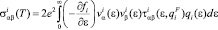 , (1)
, (1)
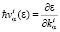 ,
, 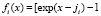 , (2)
, (2)
где 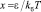 ,
, 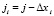 ,
, 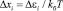 ,
, 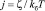 ,
, 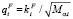 , ζ и
, ζ и 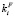 – химический потенциал и импульс Ферми, q(e) и Mαi – плотность состояний и эффективная масса плотности состояний, Dei – сдвиг дна зоны проводимости, обусловленный в данном случае спонтанной деформацией и поляризацией. Спектр носителей находится путем диагонализации основной части исходного гамильтониана [9, 13]. Перенормированные вершины динамического межзонного
– химический потенциал и импульс Ферми, q(e) и Mαi – плотность состояний и эффективная масса плотности состояний, Dei – сдвиг дна зоны проводимости, обусловленный в данном случае спонтанной деформацией и поляризацией. Спектр носителей находится путем диагонализации основной части исходного гамильтониана [9, 13]. Перенормированные вершины динамического межзонного 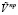 и внутризонного
и внутризонного 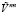 электрон-фононного взаимодействия, определяющие скорость релаксации носителей в случае квазиупругого рассеяния (
электрон-фононного взаимодействия, определяющие скорость релаксации носителей в случае квазиупругого рассеяния (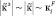 – импульс Ферми), не зависят от малого переданного импульса
– импульс Ферми), не зависят от малого переданного импульса 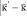 . Диагональное в главных осях i-го экстремума обратное время релаксации носителей можно при этом представить в виде
. Диагональное в главных осях i-го экстремума обратное время релаксации носителей можно при этом представить в виде
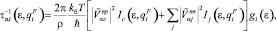 (3)
(3)
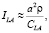
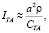
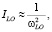
где j = LA, TA, LO, CLA и СLA – аномально зависящие от температуры эффективные упругие постоянные LA и TA фононов, r – плотность, a – постоянная решетки. Интеграл столкновений IC, обусловленный рассеянием носителей на мягкой моде (ТО-фононах), имеет вид [13]
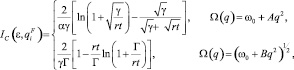 (4)
(4)
где 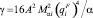 – параметр интеграла столкновений Ic;
– параметр интеграла столкновений Ic; 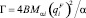 ,
, 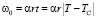 в приближении среднего поля r = 2 при Т < Тc, r = 1 при Т > Тc.
в приближении среднего поля r = 2 при Т < Тc, r = 1 при Т > Тc.
Анизотропия проводимости в отдельной долине целиком определяется временем релаксации ταi и массами носителей 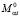 , тогда как анизотропия полной проводимости при заданных ταi и
, тогда как анизотропия полной проводимости при заданных ταi и 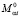 существенно связана со сдвигом (по энергии)
существенно связана со сдвигом (по энергии) 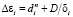 экстремумов спектра, обусловленными спонтанной деформацией и поляризацией.
экстремумов спектра, обусловленными спонтанной деформацией и поляризацией.
Анизотропия электрического сопротивления и аномальная температурная зависимость σαβ(Т) около Тс. В ромбоэдрической (α) фазе 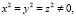
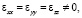
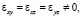
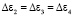 и в системе с осью z, направленной по [III], компоненты полной проводимости
и в системе с осью z, направленной по [III], компоненты полной проводимости
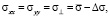 (5)
(5)
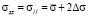
определяются значениями
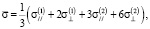 (6)
(6)
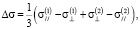
причем
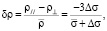
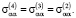 (7)
(7)
В ромбической (g) фазе x2 = y2 ≠ 0, z2 = 0, 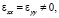
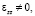
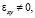
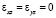 согласно
согласно 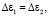
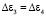
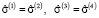 (8)
(8)
и в системе осей 1–[100], 2–[110], 3–[001] получаем:
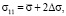
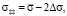
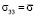 , (9)
, (9)
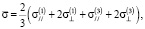 (10)
(10)
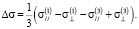 (11)
(11)
Интегралы столкновений Ic и Ij в (3–4) слабо зависят от 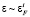 , а также от номера долины i. В итоге выражение для проводимости можно свести к двухпараметрическому интегралу Ферми [3]. Тогда с учетом (1)–(11), например, для анизотропии и продольной компоненты сопротивления
, а также от номера долины i. В итоге выражение для проводимости можно свести к двухпараметрическому интегралу Ферми [3]. Тогда с учетом (1)–(11), например, для анизотропии и продольной компоненты сопротивления 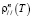 в ромбоэдрической фазе, получаем
в ромбоэдрической фазе, получаем
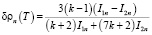 , (12)
, (12)
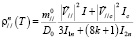 , (13)
, (13)
где
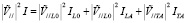 ,
,
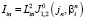 ,
,
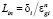 ,
, 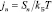 ,
, 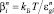 ,
,
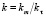 ,
, 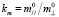 ,
,
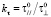 ,
, 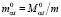 ,
,
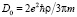 ,
, 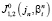 .
.
Это обобщенный интеграл Ферми, m – масса свободного электрона.
Анизотропия сопротивления dr3 в ромбической фазе, в частности, относительно оси 3–[001] составляет
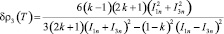 . (14)
. (14)
В случае сильно вырожденного полупроводника (например, SnTe) полученные выше формулы существенно упрощаются:
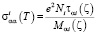 , (15)
, (15)
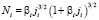 ,
, 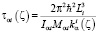 , (16)
, (16)
где
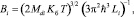
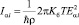 , (17)
, (17)
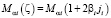 ,
, 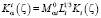 ,
, 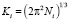 ,
, 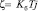 .
.
При условии полного вырождения (z ≥ 5),например, для a-фазы имеем z = 1, N1 = N и при 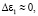
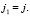
Ниже при определении параметров теории будут также использоваться данные о подвижности носителей 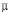 в поликристаллических образцах, поэтому приведем соответствующее выражение для
в поликристаллических образцах, поэтому приведем соответствующее выражение для 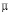 . В предположении слабого рассеяния носителей на границах отдельных монокристаллов [7] для a- и b-фаз получаем:
. В предположении слабого рассеяния носителей на границах отдельных монокристаллов [7] для a- и b-фаз получаем:
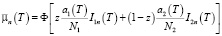 , (18)
, (18)
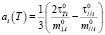 ,
,
где z – доля носителей, находящихся в первой долине 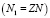 ,
, 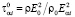 – приведенное время релаксации:
– приведенное время релаксации:
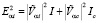 ,
,
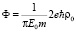 , (19)
, (19)
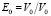 (V0 = 1 эВ, r0 = I г/см3, v0 = 105 см/сек, N0 = 1020 см–3, а индекс n = N/N0 в (12)–(18) отражает зависимость r// и dr от концентрации носителей N.
(V0 = 1 эВ, r0 = I г/см3, v0 = 105 см/сек, N0 = 1020 см–3, а индекс n = N/N0 в (12)–(18) отражает зависимость r// и dr от концентрации носителей N.
Численный анализ параметров теории и анизотропии электрической проводимости. Исходя из имеющихся в наличии данных по GeTe и SnТе в работе была предложена последовательная схема определения параметров теории.
Эффективная масса плотности состояний. В случае 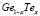 с учетом данных [7], получены значения эффективной массы
с учетом данных [7], получены значения эффективной массы 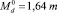 и приведенного химического потенциала zn(T) для различных N. Эти данные использовались для расчета зависимости подвижности
и приведенного химического потенциала zn(T) для различных N. Эти данные использовались для расчета зависимости подвижности 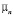 и проводимости
и проводимости 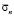 от концентрации носителей N при Т = 100 и 800 К (рис. 1). Перераспределение носителей между долинами спектра ведет к аномальной при Т << ТC зависимости подвижности
от концентрации носителей N при Т = 100 и 800 К (рис. 1). Перераспределение носителей между долинами спектра ведет к аномальной при Т << ТC зависимости подвижности 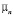 от концентрации носителей (кривая 2 на рис. 1) и к появлению при T < TC анизотропии проводимости.
от концентрации носителей (кривая 2 на рис. 1) и к появлению при T < TC анизотропии проводимости.

Рис. 1. Рассчитанная зависимость подвижности (1, 2) и
проводимости (3, 4) поликристаллов GeТе от концентрации носителей при
800 К – (1,3) и 100 К – (2,4), точки ( ) и квадратики (
) и квадратики ( )экспериментальные данные [7]
)экспериментальные данные [7]
Анизотропия сопротивления. По формуле для dr и данным [7, 10, 12] при N = 8,5.1020см–3 для GeTe определен коэффициент анизотропии K(T) и рассчитана зависимость dr от N. Оказалось, что в интервале 300–600 К анизотропия drn заметно увеличивается с уменьшением концентрации носителей. Для Т << Тc dn ≈ 3(K – 1)/(K – 2), 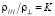 и с учетом данных [7, 10, 12] имеем K ≈ 2.
и с учетом данных [7, 10, 12] имеем K ≈ 2.
Аномальная зависимость сопротивления от температуры. Численный анализ показывает, что поведение сопротивления dr//(T) вблизи Тc существенно зависит от эффективной скорости релаксации носителей на ТО-фононах.
При скоростях релаксации 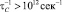 зависимость r(T) вблизи Tc имеет вид излома или даже характер логарифмической особенности, как в SnТе [1, 8, 13]. При
зависимость r(T) вблизи Tc имеет вид излома или даже характер логарифмической особенности, как в SnТе [1, 8, 13]. При 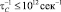 и относительно больших D0(T) (~ 0,3 эВ при Т → 0) аномалия сопротивления около Тc имеет вид плавного несимметричного максимума (GеТе). Рассчитанная для GеТе зависимость r//(T) при γ = 300 К хорошо согласуется с экспериментом (рис. 2). При расчете сопротивления GeTe и SnTe соответственно использовались данные Тc = 665 и 97,5 К; r = 6,19 и 6,45 г/см3, а = 6,01 и 6,33 A.
и относительно больших D0(T) (~ 0,3 эВ при Т → 0) аномалия сопротивления около Тc имеет вид плавного несимметричного максимума (GеТе). Рассчитанная для GеТе зависимость r//(T) при γ = 300 К хорошо согласуется с экспериментом (рис. 2). При расчете сопротивления GeTe и SnTe соответственно использовались данные Тc = 665 и 97,5 К; r = 6,19 и 6,45 г/см3, а = 6,01 и 6,33 A.
Характер аномалии r(T) около Тc существенно зависит от g (рис. 2) и тем самым, согласно (2), от параметров и вида дисперсии мягкой моды.

Рис. 2. Температурная зависимость электросопротивления монокристалла α – GeTe: а) точки и крестики – экспериментальные значения  – 1(2) 3; б) штрихпунктирная линия – рассчитанное
– 1(2) 3; б) штрихпунктирная линия – рассчитанное  – 1(2), представляющее собой суммy остаточного, нормального
– 1(2), представляющее собой суммy остаточного, нормального  и аномальных
и аномальных  и
и  сопротивлений; сплошная линия –
сопротивлений; сплошная линия –  – 1(2) с учетом аномального
– 1(2) с учетом аномального  сопротивления при γ = 300; пунктир и точки – ρ// при γ = 200 и 100 (γ – параметр интеграла cтолкновений IC)
сопротивления при γ = 300; пунктир и точки – ρ// при γ = 200 и 100 (γ – параметр интеграла cтолкновений IC)
Выводы
Таким образом, показано, что в зависимости от величины эффективной скорости релаксации носителей на мягких ТО-фононах (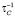 ) и междолинного расщепления D0(T) аномалия проводимости вблизи Тc в соединениях A4B6 может иметь вид излома или вид плавного несимметричного максимума. Рассчитаны аномальная зависимость подвижности от концентрации носителей и анизотропия проводимости в a- и b-фазах GеТе. В итоге:
) и междолинного расщепления D0(T) аномалия проводимости вблизи Тc в соединениях A4B6 может иметь вид излома или вид плавного несимметричного максимума. Рассчитаны аномальная зависимость подвижности от концентрации носителей и анизотропия проводимости в a- и b-фазах GеТе. В итоге:
1. Рассчитана проводимость сегнетоэлектриков-полупроводников GeTe и SnTe с использованием их реальных многодолинных электронных спектров. Учитывается рассеяние носителей на LA, ТА и мягких ТО-фононах.
2. Показано, что аномальное вблизи Тc сопротивление может иметь вид излома (SnТе) или плавного несимметричного максимума (GеТe).
3. Рассчитаны обусловленные междолинным расщеплением спектра, анизотропия сопротивления и аномальная зависимость подвижности от концентрации носителей.
4. Предложена и для GeTe реализована схема последовательного определения параметров теории.
Рецензенты:Янукян Э.Г., д.ф.-м.н., профессор, профессор кафедры физико-математических дисциплин, декан инженерного факультета филиала СКФУ, г. Пятигорск;
Чернобабов А.И., д.ф.-м.н., профессор, пофессор кафедры физико-математических дисциплин Института сервиса, туризма и дизайна филиала СКФУ, г. Пятигорск.
Работа поступила в редакцию 19.02.2015.



