В диссертационной работе автора было проведено численное и экспериментальное исследование несущей способности соединения SHERPA при изгибе в деревянных конструкциях из комбинации стеновой панели-СLT с балкой из CLT и LVL. Автором был предложен численный алгоритм для определения несущей способности соединения SHERPA при изгибе без учёта воздействия эксцентриситета, но при конструировании соединения в большепролетных конструкциях эксцентриситет значительно влияет на несущую способность соединения при изгибе. В соответствии с требованием более просторного внутреннего пространства, например, в торговом центре, на спортивном стадионе, в промышленном здании и т.д, большепролетная деревянная конструкция используется в виде дощатоклееных балок пролётом 6–24 м, дощатоклееных арок с пролётом более 100 м и деревянных рам с пролётом до 18–30 м [1]. В большепролетной конструкции крепеж SHERPA находится не только под действием нагрузки вдоль направления вставки, но и изгиба. Таким образом, при конструировании несущей способности соединения SHERPA при изгибе должен рассматриваться коэффициент эксцентриситета. Сегодня в научном исследовании компании SHERPA с Timberland (лаборатория по испытанию деревянных конструкций Технического университета г. Грац в Австрии) осуществляется несущая способность крепежа SHERPA при изгибе для достижения 280 кН [2]. При этом крепеж SHERPA может применяться в более широкой области и обеспечивать более устойчивость и безопасность.
Целью настоящей работы является сформирование численного алгоритма для определения коэффициента эксцентриситета соединения SHERPA при изгибе.
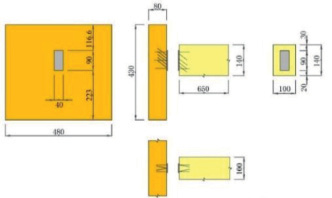
Расчётная схема по определению коэффициента эксцентриситета представлена на рис. 1.
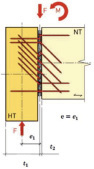
а) б) в)
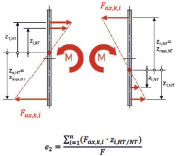
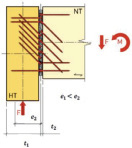
Рис. 1. Расчётная схема по определению коэффициента эксцентриситета [4]: а – предельный эксцентриситет; б – эксцентриситет металлических накладок; в – эксцентриситет изгиба
Из рис. 1 видно, что коэффициент эксцентриситета зависит от следующих факторов:
• предельного эксцентриситета в зависимости от толщины стеновой панели-CLT и металлических накладок SHERPA (рис. 1, а);
• эксцентриситета соединения SHERPA в зависимости от расположения шурупов, центра тяжести алюминиевой детали и несущей способности шурупа на выдёргивание (рис. 1, б);
• эксцентриситета изгиба в зависимости от жёсткости соединения SHERPA и прогиба балки (рис. 1, в);
Автором предложен численный алгоритм для определения несущей способности соединения SHERPA при изгибе с учётом коэффициента эксцентриситета, показанный в следующих уравнениях:
• несущая способность соединения SHERPA при изгибе F’ с учётом коэффициента эксцентриситета в соответствии с рекомендацией [4], Н:
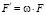 ; (1)
; (1)
 ; (2)
; (2)
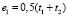 ; (3)
; (3)
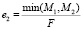 ; (4)
; (4)
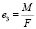 ; (5)
; (5)
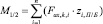 , (6)
, (6)
где ω – коэффициент эксцентриситета;
e1 – предельный эксцентриситет, мм;
e2 – эксцентриситет металлических накладок, мм;
e3 – эксцентриситет изгиба, мм;
F – несущая способность соединения SHERPA при изгибе, Н;
M – изгибающий момент, Н∙мм;
M1/2 – изгибающий момент, действующий на алюминиевые накладки, Н∙мм;
Fax,k,i – несущая способность шурупа на выдергивание, Н.
Для получения экспериментальных значений нормативной прочности в механической лаборатории СПбГАСУ проведены испытания на изгиб с использованием универсальной испытательной машины INSTRON 5969 (максимальный режим работы до 50 кН) и INSTRON 5989 (максимальный режим работы до 600, кН). Режим нагружения при непрерывном увеличении нагрузки 2 мм/мин.
Поскольку в работах автора использована конструкция «балка из LVL (брус из клееного шпона) и стеновая панель из CLT (панель из поперечно-клееной древесины)», нужно определить плотности материалов из CLT и LVL. Температура в лаборатории 20 ± 1 °C и влажность материалов 13 %. На основе полученных из испытания результатов плотность определяется равной 495 кг/м3 для CLT и 560 кг/м3 для LVL.
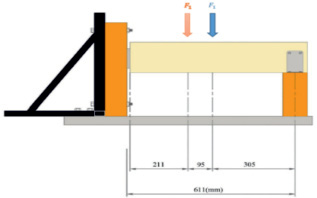
Расположение металлических накладок в деревянных конструкциях и установка опытных деревянных образцов на экспериментальном стенде представлены на рис. 2.
а)
б)
Рис. 2. Испытание соединения SHERPA на изгиб: а – расположение соединения SHERPA; б – установка деревянных опытных образцов на экспериментальном стенде
Из рис. 2 видно, что деревянная опытная балка крепится двумя заделанными концами. С учетом использования литературы [5] и диссертационной работы автора, сравнения экспериментальных и расчётных результатов определения несущей способности соединения SHERPA при изгибе без укрепления и с МЗП (металлические зубчатые пластины) с учётом коэффициента эксцентриситета представлены в табл. 1 и 2.
Из [4] несущая способность соединения SHERPA при изгибе без учёта коэффициента эксцентриситета равна 15000 Н, коэффициент эксцентриситета с учётом физико-механических и геометрических характеристик деревянных опытных материалов составляет 0,5. Сравнения расчётных и экспериментальных результатов определения несущей способности соединения SHERPA без укрепления и с МЗП с учётом коэффициентов эксцентриситета при изгибе в деревянных конструкциях из комбинации стеновой панели-CLT с балкой из СLT и LVL представлены в табл. 3 и 4 в соответствии с графиками (рис. 3 и 4).
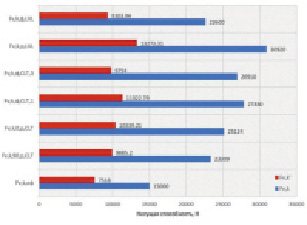
Рис. 3. Сравнение расчётных и экспериментальных результатов определения несущей способности соединения SHERPA при изгибе без учёта коэффицента эксцентриситета без укрепления МЗП
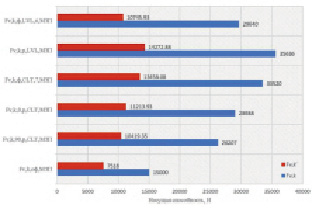
Рис. 4. Сравнение расчётных и экспериментальных результатов определения несущей способности соединения SHERPA при изгибе без учёта коэффицента эксцентриситета с укреплением МЗП
Таблица 1
Сравнение расчётных и экспериментальных результатов определения несущей способности соединения SHERPA при изгибе без учёта коэффицента эксцентриситета с укреплением МЗП
|
На широкой стороне панели-CLT |
На узкой стороне панели из CLT |
Вдоль волокон балки из LVL |
||||||
|
Fv,ф,CLT,МЗП |
Fv,р,CLT,МЗП |
μ |
Fv,ф,CLT,МЗП |
Fv,р,CLT,МЗП |
μ |
Fv,ф,CLT,МЗП |
Fv,р,CLT,МЗП |
μ |
|
33520 |
29234 |
14,66 % |
33520 |
31556 |
6,22 % |
29640 |
36764 |
– 19,38 % |
Примечания. Fv,ф,CLT,МЗП – фактическая несущая способность с
укреплением МЗП, Н; Fv,р,CLT,МЗП – расчётная несущая способность с
укреплением МЗП, Н; μ – приращение Fv,ф,CLT,МЗП и Fv,р,CLT,МЗП;  .
.
Таблица 2
Сравнение расчётных и экспериментальных результатов определения несущей способности соединения SHERPA при изгибе без учёта коэффицента эксцентриситета без укрепления МЗП
|
На широкой стороне панели-CLT |
На узкой стороне панели-CLT |
Вдоль волокон балки из LVL |
||||||
|
Fv,ф,CLT |
Fv,р,CLT |
μ |
Fv,ф,CLT |
Fv,р,CLT |
μ |
Fv,ф,CLT |
Fv,р,CLT |
μ |
|
27830 |
26331 |
5,69 % |
26910 |
27684 |
– 2,80 % |
22600 |
32036 |
– 29,45 % |
Примечания. Fv,ф,CLT – фактическая несущая способность без
укрепления МЗП, Н; Fv,р,CLT – расчётная несущая способность без
укрепления МЗП, Н; μ – приращение Fv,ф,CLT и Fv,р,CLT;  .
.
Таблица 3
Сравнение расчётных и экспериментальных результатов определения несущей способности соединения SHERPA при изгибе без и с учётом коэффицента эксцентриситета без укрепления МЗП
|
Параметр |
Fv,k,оф |
Fv,k,90,р,CLT |
Fv,k,0,р,CLT |
Fv,k,ф,CLT,1 |
Fv,k,ф,CLT,3 |
Fv,k,р,LVL |
Fv,k,ф,LVL |
|
Fv,k |
15000 |
26331 |
27684 |
27830 |
26910 |
32036 |
22600 |
|
μ |
– |
75,54 % |
84,56 % |
85,53 % |
79,40 % |
113,57 % |
50,67 % |
|
ω |
0,50 |
0,41 |
0,40 |
0,41 |
0,36 |
0,42 |
0,41 |
|
Fv,k’ |
7518,00 |
10795 |
11073 |
11322 |
9753 |
13455 |
9303 |
|
μ’ |
– |
43,94 % |
47,65 % |
50,97 % |
30,05 % |
79,40 % |
24,05 % |
Примечания. Fv.k – несущая способность на срез без учёта
коэффициента эксцентриситета, Н; Fv,k’ – несущая способность на срез с
учётом коэффициента эксцентриситета, Н; μ – приращение Fр/ф и Fv,k,оф;  ; μ’ – приращение Fр/ф’ и Fалю’;
; μ’ – приращение Fр/ф’ и Fалю’;  .
.
Таблица 4
Сравнение расчётных и экспериментальных результатов определения несущей способности соединения SHERPA при изгибе без и с учётом коэффицента эксцентриситета с с укреплением МЗП
|
Параметр |
Fv,k,оф,МЗП |
Fv,k,90,р,CLT,МЗП |
Fv,k,0,р,CLT,МЗП |
Fv,k,ф,CLT,7,МЗП |
Fv,k,р,LVL,МЗП |
Fv,k,ф,LVL,6,МЗП |
|
Fv,k |
15000 |
29234 |
31556 |
33520 |
36764 |
29640 |
|
μ |
– |
94,89 % |
110,37 % |
123,47 % |
145,09 % |
97,60 % |
|
ω |
0,50 |
0,39 |
0,38 |
0,40 |
0,40 |
0,36 |
|
Fv,k’ |
7518,00 |
11401 |
11991 |
13408 |
14705 |
10670 |
|
μ’ |
– |
52,02 % |
59,88 % |
78,77 % |
96,07 % |
42,27 % |
Примечания. Fv.k – несущая способность на срез без учёта
коэффициента эксцентриситета, Н; Fv,k’ – несущая способность на срез с
учётом коэффициента эксцентриситета, Н; μ – приращение Fр/ф и Fv,k,оф;  ; μ’ – приращение Fр/ф’ и Fалю’;
; μ’ – приращение Fр/ф’ и Fалю’;  .
.
Из табл. 3 видно, что коэффициент эксцентриситета, определяемый по предложенным уравнениям, достаточно близок к данному коэффициенту 0,5 [4]. Полученные расчётные и экспериментальные результаты, умножаемые на коэффициент ω, не только соответствуют нормативной несущей способности 7518 Н, но и незначительно превышают её, потому что нормативная несущая способность для соединения SHERPA S15 при изгибе должна удовлетворять условию консервативности для различных типов деревянных материалов при конструировании. Методика для расчёта коэффициента эксцентриситета [4], разработанная руководством компании SHERPA, в соответствии с исследованием автора может быть усовершенствована. При этом должна быть выполнена:
• корректировка неопределённых понятий для коэффициента эксцентриситета на основе данной методики;
• предложен новый численный алгоритм;
Из табл. 4 видно, что расчётные и экспериментальные результаты для соединения SHERPA выше максимально на 113,57 % и минимально на 50,67 %, чем нормативное значение 15000 Н, а после умножения на коэффициент эксцентриситета выше максимально на 79,40 % и минимально на 24,05 %, чем 7518 Н. Сравнительный анализ показывает, что предложенный численный алгоритм для расчёта коэффициента эксцентриситета может обеспечить и повысить достоверность и надёжность конструирования.
Выводы
1. Рассматривается возможность применения соединения SHERPA в большепролетных деревянных конструкциях из комбинации стеновой панели-CLT с балкой из CLT и CLT.
2. Предложен численный алгоритм для определения коэффициента эксцентриситета на основе [4].
3. Теоретически модели проверены и экспериментально показано влияние эксцентриситета на несущую способность соединения SHERPA при изгибе на основе сравнительного анализа, подтверждена эффективность использования коэффициента эксцентриситета для повышения надёжности и безопасности конструирования.
4. По сравнению с традиционным алгоритмом выполнена корректировка неопределенных понятий и повышение точности расчёта.
Рецензенты:Глухих В.Н., д.т.н., профессор, заведующий кафедрой технической механики, ФГБОУ ВПО «Санкт-Петербургский государственный архитектурно-строительный университет», г. Санкт-Петербург;
Черных А.Г., д.т.н., профессор, академик Российской академии естественных наук (РАЕН), проректор СПГХПА, г. Санкт-Петербург.
Работа поступила в редакцию 02.02.2015.



