Динамическая голография – одно из перспективных направлений развития современной нелинейной оптики. В классической (статической) голографии запись голографической решетки (голограммы) в регистрирующей среде и восстановление записанной волны (изображения) считывающим излучением совершаются поэтапно. В случае динамической голографии эти процессы могут происходить одновременно – «в реальном времени». Это отличие значительно расширяет возможности применения голографии для управления пространственно-временной структурой излучения. Хотя основные принципы динамической голографии сформулированы относительно недавно, быстрое ее развитие уже привело к значительным результатам в таких, например, областях, как оптическая обработка информации, оптическая связь, управление световыми потоками [7]. На основе динамических голографических преобразователей создаются логические элементы ЭВМ с быстродействием до 10-12 с, системы оперативной памяти, управляемые транспаранты, оптические переключатели, ответвители и др. устройства оптоэлектроники, оптические корреляторы, служащие для голографического распознавания образов и т.д. [7].
Механизмы нелинейности сред, используемые для записи динамических голограмм, весьма разнообразны [1–8]. Наибольшие значения c(3) обеспечивают резонансные нелинейности – насыщение поглощения в газах, насыщение межзонного перехода в полупроводниках [7]. Однако применение этих механизмов нелинейности ограничено узким спектральным диапазоном. Свободным от этого недостатка и более перспективными с точки зрения использования многочастотного излучения являются среды с нерезонансной нелинейностью. Механизмы этого типа обеспечивают достаточную высокую эффективность нелинейного взаимодействия импульсного излучения в видимом и ИК-диапазонах спектра [1]. Наиболее актуально исследование указанного класса сред, обладающих большой нерезонансной термоиндуцированной нелинейностью, для ИК-диапазона спектра, где отсутствуют эффективные фоточувствительные механизмы нелинейности, успешно «работающие» в видимой части спектра и источники когерентного излучения в котором обладают, как правило, сложным и нестабильным спектральным составом.
Целью данной работы является сравнительный анализ различных механизмов нелинейности сред с точки зрения эффективности записи динамических голограмм.
Голографическая чувствительность
Обычно принято сравнивать различные среды и механизмы нелинейности по величине нелинейной восприимчивости третьего порядка c(3), характеризующего кубичный нелинейный отклик. В случае нерезонансной нелинейности (для слабопоглощающих сред) чаще используют другой параметр n2 = (∂n/∂I), который связан с c(3): n2[см2/кВт] = (2p/n0)2c(3) ед. СГСЕ. Однако использование только этого параметра часто не позволяет провести корректное сравнение и тем более оценить максимальные величины эффективности записи динамической голограммы. В большинстве случаев (и в первую очередь для тепловых нелинейностей) величина квазистационарного c(3) пропорциональна времени релаксации нелинейного отклика τ, т.е. зависит от геометрии схемы и условий эксперимента.
Поэтому для оценки эффективности записи динамической голограммы, наряду с n2, мы предлагаем использовать более информативный параметр – голографическую чувствительность по энергии [7]
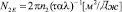 , (1)
, (1)
где a – коэффициент поглощения среды, l – длина волны излучения. Последний параметр учитывает ещё и тот фактор, что эффективность голограммы зависит от её толщины, которая ограничена поглощением или рассеянием среды (обычно величина c(3) ~ a), и длины волны излучения. Для объемной голограммы величина данного параметра соответствует минимальной энергии записывающего излучения, необходимой для изменения оптической толщины слоя среды на длину волны излучения и прямо характеризует дифракционную эффективность голограммы.
Дифракционной эффективностью голограммы называется отношение [7]
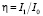 , (2)
, (2)
где I0 – интенсивность падающего на голограмму считывающего луча; I1 – интенсивность света, продифрагировавшего в первый порядок дифракции на голограмме, представляющей собой обычно простую косинусоидальную решетку. Легко увидеть, что, например, для тонких амплитудно-фазовых голограмм параметр N2E однозначно характеризует дифракционную эффективность [7].
Более того, размерность введенной чувствительности N2E позволяет сравнивать как объемные, так и поверхностные механизмы нелинейности [7, 11]. Для последних голографическая чувствительность по энергии определяется как
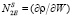 , (4)
, (4)
где r – амплитудный френелевский коэффициент отражения излучения границей раздела сред, W = Iτ – энергия импульса записывающего излучения.
Термоиндуцированные нелинейности однокомпонентных сред
Тепловая нелинейность является универсальной и существует в любой среде, поглощающей излучение. Для однокомпонентных сред простейший механизм нелинейности обусловлен тепловым расширением среды. При этом обычно используется запись фазовых голограмм, основанная на модуляции показателя преломления [1, 4, 5]. Выражение для коэффициента эффективной кубичной нелинейности можно получить, решая одномерное уравнение теплопроводности (учитывая, что n2 = (∂n/∂T)(∂T/∂I) [7]:
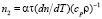 , (5)
, (5)
где (dn/dT) – температурный коэффициент показателя преломления, cp и r – удельные теплоемкость и плотность среды. Параметр голографической чувствительности N2E находим из (1):
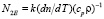 . (6)
. (6)
Таким образом, величина тепловой нелинейности однокомпонентных сред определяется параметрами (dn/dT), cp, r.
Подставляя характерные параметры для полупроводниковых сред dn/dT = 2·10-4K-1, (cpr) ≈ 1 Дж/см3К, получаем (для излучения с длиной волны l = 10 мкм) N2E = 1 см2/Дж. Параметр (∂n/∂T) немного больше для большинства органических жидкостей и составляет (4÷7)10-4 К-1. Подставляя характерные значения для жидкостей (cpr) ≈ 1 Дж/см3К, dn/dT = 5·10-4K-1, получаем N2E = 3 см2/Дж, что несколько выше, чем для твердотельных сред. Рекордной величиной (∂n/∂T) обладают нематические жидкие кристаллы (НЖК) – вблизи фазового перехода (∂n/∂T) может достигать 10-2К-1 [7]. Однако для эффективной записи динамических голограмм излучением с интенсивностью в несколько мВт/см2 требуются среды с большей величиной коэффициента нелинейности.
Микрогетерогенные среды
Тенденция перехода к микрогетерогенным средам в направлении поиска больших нелинейностей прослеживается достаточно легко. Если в первых работах использовались нелинейные среды с типичной величиной n2 ~ 10-13 см2/Вт (например, молекулярная керровская нелинейность), то сейчас в микроэмульсиях экспериментально достигнуты величины n2 ~ 10-6см2/Вт (электрострикционная нелинейность) [3, 7, 8–10]. Многокомпонентные дисперсные среды (жидкофазные смеси, суспензии, эмульсии) характеризуются наличием целого ряда специфических механизмов нелинейности, которые отсутствуют в однокомпонентных средах. В частности, к ним относятся концентрационные нелинейности, обусловленные перераспределением компонент двухфазной среды в поле лазерного излучения. При этом концентрационные потоки в среде могут вызываться различными механизмами взаимодействия излучения с веществом.
Параметр эффективной нелинейности оценим следующим образом. В микрогетерогенной среде с частицами радиуса, много меньше длины волны излучения l, показатель преломления среды пропорционален концентрации частиц [7]:
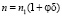 , (7)
, (7)
где d = (n2 – n1)/nq; n2,n1 – показатели преломления вещества дисперсионной среды и дисперсной фазы соответственно, j = (4/3)pr3C – объемная доля дисперсной среды, r – радиус микрочастиц. Тогда для любого концентрационного механизма нелинейности имеем:
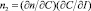 . (8)
. (8)
К термоиндуцированным механизмам дрейфа частиц в неоднородном температурном поле относятся термодиффузия (термофорез) в газах, суспензиях, эффект Соре в жидкофазных бинарных смесях [2, 7, 14]. В микрогетерогенной среде с различными показателями преломления компонентов на микрочастицы в электромагнитном поле действуют электрострикционные силы, которые также могут быть причиной возникновения концентрационных потоков [8–10, 13]. В зависимости от знака поляризуемости микрочастицы могут втягиваться (если показатель преломления вещества дисперсной фазы больше, чем дисперсионной среды) или выталкиваться (в обратном случае) из областей с большей напряженностью электрического поля Е электромагнитной волны.
В работе [7] получено выражение для голографической чувствительности дисперсной среды с учетом обоих концентрационных механизмов:
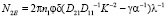 . (9)
. (9)
При этом термоиндуцированная нелинейность жидкофазной двухкомпонентной среды определяется коэффициентами термодиффузии и диффузии (D21, D11) – 1-е слагаемое, а электрострикционная – поляризуемостью микрочастицы g (2-е слагаемое). Как видно из (9), оба механизма могут либо усиливать либо ослаблять друг друга в зависимости от знаков коэффициента термодиффузии и поляризуемости дисперсных частиц. Полученное выражение демонстрирует чувствительность термодиффузионного нелинейного механизма к пространственной частоте голографической решетки (в отличие от тепловой нелинейности однокомпонентных сред). Как показывают оценки и результаты экспериментальных работ для обоих концентрационных нелинейностей параметр голографической чувствительности может достигать N2E ≈ 10 – 100 см2/Дж.
Заключение
Проведенный выше анализ позволяет сделать следующие выводы. Для большинства нерезонансных механизмов параметр кубичной нелинейности n2 пропорционален времени релаксации. Так как время релаксации (например, время концентрационной или вращательной диффузии) возрастает с увеличением размеров частицы, то естественно ожидать больших параметров нелинейности в микрогетерогенных средах (суспензии, микроэмульсии), максимальный размер частиц в которых ограничен длиной волны излучения из-за светорассеяния.
Величина нелинейности не является единственным показателем, определяющим качество материала, так как основные параметры, как правило, взаимосвязаны: например, большое значение нелинейности обычно соответствует плохому временному разрешению, пространственное разрешение и чувствительность голографических сред также находятся в обратной зависимости (данный факт хорошо известен в обычной галоидосеребряной фотографии). Поскольку параметры известных материалов образуют дискретный набор, возникает проблема выбора среды с характеристиками, оптимальными для конкретного применения. Наиболее перспективны в этом смысле гетерогенные среды, очевидное преимущество которых, в частности, состоит в возможности изменения объемной доли различных компонент и их состава, то есть управления (в том числе в реальном масштабе времени) параметрами. Учитывая многообразие известных механизмов нелинейности и особенности их проявления в гетерогенных системах, а также то, что по величине голографической чувствительности такие материалы приближаются к полупроводниковым, можно выделить их в новый перспективный класс сред для динамической голографии.
Рецензенты:
Карпец Ю.М., д.ф.-м.н., профессор, профессор кафедры «Физика и теоретическая механика», ДВГУПС, г. Хабаровск;
Криштоп В.В., д.ф.-м.н., профессор, заведующий кафедрой «Физика и теоретическая механика», ДВГУПС, г. Хабаровск.
Работа поступила в редакцию 31.12.2014.



