Изложение даётся на примере системы дифференциальных уравнений цилиндрической оболочки ракеты – системы обыкновенных дифференциальных уравнений 8-го порядка (после разделения частных производных методом Фурье) [5].
Система линейных обыкновенных дифференциальных уравнений имеет вид
,
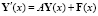где Y(x) – искомая вектор-функция задачи размерности 8×1, Y’(x) – производная искомой вектор-функции размерности 8×1, A – квадратная матрица коэффициентов дифференциального уравнения размерности 8×8, F(x) – вектор-функция внешнего воздействия на систему размерности 8×1.
Краевые условия имеют вид:
, 
,
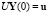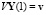где Y(0) – значение искомой вектор-функции на левом крае х = 0 размерности 8×1, U – прямоугольная горизонтальная матрица коэффициентов краевых условий левого края размерности 4×8, u – вектор внешних воздействий на левый край размерности 4×1, Y(1) – значение искомой вектор-функции на правом крае х = 1 размерности 8×1, V – прямоугольная горизонтальная матрица коэффициентов краевых условий правого края размерности 4×8, v – вектор внешних воздействий на правый край размерности 4×1.
В случае, когда система дифференциальных уравнений имеет матрицу с постоянными коэффициентами A = const, решение задачи Коши имеет вид [2]
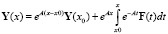
где e A(x – x0) = E + A(x – x0) + A2(x – x0)2/2! + A3 (x – x0)3/3! + …, где E – это единичная матрица.
Матричная экспонента ещё может называться матрицей Коши или матрициантом и может обозначаться в виде
.
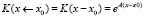Тогда решение задачи Коши может быть записано в виде
,
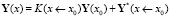где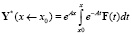 
– это вектор частного решения неоднородной системы дифференциальных уравнений.
Из теории матриц [1] известно свойство перемножаемости матричных экспонент (матриц Коши)
.
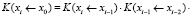
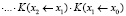В случае, когда система дифференциальных уравнений имеет матрицу с переменными коэффициентами A = A(x), решение задачи Коши можно (как это известно из теории матриц) искать при помощи свойства перемножаемости матриц Коши. То есть интервал интегрирования разбивается на малые участки, и на малых участках матрицы Коши приближенно вычисляются по формуле для постоянной матрицы в экспоненте. А затем матрицы Коши, вычисленные на малых участках, перемножаются:
,
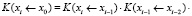
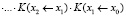где матрицы Коши приближенно вычисляются по формуле
,
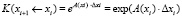где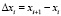 
.
Вместо формулы для вычисления вектора частного решения неоднородной системы дифференциальных уравнений в виде [1]
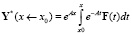
предлагается использовать следующую формулу для каждого отдельного участка интервала интегрирования:
.
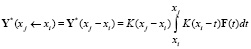Правильность приведенной формулы подтверждается следующим:
,
,
, 
,
, 
,
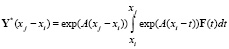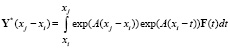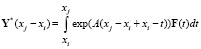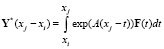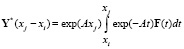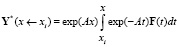что и требовалось подтвердить.
Вычисление вектора частного решения неоднородной системы дифференциальных уравнений производится при помощи представления матрицы Коши под знаком интеграла в виде ряда и интегрирования этого ряда поэлементно:
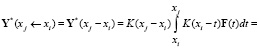
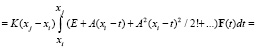
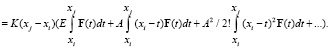
Эта формула справедлива для случая системы дифференциальных уравнений с постоянной матрицей коэффициентов A = const. Вектор F(t) может рассматриваться на участке (xj – xi) приближенно в виде постоянной величины F(xi) = constant, что позволяет вынести его из под знака интеграла, что приводит к совсем простому ряду для вычислений на рассматриваемом участке. Для случая дифференциальных уравнений с переменными коэффициентами в приведенной выше формуле для каждого участка может использоваться осредненная матрица Ai = A(xi) коэффициентов системы дифференциальных уравнений. Рассмотрим вариант, когда шаги интервала интегрирования выбираются достаточно малыми, что позволяет рассматривать вектор F(t) на участке (xj – xi) приближенно в виде постоянной величины F(xi) = constant, что позволяет вынести этот вектор из под знаков интегралов:
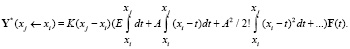
Известно, что при T = (at + b) имеем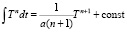 
(при n ≠ –1).
В нашем случае имеем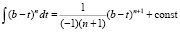 
(при n ≠ –1).
Тогда получаем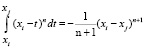 
.
Тогда получаем ряд для вычисления вектора частного решения неоднородной системы дифференциальных уравнений на малом участке (xj – xi)
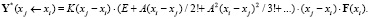
Если участок (xj – xi) не мал, то его можно поделить на подучастки и тогда можно предложить следующие рекуррентные (итерационные) формулы для вычисления частного вектора.
Имеем
.
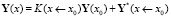Также имеем формулу для отдельного подучастка
.
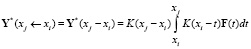Можем записать
,
.
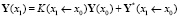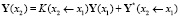Подставим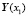 
в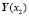 
и получим
.
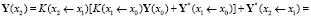
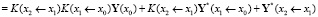Сравним полученное выражение с формулой
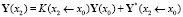
и получим, очевидно, что
,
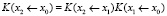и для частного вектора получаем формулу
.
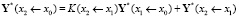То есть вектора подучастков Y*(x1 ← x0), Y*(x2 ← x1) не просто складываются друг с другом, а с участием матрицы Коши подучастка. Аналогично запишем Y(x3) = K(x3 ← x2)Y(x2) + Y*(x3 ← x2) и подставим сюда формулу для Y(x2) и получим
.
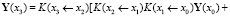
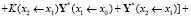
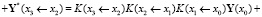
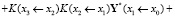
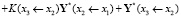Сравнив полученное выражение с формулой
,
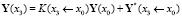очевидно, получаем, что
,
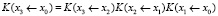и вместе с этим получаем формулу для частного вектора
.
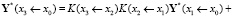
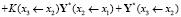То есть именно так и вычисляется частный вектор – вектор частного решения неоднородной системы дифференциальных уравнений, то есть так вычисляется, например, частный вектор Y*(x3 ← x0) на рассматриваемом участке (x3 ← x0) через вычисленные частные вектора Y*(x1 ← x0), Y*(x2 ← x1), Y*(x3 ← x2) соответствующих подучастков (x1 ← x0), (x2 ← x1), (x3 ← x2).
Контроль точности вычислений. В случае использования описанной кусочно-константной аппроксимации матрицы системы обыкновенных дифференциальных уравнений (ОДУ) с переменными коэффициентами, когда на всем интервале интегрирования системы ОДУ используются матричные экспоненты от осредненных постоянных аргументов, оценка точности теоретически не дается и предлагаемый метод в этом частном случае можно считать «инженерным», который дает достаточно точные решения для уже опробованных инженерных задач. В тоже время можно производить вычисления и иначе – с заранее известной точностью. В таком варианте предлагаемого метода – в случае применения методов типа Рунге-Кутты для вычисления матриц Коши – хорошо известны оценки точности приближенных вычислений, что означает, что вычисления можно производить с заранее известной погрешностью, так как оценки погрешностей методов Рунге-Кутты известны.
Простейший метод решения жестких краевых задач. Идея преодоления трудностей решения жёстких краевых задач путём разделения интервала интегрирования на сопрягаемые участки принадлежит д.ф.-м.н. Ю.И. Виноградову, а выражение этого сопряжения через формулы теории матриц принадлежит к.ф.-м.н. А.Ю. Виноградову. Разделим интервал интегрирования краевой задачи, например, на 3 участка. Будем иметь точки (узлы), включая края:
.
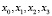Имеем краевые условия в виде
,
.
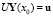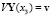Можем записать матричные уравнения сопряжения участков:
,
,
.
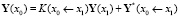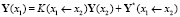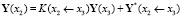Это мы можем переписать в виде, более удобном для нас далее:
,
,
.
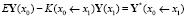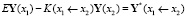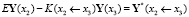где Е – единичная матрица.
Тогда в объединенном матричном виде получаем систему линейных алгебраических уравнений в следующей форме:
.
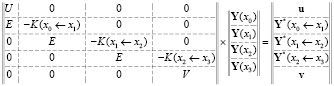Эта система решается методом Гаусса с выделением главного элемента. В точках, расположенных между узлами, решение находиться при помощи решения задач Коши с начальными условиями в i-ом узле
.
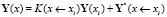Применять ортонормирование для краевых задач для жестких обыкновенных дифференциальных уравнений в рамках предложенного метода, оказывается, не надо.
И так как предлагаемый метод на каждом отдельном участке интервала интегрирования реализуется от единичной (ортонормированной) матрицы, то нет необходимости в программировании процедур ортонормирования, в отличие от метода С.К. Годунова, что делает программирование предлагаемого метода гораздо более простым по сравнению с методом С.К. Годунова [4].
Вычислительные эксперименты. Вычислительные эксперименты проводились в сравнении с методом Виноградовых [1] переноса краевых условий. В этом методе используется построчное ортонормирование. Новый предлагаемый здесь метод позволяет решать все вышеуказанные тестовые задачи вовсе без применения операций ортонормирования, что значительно упрощает его программирование [3]. Для тестовых расчетов задач с вышеуказанными параметрами новым предлагаемым методом интервал интегрирования разделялся на 10 участков, а между узлами, как и сказано выше, решение находилось как решение задачи Коши. Для решения задач удерживалось 50 гармоник рядов Фурье, так как результат при 50 гармониках уже не отличался от случая удержания 100 гармоник. Скорость же расчета тестовых задач новым предлагаемым методом не меньше, чем методом переноса краевых условий, так как оба метода в тестовых задачах при удержании 50 гармоник рядов Фурье выдавали готовое решение мгновенно после запуска программы на выполнение (на ноутбуке ASUS M51V CPU Duo T5800). В то же время программирование нового предложенного здесь метода существенно проще, так как нет необходимости программировать процедуры ортонормирования.
Рецензенты:
Гейнович И.Ю., д.ф.-м.н., профессор, НП «Южный инновационно-технологический университет», г. Ростов-на-Дону;
Предеина Л.М., д.ф.-м.н., профессор, ФГБУ «Гидрохимический институт» Росгидромета, г. Москва.
Работа поступила в редакцию 31.12.2014.