Изменения, происходящие в высшей профессиональной школе, требуют ориентации образовательного процесса на становление таких важных личностных качеств выпускников, как настойчивое стремление к непрерывному самообразованию, установка на постоянное пополнение имеющихся знаний новыми, расширяющими сферу их возможного применения на практике. Большое значение приобретает способность ориентироваться в информационных потоках, умение быстро находить полезную информацию, анализировать её и использовать в своей деятельности, повышая эффективность интеллектуального или физического труда, склонность к самостоятельному принятию решений, творческое отношение к учебной или профессиональной деятельности.
Всё это актуализирует проблему развития познавательной самостоятельности студентов в обучении, делает необходимым поиск новых путей и методических средств её решения как при изучении отдельных учебных дисциплин, так и в постановке педагогической деятельности в рамках всего образовательного процесса.
Соглашаясь с мнениями передовых педагогов (В.М. Монахова, С.В. Панюковой, Н.А. Максимовой, Е.Н. Вороновой и др., мы предприняли попытку органического синтеза сильных сторон современных задачных и информационных технологий для создания подхода к совершенствованию образовательного процесса в высшей (педагогической) школе, суть которого состоит в том, чтобы выполнению учебных заданий придать дополнительные стимулы и смыслы, а учебное познание облечь в такие формы деятельности, которые притягательны для студентов, созвучны их внутренним устремлениям, отвечают духу времени, побуждают совершать благородные поступки [4, 5, 6, 9].
Речь идёт об использовании с целью развития их познавательной самостоятельности возможностей образовательных Web-квестов. Наш выбор определён тематическими образовательными Web-квестами, под которыми понимаем такой Web-квест, который имеет информационный контент, определяющийся содержанием учебной темы, целями и задачами заключительного этапа её изучения и предполагает выполнение заданий с использованием Интернет-ресурсов, способствующих развитию познавательной самостоятельности учащихся.
Его информационный контент включает в себя пять основных компонентов: теория (дополнительная информация, учебно-познавательные задания, позволяющие углубить имеющие знания, получить целостное представление об их месте и роли в изучаемой теории), приложения (сведения и учебно-познавательные задания, расширяющие представления о возможных применениях изученного в учебной теме математического аппарата), проблемы (информация и учебно-познавательные задания исследовательского характера, позволяющие отыскивать или открывать неизвестные учащимся факты, закономерности, свойства, формулы или сведения, связанные с учебным материалом изученной темы), архивы (сведения историко-биографического характера, касающиеся учебного материала темы, и учебно-познавательные задания по их упорядочиванию, хронологическому или сюжетному представлению) и ошибки (информация о больших и малых заблуждениях, курьёзных случаях, распространённых или единичных ошибках по учебному материалу темы, имевших место когда-либо или с кем-либо, а также учебно-познавательные задания по их анализу и отысканию возможных путей предупреждения), которые охватывают наиболее значимые направления методической работы [3, 7].
Наполнение указанных компонентов информационного контента тематического образовательного Web-квеста определяют, прежде всего, поисково-познавательные задания, они образуют задачную конструкцию особого рода, имеющую своё композиционное построение, функциональную направленность и лексическую форму [8].
Особенности поисково-познавательных заданий во многом определяются основными положениями деятельностного подхода к обучению математике, утвердившемуся в методической науке, в контексте которого решение задач является видом учебной деятельности, обеспечивающим и усвоение учащимися математического содержания, и формирование умений и навыков, и достижение развивающих целей образования. По мнению ряда современных отечественных педагогов-математиков (Я.И. Груденов, М.И. Зайкин, О.А. Иванов, Т.А. Иванова, Г.И. Саранцев, Л.М. Фридман, П.М. Эрдниев и др.), эффективность учебной работы напрямую определяется тем, какие именно задачи и в какой последовательности предлагались учащимся, какими способами они решались и как велика была доля активности, самостоятельности учеников в процессе их решения. Но главное все же – это сами задачи, а точнее задачные конструкции (системы, циклы, блоки, цепочки, серии и т.п.), подготовленные учителем или методистом к занятию [10].
Как говорилось выше, задачные конструкции, задействуемые в профессиональной подготовке студентов вузов, должны соответствовать современным требованиям, предъявляемым к выпускникам, а потому предоставлять им возможность развития познавательной самостоятельности в большей степени, чем ранее. Прежде всего, это касается подготовки педагогических кадров, способных привносить полученные результаты в систему школьного, в частности, математического образования. В связи с этим следует говорить об использовании возможностей Web-квест технологий на занятиях по основным методическим дисциплинам, в том числе практикума по решению задач школьной математики, который относится к вариативной части профессионального цикла. Основными целями её освоения являются формирование систематизированных знаний, умений и навыков в области элементарной математики, создание необходимой теоретической базы для решения школьных математических задач.
Процесс изучения этой дисциплины направлен на формирование следующих компетенций: владением культурой мышления, способностью к обобщению, анализу, восприятию информации, постановке цели и выбору путей её достижения; способностью использовать знания о современной естественнонаучной картине мира в образовательной и профессиональной деятельности, применять методы математической обработки информации, теоретического и экспериментального исследования; способностью работать с информацией в глобальных компьютерных сетях; осознанием социальной значимости своей будущей профессии, обладанием мотивацией к осуществлению профессиональной деятельности; владением основами речевой профессиональной культуры; способностью разрабатывать и реализовывать учебные программы базовых и элективных курсов в различных образовательных учреждениях.
В результате изучения дисциплины студент должен: знать основные понятия школьного курса математики, с точки зрения заложенных в них фундаментальных математических идей; современные направления развития элементарной математики и их приложения; литературу по элементарной математике (учебники и сборники задач, книги и т.д.); уметь работать в школе по различным учебникам математики; работать в классах различной профильной направленности и индивидуальной работы с учащимися; проводить со школьниками кружки, спецкурсы, факультативные занятия и олимпиады по математике; владеть важнейшими методами элементарной математики, уметь применять их для доказательства теорем и решения задач. В соответствии с этим в содержание дисциплины включены следующие разделы: арифметика, прогрессии, текстовые задачи, элементы стохастики и избранные олимпиадные задачи.
Для достижения указанной цели и решения поставленных задач настоящее пособие в своей структуре сочетает современные методические тенденции задачной технологии и интерактивного обучения студентов, обучающихся по направлению педагогическое образование [1, 2]. Каждое занятие построено на основе синтеза традиционного практикума, современных задачных подходов, базирующихся на окрестностях обобщенных математических задач, а также организации самостоятельной познавательной деятельности студентов посредством использования Web-квест технологий. В соответствии с этим в структуре занятий выделены четыре основные части: теоретический базис, ключевые задачи, окрестности задач и задания тематического образовательного Web-квеста (проиллюстрированы на примере темы «Арифметическая прогрессия и её свойства»).
Теоретический базис
Определение: Числовая последовательность, каждый член которой, начиная со второго, равен предыдущему, сложенному с одним и тем же числом, называется арифметической прогрессией. При этом постоянное слагаемое называют разностью арифметической прогрессии d = an – an–1.
Формула n-го члена арифметической прогрессии:, an = a1 + d(n – 1), где a1 – первый член прогрессии, an – n-й член арифметической прогрессии, n – номер члена прогрессии (n ∈ N), d – ее разность.
Свойство арифметической прогрессии: Каждый член арифметической прогрессии, начиная со второго, равен среднему арифметическому двух соседних с ним членов, т.е.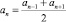 
(n ≥ 2).
Замечание: Можно обобщить свойство арифметической прогрессии, т.е. сформулировать следующим образом – каждый член арифметической прогрессии, начиная со второго, равен среднему арифметическому двух ее членов, одинаково удаленных от него,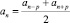 
(n ≥ 2).
Ключевые задачи
Задания на применение формулы n-го члена арифметической прогрессии, ее свойства в различных формулировках, сюжетные задачи на применение самого понятия арифметической прогрессии.
Задача 1. Найдите двадцатый член арифметической прогрессии, если ее седьмой член равен 18, а двенадцатый член равен –2.
Решение:
Применим формулу n-го члена арифметической прогрессии для седьмого и двенадцатого членов прогрессии: a7 = a1 + 6d, a12 = a1 + 11d. Подставляя в равенства заданные значения, получим систему двух уравнений с двумя неизвестными (а1 и d):
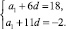
Решением этой системы являются значения а1 = 42 и d = –4.
Используя формулу n-го члена арифметической прогрессии и подставляя в неё найденные значения а1 и d, найдем двадцатый член прогрессии
a20 = a1 + 19d = 42 – 76 = –34.
Задача 2. Сумма пятого и семнадцатого членов арифметической прогрессии равна –200. Какой член прогрессии можно найти? Чему равно его значение?
Решение:
В указанной арифметической прогрессии одинаково удаленным от пятого и семнадцатого членов является одиннадцатый ее член, его значение можно найти, используя обобщенную формулировку свойства арифметической прогрессии
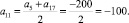
Задача 3. Мама составляет коллекцию комнатных растений. Каждый месяц она увеличивает количество приобретаемых цветов на 2. Сколько цветов она купит в десятый раз, если первая покупка составляла 3 цветка?
Решение:
Поскольку каждый раз количество приобретаемых растений увеличивается на одно и тоже число, значит, говорится об арифметической прогрессии, при чем первый ее член равен 3, а разность равна 2. Тогда применяем формулу n-го члена арифметической прогрессии и получаем, что
a10 = a1 + 9d = 3 + 18 = 21.
Окрестности задач
Окрестности обобщенных задач можно получить путем увеличения числа требований задач, их обобщения через нахождение различных способов задания арифметической прогрессии.
№ 1. Запишите формулу n-го члена арифметической прогрессии, если ее третий член равен 1,2; а седьмой член равен 3,8.
№ 2. Петя ежедневно увеличивает число покупаемых марок на 3. На седьмой день он купил 19 штук. Сколько марок купил Петя в первый день? Сколько он купит в 11 день? В какой день он купил семь марок?
№ 3. Известно, что в арифметической прогрессии шестой член равен –0,6. Чему равна сумма пятого и седьмого ее членов? Сумму каких членов прогрессии можно еще найти? (Приведите пример.)
№ 4. Арифметическая прогрессия задана формулой n-го члена: an = –32 + 4n. Чему равен первый член прогрессии? Какое значение принимает ее разность? Найдите сумму девятого и одиннадцатого ее членов.
№ 5. Между числами –10, 6 и 2 запишите 5 чисел так, чтобы полученные семь чисел образовали арифметическую прогрессию.
Задания Web-квеста
Выполните следующие задания тематического образовательного Web-квеста.
|
<Узнать> |
<Создать> |
<Оформить> |
|
|
Архивы |
– зачем могли понадобиться людям числовые последовательности? – когда и как люди научились суммировать простейшие арифметические прогрессии? – кто из учёных математиков внёс вклад в создание и развитие теории рекуррентных последовательностей? |
– хронологию познания человеком сущности и свойств арифметической прогрессии; – галерею учёных-математиков, внёсших свой вклад в развитие теории числовых последовательностей; – библиографию научных трудов, посвящённых числовым последовательностям |
Проект «Исторический экскурс по арифметической прогрессии» (презентация, реферат, доклад) |
|
Теория |
– различные определения понятий, используемых в теории последовательностей; – взаимосвязи изученных понятий темы «Арифметическая прогрессия» друг с другом; – зависимости, отражённые в формулировках утверждений, касающихся свойств арифметической прогрессии |
– тезаурус темы «Арифметическая прогрессия»; – опорный конспект темы «Арифметическая прогрессия»; – структурно-логическую схему системы понятий темы «Арифметическая прогрессия» |
Проект «Анализ развития теории арифметических прогрессий» (презентация, реферат, доклад). |
|
Приложения |
– встречается ли человек в быту (в повседневной жизни) с числовыми последовательностями? – в каких сферах производственной деятельности вероятнее всего человеку приходится встречаться с арифметической прогрессией? – в каких науках учёные непременно будут иметь дело с арифметической прогрессией? |
– карту приложений арифметической прогрессии; – подборку прикладных задач, решаемых с использованием свойств арифметических прогрессий (технической направленности); – подборку прикладных задач, решаемых с использованием свойств арифметических прогрессий (общекультурного назначения) |
Проект «Применение свойств арифметической прогрессии» (презентация, реферат, доклад) |
|
Проблемы |
– какие свойства арифметической прогрессии применяются при решении арифметических задач? – какие свойства арифметической прогрессии применяются при решении геометрических задач? – какие свойства арифметической прогрессии применяются при решении нестандартных задач по математике? |
– презентацию «Сопоставление скоростей роста арифметических прогрессий»; – анимационную презентацию «Разности площадей вписанных друг в друга многоугольников»; – памятку «Что нужно знать для решения задач с использованием свойств арифметической прогрессии» |
Проект «Исследование использования свойств арифметических прогрессий в нестандартных ситуациях» (исследовательская работа, презентация, доклад) |
|
Ошибки |
– распространённые ошибки, допускаемые при решении задач с последовательностями; – заблуждения (недоразумения), связанные с арифметическими прогрессиями; – математические софизмы, связанные с арифметической прогрессией |
– банк математических ошибок по теме «Арифметическая прогрессия»; – памятку «Так нельзя применять свойства арифметической прогрессии при решении математических задач»; – плакат-предостережение «Осторожно, ошибка!» |
Проект «Ошибки и софизмы по свойствам арифметической прогрессии» (творческая работа, презентация, доклад) |
За необходимой помощью в выполнении заданий Web-квеста обращайтесь в ресурсный центр, расположенный на методическом сайте: http://matematikum.ucoz.ru.
Использование современных Web-квест задачных технологий предоставляет возможность организовать занятия практикума различными способами: выполнение заданий Web-квеста по каждой теме может быть осуществлено в малых группах или индивидуально; в аудитории под руководством педагога или самостоятельно в домашней работе; оформление проектов по итогам выполнения каждого задания также предполагает различные варианты – в печатной, рукописной форме (реферат, исследование, творческая работа) или в виде компьютерного файла, презентации и т.п.; решение задач обобщенных окрестностей, чаще всего, осуществляется на занятии индивидуально каждым студентом либо во фронтальной форме, либо в групповой; при этом в качестве домашнего задания студентам часто предлагается дополнить окрестности (основываясь на различных направлениях обобщения математических задач) и решить подобранные или самостоятельно составленные задачи (один из видов творческой работы).
Таким образом, использование рассмотренного в пособии подхода к построению занятий практикума по решению математических задач в практике обучения позволит не только повысить уровень сформированности профессиональной компетентности учителей математики (в частности, информационной и коммуникационной), готовности их к самообразованию и самостоятельному решению проблем, но и разнообразить формы проведения занятий, что в целом способствует совершенствованию образовательного процесса как в высшей профессиональной школе, так и в дальнейшей практической работе учителей математики.
Статья подготовлена по проекту no. 2954 «Видовое многообразие задачных конструкций продуктивного обучения математике» в рамках базовой части государственного задания Минобрнауки России.
Рецензенты:
Фролов И.В., д.п.н., профессор, заведующий кафедрой физико-математического образования Арзамасского филиала ННГУ, г. Арзамас;
Вострокнутов И.Е., д.п.н., профессор кафедры физико-математического образования Арзамасского филиала ННГУ, г. Арзамас.
Работа поступила в редакцию 28.01.2015