Формирование приоритетных направлений повышения эффективности функционирования растениеводческого подкомплекса АПК связано с двумя основными аспектами: проблемой выбора конкурентных преимуществ и проблемой распределения производственных ресурсов [3], в рамках которых происходит назначение каждому элементу экономической системы определенных видов и объемов конкретных ресурсов. Необходимость решения этих проблем объясняется тем, что любому субъекту экономики для выполнения поставленных перед ней целей требуются различного рода ресурсы, которые ограничены в своих размерах.
Процесс выращивания и переработки растениеводческой продукции требует особых условий транспортировки, переработки, хранения и накопления. Длительное хранение сельскохозяйственной продукции недопустимо, так как его показатели качества существенным образом изменяются (ухудшаются) во времени. Выбор множества поставщиков и распределение количества поставляемого ресурса перерабатывающим предприятиям необходимо решать ежедневно в процессе оперативного планирования и ситуационного управления предприятием [2].
Нестабильность цен на рынке продовольственных товаров и наличие вероятности невыполнения со стороны отдельных поставщиков актов, регламентирующих поставку сырья, приводят к необходимости моделировать сценарии поставки ресурса на предприятие, учитывающие индивидуальные особенности конкретного поставщика и все возможные ситуации, которые могут возникнуть при взаимодействии производителя сельскохозяйственной продукции и перерабатывающих предприятий.
Вариативность во времени структуры поставщиков, параметров сырья и поведения хозяйствующих субъектов делает многие традиционные методы выбора и распределения ресурсов неприменимыми, а неполнота и неопределенность исходной информации и критериев качества значительно осложняет процесс принятия решения и управления.
Правила принятия решений в условиях неопределенности, конфликтности и вызванного ими риска базируются на различных концепциях. Наиболее известной, достаточно исследованной и широко используемой в теории и на практике является концепция теории игр.
Теория игры – это раздел современной математики, в котором изучаются математические модели принятия решений в условиях неопределенности, конфликтности, т.е. в ситуациях, когда интересы сторон (игроков) или противоположные (в случае антагонистических игр), или не совпадают, хотя и не противоположны (в случае игр с непротивоположными интересами) [4]. Основателями теории игры являются американские ученые Джон (Януш) фон Нейман (1903–1957), венгерского происхождения, и Оскар Моргенштерн (1902–1977), австрийского происхождения, которые во второй половине 40-х годов попытались с помощью математики описать характерные для рыночной экономики явления конкуренции как некоторую «игру».
Игра – это формализованное описание (модель) конфликтной ситуации, включающей четко определенные правила действий ее участников, которые пытаются получить определенную победу путем выбора конкретной (в определенном смысле – лучшей) стратегии поведения. Субъект принятия решения (предприятие, хозяйство) называется игроком, а целевая функция – платежной функцией [4]. В игре могут принимать участие несколько игроков, причем некоторые из них могут вступать между собой в постоянные или временные коалиции (союза). В случае образования коалиции игра носит название «коалиционного». Игра двух лиц называется парной игрою. Каждый игрок принимает такие решения, то есть выбирает такую стратегию поведения, чтобы максимизировать свой выигрыш (прибыль) или минимизировать проигрыш (затраты). При этом он не знает, каких стратегий придерживаются другие игроки. Итак, каждый игрок принимает свои решения в условиях неопределенности, а результат выбранной им стратегии зависит от поведения всех участников игры.
Для оптимизации функционирования растениеводческого подкомплекса АПК нами предлагается использовать теорию игр. Предлагаемая базовая модель основывается на предположении, что хозяйства стремятся так повысить уровень использования конкурентных преимуществ и тем самым повысить эффективность растениеводческого подкомплекса АПК, чтобы внешние и внутренние угрозы в результате активизации инновационной деятельности и затраты на мероприятия по стабилизации и сбалансированному развитию экономики принимали минимальное значение. Процесс взаимодействия в этом случае моделируется некоторой итеративной процедурой входа в состояние равновесия по Нэшу специальной игры m мероприятий.
Рассмотрим список из m мероприятий, эффективность которых в каждый момент времени t = 1, 2, … характеризуется переменными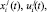 
где i – номер хозяйства (i = 1…n), а j – номер показателя. Заметим, что 
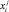– затраты на мероприятия по стабилизации и сбалансированному развитию экономики, а 
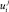– значения корректировок скорости их изменения, необходимые для выбора приоритетных мероприятий.
Гомеостатические состояния группы. Предположим, что на изменение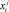 
j экономического показателя i хозяйства растениеводческого подкомплекса АПК оказывают влияние три фактора:
– ее текущее отклонение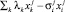 
от базовых параметров экономической эффективности, где lk – это доли участников типа k в списке приоритетных мероприятий, а 
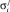«значимость» j экономического показателя i хозяйства растениеводческого подкомплекса;
– ее текущее отклонение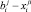 
от внутреннего стандарта bi;
– ее текущее отклонение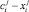 
от внешнего стандарта ci.
В результате этих влияний за время Dt = 1 возникает изменение:
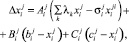(1)
где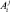 
– коэффициент подражания группе; 
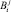– коэффициент «самостоятельности» (инерционности); 
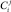– коэффициент склонности к внешнему влиянию. Между j экономическими показателями i хозяйства растениеводческого подкомплекса должны выполняться определенные соотношения связи [83], например такие:
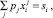(2)
поэтому каждый j показатель (при известных ему, фиксированных собственных значениях переменных других показателей) вынужден добавлять корректировки изменений –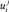 
. Гомеостатическое значение показателя означает, что изменение 
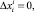т.е.
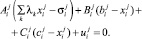(3)
Соотношения (2)–(3) могут выполняться при различных наборах переменных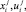 
поскольку число уравнений меньше числа неизвестных, т.е. mn + n < 2mn. Неоднозначность устраняется выбором таких значений переменных 
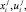которые не только уравновешивают все действующие на i хозяйства показатели экономической эффективности при соблюдении ограничения (2), но и минимизируют затраты на мероприятия по обеспечению конкурентоспособности, стабилизации и сбалансированному развитию растениеводческого подкомплекса:
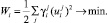(4)
Согласно (4), общие усилия представляют собой сумму (с некоторыми коэффициентами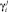 
) квадратов корректировок скоростей изменения, поэтому функционал Wi имеет вполне определенное сходство с кинетической энергией. Множество значени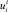й 
и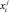 
, из которого выбираются гомеостатические значения, минимизирующие Wi, зависит от реализуемых мероприятий по стабилизации и сбалансированному развитию растениеводческого подкомплекса и мероприятий по устранению внешних и внутренних угроз и неэффективных мероприятий.
В соотношении (3) разность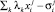 
допускает различную интерпретацию. Если 
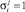, то суммирование идет по всем k ≠ i, и мы имеем простое отличие показателя i от базовых параметров. Если влияние типа k на показатель i оказывается нулевым, или даже «антивлиянием», вызывающим противоположную тенденцию, то этот факт может быть отражен соответствующим увеличением или уменьшением коэффициентов lk, которые в принципе могут быть разными для разных хозяйства растениеводческого подкомплекса АПК.
Объединение (по i) соотношений (2)–(4) в систему уравнений показывает, что такую модель можно представить, как бескоалиционную игру m мероприятий, в которой функции полезности мероприятий зависят только от мероприятий по стабилизации и сбалансированному развитию растениеводческого подкомплекса, в то время как множество допустимых стратегий зависит от мероприятий по устранению и предупреждению внешних и внутренних угроз и неэффективных мероприятий.
В силу этой взаимной зависимости не каждая совокупность наборов
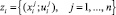(5)
образует эффективность мероприятий группы, а лишь такая, которая одновременно удовлетворяет всем соотношениям (2)–(3). Множество значений таких переменных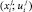 
в пространстве размерности 2mn обозначим:
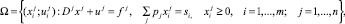(6)
где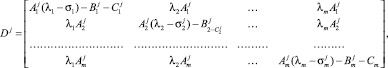 
а xj, uj – векторы размерности m с компонентами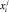 
, у которых индекс i пробегает значения 1, …, m. Заметим, что xi, xj (как и u – переменные) – векторы разного содержания. Нижний индекс (i) означает номер хозяйства, верхний (j) – номер показателя или корректировки. Поэтому вектор xi состоит из всех хозяйств i, а вектор xj содержит показатели j всех исследуемых хозяйств.
Запишем уравнение (3) в явном виде:
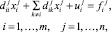(7)
где 
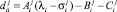и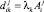 
– элементы матрицы Dj, а 
.
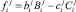Набор z = {z1, …, zm) назовем ситуацией в системе конкурентоспособности. Через z)i( (обозначим часть ситуации z, которая представляет собой набор стратегий всех исследуемых хозяйств, кроме стратегии хозяйства i, т.е.
z)i( = {z1, …, zi–1, zi+1, …, zm} = {zk, k ≠ i}.
Представим нашу игру Г в виде обобщенной игры m мероприятий в смысле Дебре [5]
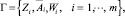(8)
где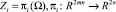 
– проекция пространства R2mn в пространство 
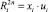, которое состоит из пар n-мерных векторов 
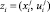. Пусть 
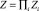, так что не все точки множества Z будут допустимыми: 
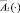– многозначное отображение, ставящее в соответствие каждому набору z)i( множество значений, принадлежащих пространству Zi:
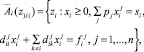(9)
где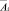 
называется ограничительным отображением хозяйства i. Оно меняет область стратегий этого субъекта в зависимости от ситуации в экономической системе.
Заметим, что множество
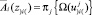(10)
является проекцией некоторого сечения множества W, которое получается, если зафиксировать корректировки всех остальных мероприятий. При этом их показатели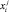 
автоматически определяются согласно (8) при условии
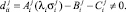(11)
Наконец, каждое хозяйство i на своем множестве стратегий Zi имеет функцию выигрыша Wi:Ui → R1, которая квадратично зависит от его корректировок и имеет вид
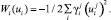(12)
Предполагается, что в ситуации z ∈ Z поведение хозяйства i в обобщенной игре Г взаимодействия m мероприятий состоит в максимизации своей функции выигрыша Wi по отношению к ограничению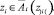 
Таким образом, доказано существование игрового равновесия. Выявлено, что при наличии связей между показателями эффективности устойчивые состояния могут возникать в процессе выбора приоритетных мероприятий по устранению рисков, минимизации затрат и сбалансированному развитию растениеводческого подкомплекса АПК.
Рецензенты:
Балкизов М.Х., д.э.н., профессор, зав. кафедрой «Управление качеством и недвижимостью», ФГБОУ ВПО «Кабардино-Балкарский государственный аграрный университет им. В.М. Кокова», г. Нальчик;
Жерукова А.Б., д.э.н., профессор кафедры «Экономика и менеджмент», АНО ВПО «Белгородский университет кооперации, экономики и права» Нальчикский институт кооперации (филиал), г. Нальчик.
Работа поступила в редакцию 28.01.2015