В контексте данной работы под имитационным моделированием будем понимать метод исследования, при котором реальный механизм с достаточно высокой степенью точности подменяется системой сосредоточенных масс, соединённых между собой кинематическими, упруго-диссипативными, в общем случае нелинейными и допускающими разрывы связями – динамической моделью и её математическим описанием (математической моделью). Экспериментальное исследование на основе таких моделей (численный эксперимент), даёт возможность сделать выводы о степени надёжности, работоспособности механизма при заданных режимах его эксплуатации, а также определить оптимальные параметры этих режимов. Движение конечной системы масс, на которую наложены идеальные, стационарные, голономные связи, может быть описано системами нелинейных дифференциальных уравнений второго порядка – математическая модель. Для составления таких систем часто используют особую форму уравнения Лагранжа второго рода с «лишними» координатами [1, 4].
Для реализации численного решения исходные дифференциальные уравнения (математическая модель) аппроксимируются конечно-разностными схемами (например, метод Рунге-Кутта) – численная реализация математической модели, процесс вычисления которых программируется и осуществляется с помощью компьютера – компьютерная модель.
Таким образом, исследование динамики механической системы представляет собой:
- построение цепочки последовательных приближений: реальный механизм – динамическая модель – математическая модель – численная реализация математической модели – компьютерная модель;
- разработка метода количественного и качественного определения уровня динамических процессов, протекающих в механизме и влияющих на его надёжность и работоспособность под воздействием внешних факторов (скорость работы, технологические усилия) и изменении внутренних параметров (износ кинематических пар, конструкционные нагрузки, параметры регулировки).
Описанная выше методика динамического анализа механизмов известна [1, 4]. Однако, несмотря на постоянное совершенствование, связанное с увеличением числа масс (сложности) моделей, учётом зазоров в кинематических связях, уточнением характеристик упругих связей, параметров диссипации, сил трения, внешних нагрузок, широкого распространения на практике она не получила. Основные причины этого следующие:
- низкая степень точности и большая трудоёмкость расчёта параметров модели, в первую очередь, упруго-инерционных характеристик;
- большая трудоёмкость работ, связанных с разработкой динамической модели конкретного механизма, её математического описания и программной реализации;
- невозможность оценки достоверности полученных результатов без проведения экспериментальных исследований уже готового механизма.
Методика анализа динамических процессов в механизмах разработана автором с целью снижения трудоёмкости динамических исследований механизмов и повышения их достоверности. В её основе лежат методы компонентного моделирования и объектно ориентированных технологий [2, 5, 8], а также методы твердотельного моделирования [3, 4]. Практической реализацией методики является комплекс программ, объединённых в единую систему dam (динамический анализ механизмов) [5–7], позволяющий автоматизировать процесс построения имитационной модели механизма и выполнить его динамический анализ.
Будем рассматривать любой механизм как совокупность некоторых элементов, соединённых между собой различного рода связями. Элемент – это отдельно взятая деталь механизма, какой-то её фрагмент или, наоборот, сразу несколько деталей. Такое определение элемента соответствует понятию объект, – одному из базовых в теории компонентного моделирования сложных динамических систем и объектно ориентированных технологий [2, 5, 8].
Сопоставим каждый элемент какого-либо механизма, например, переноса холодноштамповочного автомата (ХША) АВ1818 (рис. 1), с объектом, согласно данному выше определению. Любые процессы в таком объекте, могут моделироваться каким угодно образом и, в соответствии с принципами инкапсуляции и полиморфизма, на данном этапе их природа и описание, математическое, программное или физическое, не рассматривается.
Такой подход представляет интерес как при решении задач, связанных с разработкой динамических и математических моделей механизмов [1, 4], так и, что особенно существенно, их программных реализаций при дальнейшей компьютерной обработке [6, 7].

Рис. 1. Механизм переноса холодноштамповочного автомата (твердотельная модель и кинематическая схема): 0 – блок кулачков, 1, 2, 3 – рычаги прямого и обратного хода, 4 – зубчатая передача, 5 – кривошип, 6 – тяга и 7 –каретка переноса
Представим реальный механизм в виде соединённых между собой объектов. С каждым объектом свяжем пять наборов характеристик:
- Свойства: массы, моменты инерции, жёсткости, коэффициенты диссипации, параметры передаточных функций и другие, определяющие объект как замкнутую систему.
- Отклики на возмущения со стороны других объектов.
- Силовые возмущения со стороны других объектов.
- Входные параметры, среди которых могут быть кинематические и силовые.
- Выходные параметры (кинематические, силовые и значения критериев оценки различного рода процессов, протекающих в объекте).
Свойства и отклики (пункты 1 и 2) – это величины, целиком зависящие от объекта. Причём первые – постоянные, не зависящие от внешних условий, вторые – зависимые от той среды, в которую помещён объект. Силовые возмущения и входные параметры (пункты 3 и 4) – окружающая объект среда. Выходные параметры (пункт 5) – это набор результирующих данных, позволяющих оценить процессы, протекающие в объекте, после размещения его в конкретной среде. Следует особо отметить, что набор объектов, представляющих механизм (объектное представление) и сам механизм полностью адекватны друг другу. Подмена реальности моделью осуществляется только на уровне объекта. То есть точность результатов динамических исследований определяется исключительно «доброкачественностью» тех объектов, которые в этих исследованиях используются.
Ещё одно уточнение: объект и модель объекта, как следует из вышеизложенного, – понятия различные. Однако при изложении дальнейшего материала термином «объект» будем обозначать его модель.
Объект, моделирующий механическую систему, которая приводится в движение через одно единственное входное звено и имеющий только одно выходное звено, изображён на рис. 2. Ему может соответствовать одна какая-либо деталь (или её фрагмент) достаточно сложного механизма, например, нижнее плечо рычага прямого хода системы переноса ХША АВ1818 (рис. 1, поз. 1). Входной параметр в данном случае – угол поворота кулачка φ0, выходной – угол поворота рычага φ1. В то же время это может быть и более сложная механическая система – кулачковый механизм привода системы переноса (поз. 0, 1, 2), весь привод (детали, обозначенные на рис. 1 позициями с 0 по 7), или даже вся система переноса целиком.
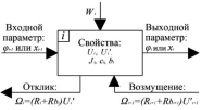
Рис. 2. Объект, моделирующий механическую систему с одним входным и одним выходным звеном
Входными параметрами объекта являются функция перемещения (углового или линейного) предшествующего ему объекта φ1 – 1 и внешние нагрузки Wi на этот объект (например, силы и моменты сил трения, конструкционные и технологические).
Выходной параметр соответственно – функция перемещения выходного звена. Свойства – набор констант, определяющих количественные характеристики модели, соответствующей данному объекту. Среди них, параметры функций положения и передаточных функций (для входного звена это Ui и 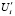 ), упруго-инерционные и диссипативные характеристики. Отклик, по существу выходной параметр, – воздействие сил упругости Ri и диссипации Rbi в первом фрагменте входного звена, на объект предшествующий. Возмущение – это отклик со стороны следующего объекта (или следующих, если их несколько) на данный объект.
), упруго-инерционные и диссипативные характеристики. Отклик, по существу выходной параметр, – воздействие сил упругости Ri и диссипации Rbi в первом фрагменте входного звена, на объект предшествующий. Возмущение – это отклик со стороны следующего объекта (или следующих, если их несколько) на данный объект.
 а)
а) 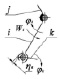 б)
б) 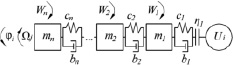 в)
в)
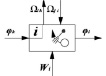
Рис. 3. Объект – вращающийся рычаг: а – обозначение на объектном представлении механизма, б – кинематическая схема, в – динамическая модель
Конкретным примером объекта, представленного на рис. 2, является, в частности, объект, именуемый в дальнейшем рычаг или качающийся рычаг (рис. 3), движение которого описывается n-массовой динамической моделью и соответственно системой n-нелинейных дифференциальных уравнений второго порядка. Компьютерной (программной) реализацией этого объекта будет итерационная схема решения системы уравнений, полученная с помощью одного из многочисленных методов их численного интегрирования.
При построении объектной модели механизма и соответственно математической и программной её реализации в общем случае приходится решать следующие задачи:
- Разработка, если это необходимо, новых объектов и добавление их к базе объектов уже, существующих.
- Подготовка данных о свойствах объектов.
- Выбор из базы существующих объектов тех, которые необходимы для построения объектно ориентированного представления механизма, и создание этого представления.
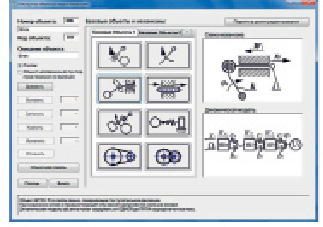
Рис. 4. Конструктор объектной модели
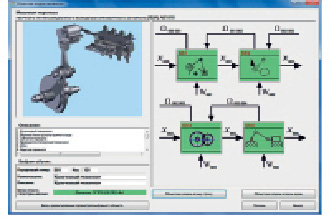
Рис. 5. Объектная модель
Построение объектно ориентированной модели из уже готовых объектов осуществляется путём их последовательного соединения в одну схему. В системе dam работа по созданию объектной модели осуществляется в интерактивном режиме (рис. 4, 5). На данном этапе параллельно с объектным представлением автоматического механизма создаётся и его математическая модель [5].
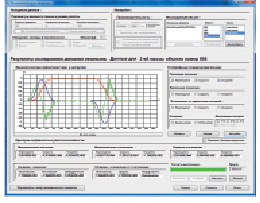
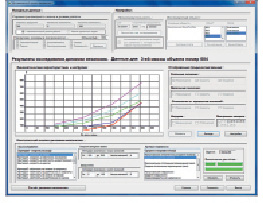
На рис. 6 показано основное окно определения параметров имитационного моделирования механизмов и вывода результатов расчётов. Здесь определяется исследуемый объект, на рис. 6 кривошипно-ползунный механизм перемещения каретки переноса, скорость работы механизма, режим его работы (одиночных ходов или автоматический), начальное и конечное положение входного звена. Значения данных объектов: количество масс, кинематические, упруго-инерционные и диссипативные характеристики, нагрузки, параметры зазоров и погрешности изготовления назначаются при разработке объектной модели механизма. Однако, что является несомненным достоинством системы dam, некоторые из этих данных (зазоры, погрешности изготовления, силы диссипации, трения, конструкционные нагрузки и технологические усилия) могут быть исключены из процесса моделирования.
 a)
a)
 б)
б)
Рис. 6. Исследования динамики механизма в системе dam: а – расчёт динамических характеристик, б – анализ работоспособности механизма в зависимости от скорости его работы и степени износа кинематических пар
При построении стратегий имитационного моделирования имеется возможность изменить значения большинства параметров объектов. Оценка работоспособности исследуемого механизма может быть выполнена на основании двух категорий показателей, определяющих уровень и характер динамических процессов, протекающих при имитации работы механизма при заданных условиях: графического отображения данных и расчётных значений ряда критериев (рис. 6, а).
Процесс построения схем исследования надёжности и работоспособности механизма может быть автоматизирован путём использования уже готовых решений. При реализации каждого из них имеется возможность оценить работоспособность механизма по десяти критериям.
Результат применения одной из таких схем: построение функции изменения среднего значения величины ускорения каретки переноса в зависимости от скорости работы механизма и величины зазоров (степени износа) в кинематических парах – показан на рис. 6, б.
Предложенная в работе методика имитации динамических процессов, протекающих в механических системах (механизмах), позволяет решить следующие задачи:
- Автоматизировать процесс создания компьютерных моделей механизмов, имитирующих их работу при различных условиях эксплуатации и различных вариантах конструкционных исполнений деталей, их соединений и точности изготовления.
- Обеспечить на этапе построения объектной модели механической системы и её компьютерной реализации требуемую адекватность реальному механизму и соответственно точность решаемых на её основе задач.
- Выполнить на этапе проектирования механизма оценку его надёжности и работоспособности на основе данных, характеризующих уровень динамических процессов в его элементах, и определить пути оптимизации конструкции и режимов эксплуатации механизма.
Рецензенты:
Корнеев А.М., д.т.н., директор института машиностроения, Липецкий государственный технический университет, г. Липецк;
Лебедев С.В., д.т.н., профессор, заведующий кафедрой технологий сварки и покрытий Липецкого государственного технического университета, г. Липецк.
Работа поступила в редакцию 29.12.2014.



