В последнее время все большее внимание уделяется изучению процессов естественной конвекции [4]. Исследование конвективного теплопереноса позволяет проводить выбор оптимальных режимов работы в любой области и соответствующих технических решений. Но при моделировании конвективных течений в областях больших размеров достаточно часто приходится учитывать турбулентность [5]. Одним из важных вопросов при решении задачи движения воздуха или жидкости является модель турбулентности [3]. В монографии Шлихтинга Г. [6] говорится об обоснованности применения полуэмпирических формул для расчета свободной турбулентности (турбулентные течения без ограничивающих стенок) [10]. Поэтому вопрос о возможных вариантах моделей конвективного теплопереноса в замкнутых объемах при локальном нагреве весьма актуален.
Цель работы – анализ двух различных подходов к моделированию свободно-конвективного теплопереноса в режиме турбулентной конвекции (модели Прандтля и Прандтля-Райхарда).
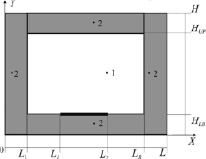
Рис. 1. Область решения задачи: 1 – воздух; 2 – ограждающие конструкции; L, Н – длина и ширина области решения; Индексы: L, R, UP, LB – левая, правая, верхняя и нижняя границы раздела сред
Постановка задачи
Для физической постановки задачи выбрана достаточно простая по геометрии замкнутая прямоугольная область, включающая воздух (1) и ограждающие конструкции (2). На трех внешних границах приняты условия теплоизоляции, на левой внешней границе X = 0 реализованы условия теплообмена с окружающей средой. По всему периметру границы раздела сред заданы граничные условия четвертого рода (равенство тепловых потоков и температур) за исключением участка на нижней границе, где находится источник тепловыделения (L1 < X < L2).
Математическая постановка задачи
Численное моделирование естественной конвекции в замкнутой области с учетом турбулентности проведено двумя способами. Постановка задачи включала систему дифференциальных уравнений Навье-Стокса для газа и теплопроводности для твердых стенок. Турбулентная составляющая учитывалась реализацией алгебраических моделей Прандтля-Райхарда и Прандтля [1]. Моделирование было проведено в системе MathLab.
Математическая постановка принималась аналогичной [7, 9] и имела вид:
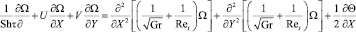 , (1)
, (1)
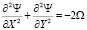 , (2)
, (2)
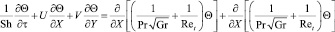 , (3)
, (3)
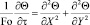 . (4)
. (4)
Начальные условия для системы уравнений (1–4)
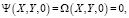
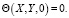 (5)
(5)
Граничные условия на трех внешних границах области решения
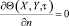 . (6)
. (6)
На левой внешней границе
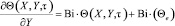 . (7)
. (7)
На границах раздела ограждающих конструкций и газа, выполняются условия:
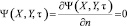 ,
, 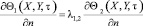 , (8)
, (8)
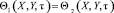 .
.
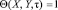 ,
, 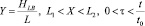 , (9)
, (9)
где X, Y – безразмерные декартовы координаты; Θ – безразмерная температура; Ω – безразмерный аналог вихря скорости; 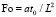 – число Фурье; Gr = gβL3(Tit – T0)v2 – число Грасгофа; g – ускорение, создаваемое массовыми силами, м/с2; а – коэффициент температуропроводности, м2/с; β – температурный коэффициент объемного расширения, К-1; Bi = αL/λ – число Био; α – коэффициент теплоотдачи между внешней средой и рассматриваемой областью решения, Вт/(м2∙К); Re = U∙L/vt – число Рейнольдса; Pr = v/a – число Прандтля; T – температура, К; T0 – температура в начальный момент времени, К; Tit – масштаб температуры, К; V0 – масштаб скорости (скорость конвекции), м2/с; U, V – безразмерные скорости; t – время, с; t0 – масштаб времени, с; λ – коэффициент теплопроводности твердой стенки, Вт/(м⋅К); λ1,2 – относительный коэффициент теплопроводности; νt – коэффициент турбулентной кинематической вязкости, м2/с; τ – безразмерное время; ψ – безразмерный аналог функции тока.
– число Фурье; Gr = gβL3(Tit – T0)v2 – число Грасгофа; g – ускорение, создаваемое массовыми силами, м/с2; а – коэффициент температуропроводности, м2/с; β – температурный коэффициент объемного расширения, К-1; Bi = αL/λ – число Био; α – коэффициент теплоотдачи между внешней средой и рассматриваемой областью решения, Вт/(м2∙К); Re = U∙L/vt – число Рейнольдса; Pr = v/a – число Прандтля; T – температура, К; T0 – температура в начальный момент времени, К; Tit – масштаб температуры, К; V0 – масштаб скорости (скорость конвекции), м2/с; U, V – безразмерные скорости; t – время, с; t0 – масштаб времени, с; λ – коэффициент теплопроводности твердой стенки, Вт/(м⋅К); λ1,2 – относительный коэффициент теплопроводности; νt – коэффициент турбулентной кинематической вязкости, м2/с; τ – безразмерное время; ψ – безразмерный аналог функции тока.
Уравнения (1–4) с соответствующими начальными и граничными условиями (5–9) решены методом конечных разностей на равномерной сетке. При решении задачи (1) – (9) использовался алгоритм [7–9], разработанный для численного решения задач естественной конвекции в замкнутых прямоугольных областях с локальными источниками энергии. Турбулизация течения нагретого воздуха описывалась в соответствии с основными положениями [1]: изменением вязкости с ростом скорости движения воздуха. Расчет вязкости проведен в рамках модели Прандтля-Райхарда [1]:
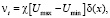
где Umax и Umin – максимальная и минимальная величины скорости в слое, δ – полуширина слоя смешения, Χ – эмпирический безразмерный параметр, постоянный по толщине слоя, х – расстояние, измеренное в направлении потока.
Модели Прандтля [1] соответствует определение коэффициента турбулентной вязкости по формуле:
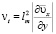 ,
, 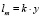 ,
,
где lm – путь смешения, x, y – координаты, м; υ – компонента скорости, м/с; k – универсальный коэффициент пропорциональности, не зависящий от числа Рейнольдса.
Результаты исследования и их обсуждение
Результаты математического моделирования свободно-конвективных течений в замкнутой области при наличии источника тепловыделения представлены на рис. 2–4.
Численные исследования проведены при значениях температур: начальной – Θ0 = 0, источника тепловыделения – Θit = 1, окружающей среды – Θe = 0.
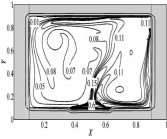
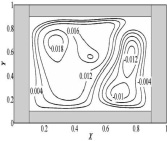
а) б)
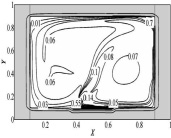
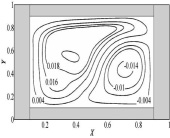
в) г)
Рис. 2. Поля температур (a, в) и изолинии функции тока (б, г) при τ = 500 для модели Прандтля-Райхарда (а, б) и модели Прандтля (в, г)
При математическом описании исследуемого процесса контролировались условия геометрического подобия реальных систем. В результате численного решения задачи получены распределения температур для исследуемой области и изолинии функции тока, характеризующие основные закономерности процесса теплопереноса (рис. 2–3).
При малых временах, например (τ= 50), теплоотвод с левой внешней границы еще не оказывает заметного воздействия и в воздушной области формируется симметричное температурное поле. Распределение температуры (рис. 2) наглядно иллюстрирует влияние подъемной силы, которая обусловлена неоднородностью поля температур. Анализ средних по газовой области температур позволяет говорить об их существенно неравномерном распределении во времени из-за влияния архимедовой силы (таблица).
На рис. 4–5 приведено изменение среднего числа Нуссельта по вертикальным (X = LL, X = LR) границам раздела сред во времени, определенного по выражениям [9]:
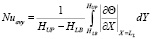 ;
;
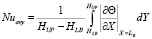 .
.
При увеличении временного параметра становится заметным вихреобразование. Основной поток нагретого воздуха смещается к правой границе раздела сред, в верхней части которой происходит интенсивный теплообмен между нагретым газом и холодной ограждающей конструкцией. Следствием этого является (рис. 4) увеличение среднего числа Нуссельта на границе X = LR.
Температурные поля, полученные при реализации двух разных подходов к моделированию турбулентности достаточно сопоставимы, направления движения нагретого воздуха совпадают.
Зависимость средней температуры воздуха от времени: 1 – модель Прандтля-Райхарда, 2 – модель Прандтля
|
t, c |
50 |
100 |
150 |
200 |
250 |
300 |
400 |
450 |
500 |
|
модель Прандтля-Райхарда |
278,7 |
278,8 |
278,57 |
278,52 |
278,66 |
279,5 |
279,19 |
279,17 |
278,51 |
|
модель Прандтля |
277,33 |
278,53 |
276,91 |
276,89 |
276,9 |
277,23 |
277,44 |
277,6 |
277,64 |
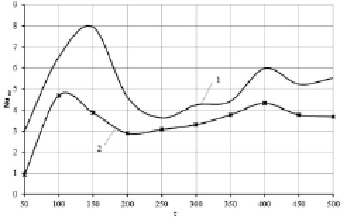
Рис. 3. Зависимость среднего числа Нуссельта от времени для границы X = LL: 1 – модель Прандтля-Райхарда, 2 – модель Прандтля
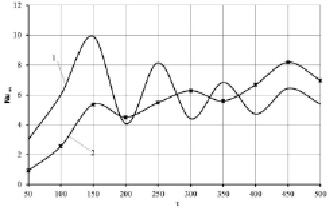
Рис. 4. Зависимость среднего числа Нуссельта от времени для границы X = LR: 1 – модель Прандтля-Райхарда, 2 – модель Прандтля
Можно отметить, что полученные результаты иллюстрируют стабилизацию режимов теплообмена на границах раздела «воздух – твердая стенка» при относительно больших временах (t = 500), за исключением правой границы раздела «воздух – ограждающая конструкция». При этом средние числа Нуссельта с ростом времени растут по мере увеличения t более чем в 2 раза. Результаты численного моделирования показывают возможность применения разных подходов к описанию тепловых режимов турбулентной конвекции в замкнутых областях с локальными источниками тепловыделения.
Заключение
Проведено теоретическое исследование турбулентной естественной конвекции в системе с источником тепловыделения. Полученные результаты позволяют оценить характер течения и интенсивность анализируемого процесса теплопереноса, а также новую информацию, которая не только характеризует конвективный режим течения, но и является дополнительной для построения и апробации белее сложных моделей турбулентности, учитывающих особенности конвективного теплопереноса в больших замкнутых объемах при локальном нагреве. Результаты математического моделирования позволяют сделать выводы о возможности применения алгебраической модели Прандтля для рассмотрения турбулентных течений при естественной конвекции в геометрически простых областях [2]. Применение данной модели целесообразно в случае, когда движение нагреваемого источником тепловыделения воздуха осуществляется за счет подъемной силы [10]. Следует отметить, что применение алгебраической модели при расчете свободно-конвективных течений в турбулентном режиме значительно проще и требует меньшего времени вычислений, чем более сложные модели турбулентности.
Работа выполнена в рамках НИР Госзадания «Наука» (Шифр ФЦП 2.1321.2014).
Рецензенты:
Борисов Б.В., д.ф.-м.н., профессор кафедры «Теоретическая и промышленная теплотехника» НИ ТПУ, г. Томск;
Голдаев С.В., д.ф.-м.н., старший научный сотрудник, профессор кафедры «Теоретическая и промышленная теплотехника» НИ ТПУ, г. Томск.
Работа поступила в редакцию 29.12.2014.



