Процессы теплопереноса в замкнутых областях с локально сосредоточенными источниками нагрева интенсивно исследуются в последние годы (например, [4–7]) теоретически. Экспериментальных данных по основным характеристикам теплопереноса в таких достаточно типичных для многих практических приложений условиях опубликовано мало (достаточно типичны статьи [1, 3]). Кроме того, эксперименты типа [1, 3] проводились на моделях с характерными размерами много меньше аналогичных размеров практически значимых объектов (например, теплоснабжения). Обоснование же теоретических следствий анализа таких процессов необходимо проводить с использованием результатов экспериментов, полученных на моделях, размеры которых максимально приближены к реальным.
Возможны различные варианты расположения источников нагрева на внутренних поверхностях моделей [1, 3–6]. Наименее изучен процесс теплопереноса в прямоугольной замкнутой области с источником лучистого нагрева, расположенным на верхней границе области или вблизи ее. Таким источником, например, может быть газовый инфракрасный излучатель (ГИИ) [2].
Целью работы является экспериментальное изучение температурных полей в заполненном воздухом крупногабаритном объеме с расположенными на его верхней поверхности излучателями.
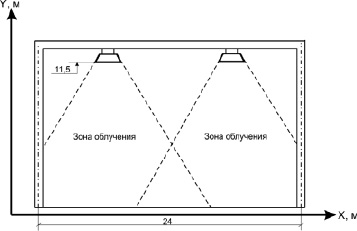
Рис. 1. Схема области проведения экспериментальных исследований
Экспериментальные исследования выполнялись в зимний период времени при температурах наружного воздуха от –5 до –42 °С на крупногабаритных моделях больших характерных размеров (от 11 до 24 м). Исследовались температурные поля, формирующиеся при работе ГИИ, расположенных в верхней части (рис. 1) области регистрации температур. Относительная влажность внутреннего воздуха составляла < 65 %.
Система нагрева включала десять излучателей К 8430 RN, производства фирмы «GoGas» (Германия) тепловой мощностью 30 кВт каждый. Средняя плотность лучистого теплового потока составляла на уровне нижней границы области (рис. 1) ~25 Вт/м2, на высоте ~1,7 м – 100 Вт/м2.
Излучатели располагались параллельно нижней границе на высоте 11,5 м. Измерения температур выполнялись термопарами в характерных сечениях между излучателями на одинаковом расстоянии от них. По результатам измерений установлены распределения температур по координате y. Типичное распределение приведено на рис. 2.
Первичная статистическая обработка результатов экспериментов показала, что выборочное среднее равно t = 19,05 °С при несмещённой оценке среднего квадратического отклонения S = 2,01. Можно сделать вывод о том, что 95 % экспериментальных значений температуры находятся в интервале (15,03–23,07).
Коэффициент корреляции усредненных результатов измерений равен 0,65, что свидетельствует о наличии связи t(y), а зависимость рис. 2 иллюстрирует нелинейность этой связи.
Получено уравнение регрессии. Спецификация по графическому изображению показала, что наилучшей является нелинейная регрессионная модель в виде полинома 4-й степени:
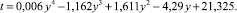
Для вычисления оценок коэффициентов регрессии на первом этапе проводилась линеаризация уравнения с помощью замены: z1 = y; z2 = y2; z3 = y3; z4 = y4, в результате которой была получена линейная модель множественной регрессии вида
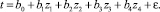
Оценки коэффициентов b0, b1, b2, b3, b4 проведены методом наименьших квадратов для множественной регрессии.
При доказательстве статистической значимости коэффициентов полученного уравнения регрессии определены стандартные ошибки оценок его коэффициентов. Критическое значение распределения Стьюдента установлено по соответствующим таблицам критических точек при уровне значимости 5 %. Сделан вывод, что все коэффициенты полученного уравнения регрессии являются статистически значимыми.
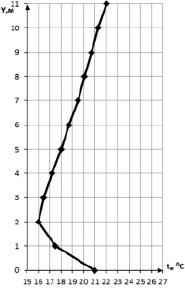
Рис. 2. Распределение температуры воздуха по y в сечении x = 12 между двумя излучателями
О высоком качестве математической модели, полученной по результатам экспериментов, свидетельствует и коэффициент детерминации R2 = 0,989. Его статистическая значимость также установлена при 5 % уровне с применением статистики распределения Фишера.
Ниже приведена таблица опытных значений температуры, вычисленных по формуле регрессии (1). Сумма погрешностей результата незначительно отличается от нуля. Таким образом, установлено, что одно из условий Гаусса – Маркова, которые определяют предпосылки использования метода наименьших квадратов, выполнено.
С помощью теста ранговой корреляции Спирмена было доказано выполнение второго условия Гаусса – Маркова о постоянной дисперсии отклонений εi для любых наблюдений i и j:
D(εi) = D(εj) = σ2.
На основании статистического анализа показано, что выводы, сделанные выше на основе F-статистики, являются надежными.
Полученные результаты экспериментальных исследований являются базой для описания механизма теплопереноса в рассматриваемых типичных для многих практических приложений условиях.
Распределение температур по координате y (рис. 2.) в типичном сечении по x иллюстрирует особенности изучаемого процесса. Теплота, генерируемая газовыми инфракрасными излучателями, поступает к нижней границе области и аккумулируется тонким приповерхностным слоем горизонтальной стенки. Температура поверхности этой стенки растет, и создаются условия для прогрева нижних слоев воздуха, прилегающих к границе y = 0. В результате формируются свободноконвективные течения, за счет которых осуществляется охлаждение нижней стенки и нагрев выше лежащих слоев воздуха. Локальный минимум температур в зоне y ≈ 2 м обусловлен совместным влиянием процессов естественной конвекции и теплопроводности в воздухе. На основании результатов выполненных исследований можно сделать вывод о целесообразности моделирования процессов естественной конвекции и теплопроводности при анализе теплопереноса в замкнутых прямоугольных областях с лучистыми источниками нагрева на верхней границе.
Экспериментальные (tэ) и вычисленные по формуле регрессии (tр) значения температуры
|
y, м |
tэ, °С |
tр |
εi = tэ – tр |
|
0,1 |
21,0 |
20,84699 |
0,153011 |
|
1 |
2 |
3 |
4 |
|
1,0 |
17,58 |
17,75078 |
–0,17078 |
|
2,0 |
16,02 |
16,30932 |
–0,28932 |
|
3,0 |
16,42 |
16,24349 |
0,176508 |
|
4,0 |
17,25 |
16,94095 |
0,309045 |
|
5,0 |
18,07 |
17,93416 |
0,135842 |
|
6,0 |
18,7 |
18,90032 |
–0,20032 |
|
7,0 |
19,4 |
19,66143 |
–0,26143 |
|
8,0 |
20,12 |
20,18425 |
–0,06425 |
|
9,0 |
20,72 |
20,5803 |
0,1397 |
|
10,0 |
21,32 |
21,1059 |
0,214102 |
|
11,0 |
22,02 |
22,16211 |
–0,14211 |
На основании результатов проведенных экспериментальных исследований температурных полей в замкнутой прямоугольной области с источником лучистого нагрева (газовые инфракрасные излучатели) вблизи верхней границы можно сделать вывод о механизме теплопереноса в рассматриваемых достаточно типичных для многих практических приложениях условиях. Теплоперенос в воздухе, заполняющем исследуемый объем, осуществляется за счет совместно протекающих процессов свободной конвекции и теплопроводности.
Работа выполнена в рамках НИР Госзадания «Наука» (Шифр Федеральной целевой программы 2.1321.2014).
Рецензенты:
Заворин А.С., д.т.н., зав. кафедрой парогенераторостроения и парогенераторных установок, НИ ТПУ, г. Томск;
Логинов В.С., д.ф.-м.н., профессор кафедры теоретической и промышленной теплотехники, НИ ТПУ, г. Томск.
Работа поступила в редакцию 28.12.2014.



