Дискретные динамические системы, в частности цифровые фильтры и системы управления, в настоящее время, как правило, реализуются с применением оператора сдвига, связанного с широко известным z-преобразованием. Данный оператор, несмотря на широкое распространение, не всегда хорошо подходит для реализации дискретных систем на вычислительных машинах с ограниченной длиной разрядной сетки. Сопутствующие негативные эффекты особенно ярко выражены при высоких частотах дискретизации системы. Это накладывает ограничения на применение оператора сдвига при моделировании высокочастотных, разноскоростных или жестких динамических систем, делая в некоторых случаях их цифровую реализацию невозможной.
Для решения обозначенной проблемы был введен δ-оператор. Системы на основе δ-оператора малочувствительны к высокой частоте дискретизации, а также обладают рядом других важных свойств. Например, при стремлении периода дискретизации к нулю дискретная система на основе δ-оператора переходит в эквивалентную ей непрерывную [1]. В последние двадцать лет число публикаций по теме δ-оператора устойчиво растет. Краткий обзор научных работ последних лет показывает широкие возможности δ-оператора и его пригодность к применению в различных областях техники [1, 4, 6].
Почему же δ-оператор до сих пор не получил повсеместного распространения? Объективная причина этого лежит в отсутствии четко сформулированных критериев предпочтительности применения δ-оператора в той или иной задаче, поскольку характеристики системы при замене оператора сдвига на δ-оператор улучшаются далеко не всегда. Подавляющее большинство работ посвящено применению δ-оператора в частных случаях; некоторые публикации посвящены авторским модификациям δ-оператора [3, 5]. Однако работ, в которых указывались бы критерии применимости δ-оператора, нами найдено не было. Настоящая статья имеет своей целью устранение данного недостатка.
Определение δ-оператора
Воспользуемся аппроксимацией Эйлера для вычисления производной:
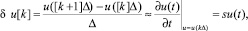(1)
где Δ = T – период дискретизации. Как эквивалент оператора s, введем оператор δ, который имеет следующий смысл:
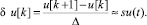(2)
По определению оператора сдвига
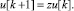(3)
Из (2) и (3) следует связь между операторами δ и z:
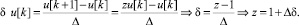(4)
Начальные условия при этом считаются нулевыми.
Описание дискретной динамической системы в пространстве состояний имеет вид
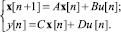(5)
Собственные числа дискретной системы при уменьшении периода дискретизации стремятся к единице [1]. Отсюда следует, что матрица A дискретного пространства состояний стремится к единичной матрице. Так, для системы второго порядка
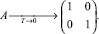(6)
Этот эффект приводит к появлению существенного разброса между близкими к единице диагональными коэффициентами матрицы и недиагональными, близкими к нулю, что вызывает трудности при машинном представлении матрицы A. Ее коэффициенты как бы скапливаются в разных концах разрядной сетки, оставляя середину пустой. В результате происходит заметная потеря точности моделирования. Это справедливо и для арифметики с плавающей запятой, так как экспонента диагональных коэффициентов при малых периодах дискретизации всегда равна единице, а для представления мантиссы используется ограниченное число разрядов.
Эту трудность можно частично разрешить, если применить δ-оператор. В дискретном пространстве состояний система на основе δ-оператора определяется следующим образом:
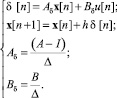(7)
На основании формулы (4) должно выполняться условие Δ = T. Однако это условие не обязательно; Δ можно интерпретировать как дополнительный параметр дискретной системы. С одной стороны, он позволяет масштабировать переменные состояния, с другой – его можно подобрать таким образом, чтобы минимизировать цифровой шум модели [2]. Он также влияет на коэффициенты модели, что особенно важно при создании моделей в арифметике с фиксированной запятой. Обычно полагают, что Δ ∈ (0; 1]. В работах [1, 2] рекомендуется выбирать в качестве Δ число, равное 2m; это упрощает аппаратную реализацию и делает погрешность представления Δ на цифровом вычислителе равной нулю. Кроме того, выбор Δ как степени двойки упрощает задачу оптимизации, которую необходимо решить при выборе значения Δ.
Исследование системы первого порядка
Рассмотрим одномерную систему, описываемую следующим уравнением:
. (8)
Чтобы данная модель была физически реализуема, коэффициент a должен быть вещественным. Пусть T – период дискретизации. Исследуем, при каком значении aT для модели (8) большую точность будет давать обычное z-преобразование, а для каких – δ-преобразование. Применив к (8) линейный оператор билинейного преобразования
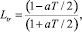(9)
получим дискретную модель
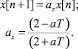(10)
График зависимости az от aT приведен на рис. 1. Это гипербола, левая ветвь которой монотонно убывает. Правее нуля находится область неустойчивости метода трапеций, поэтому рассматривать поведение графика в этой области не имеет смысла.
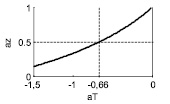
Рис. 1. График зависимости az от aT
Эквивалентная (8) δ-модель такова:
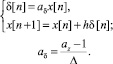
Обратим внимание, что, так как Δ равно степени числа 2, то оно никак не влияет на точность машинного представления aδ. Примем для простоты, что Δ = 1. Хотя погрешность машинного представления az и aδ имеет «пилообразный» вид, по графику на рис. 1 можно достаточно точно описать поведение этой погрешности. Дельта-модель будет иметь в целом меньшую погрешность при
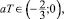(11)
поскольку в этом случае az ближе к 1, а aδ = az – 1, соответственно, ближе к 0, и точка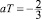 
задает границу областей предпочтительности операторов: 
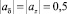. Рис. 2 демонстрирует результаты численного эксперимента над моделью с представлением данных с плавающей запятой при точности представления single (32 бита, мантисса 23 бита), подтверждающие описанный выше характер погрешности. На графиках изображены модули абсолютной погрешност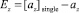и 
и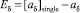 
в логарифмическом масштабе, где [az]single и [aδ]single – машинные представления коэффициентов az и aδ при точности single в сравнении с коэффициентами точности double.
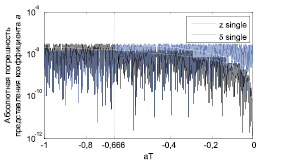
Рис. 2. График погрешностей машинного представления коэффициентов
Вертикальным пунктиром на рис. 2 отмечена линия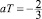 
, белой линией – верхняя оценка погрешности [aδ]single, выполняемая на интервале [–1; 0) по формуле
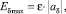(12)
где ε – машинный эпсилон для числа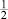 
, то есть значение младшего бита мантиссы [aδ] при неизменном значении экспоненты. Для чисел с фиксированной запятой ε – просто минимальное число на текущей разрядной сетке. В данном случае ε = 5,96∙10–8.
Погрешности Eδ убывают ступенчато, уменьшаясь каждый раз, когда мантисса представления aδ получает дополнительный двоичный разряд по сравнению с представлением az. Это происходит при достижении aδ значений: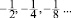 
Верхняя оценка погрешности машинного представления az на интервале [–1; 0) равна
(13)
Формулы (12) и (13) дают простой способ оценить выигрыш в точности представления коэффициентов δ-модели независимо от типа данных и разрядности машинного слова:
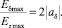(14)
Исследование системы второго порядка
Рассмотрим теперь системы второго порядка с комплексно-сопряженными собственными значениями λ12 = σ ± iω, которые могут быть представлены в форме пространства состояний с действительной матрицей
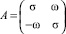. (15)
Матрица A с помощью линейного преобразования переходит в матрицу Az, которой соответствует матрица эквивалентной δ-модели Aδ:
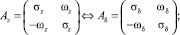
σδ = σz – 1; (16)
ωδ = ωz, (17)
при Δ = 1. Погрешность машинного представления ωδ и ωz одинакова и уменьшается с уменьшением шага дискретизации; соотношения же верхних оценок погрешностей машинного представления σδ и σz те же, что и в предыдущем случае:
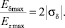
На рис. 3 изображен фрагмент поля комплексных чисел λT = σT + iωT, на который нанесены значения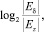 
отражающие количественное превосходство точности машинного представления σδ по сравнению с машинным представлением σz. Область, в которой дельта-оператор демонстрирует не менее высокую точность, чем z-оператор, может быть аппроксимирована частью эллипса с центром в точке 0 и полуосями (0,66; 1,15), лежащей в левой комплексной полуплоскости. Обозначим Pδ – область предпочтительности δ-оператора. Эксперименты показывают, что внутри указанного эллипса коэффициенты системы на основе δ-оператора не менее точны в 97 % случаев (причем 
только на границе Pδ из-за неточности аппроксимации действительной области предпочтительности эллипсом). Однако условие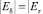 
выполняется в 35 % точек внутри Pδ. Обозначим Rδ – сильная область предпочтительности, где 
в 95 % точек. Для системы второго порядка Rδ может быть аппроксимирована частью эллипса с центром в точке 0 и полуосями (0,09; 0,16). Для системы первого порядка Rδ – отрезок на действительной оси (–0,09; 0).
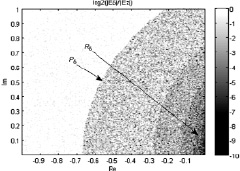
Рис. 3. Машинное представление σδ по сравнению с машинным представлением σz
Критерии предпочтительности δ-оператора
При синтезе дискретной модели исходной непрерывной системы следует руководствоваться следующим. Если λT ∈ Pδ, где λ – собственное число (полюс) системы, T – период дискретизации, Pδ – слабая область предпочтительности δ-оператора, то его применение дает не меньшую точность представления коэффициентов системы, чем применение z-оператора. При использовании билинейного преобразования для синтеза системы в форме пространства состояний слабые области предпочтительности имеют вид:
1. Для системы первого порядка Pδ – отрезок на действительной оси (–0,66; 0).
2. Для системы второго порядка Pδ может быть аппроксимирована с доверительной вероятностью 97 % частью эллипса с центром в точке 0 и полуосями (0,66; 1,15), лежащей в левой комплексной полуплоскости.
Если λT ∈ Rδ, где Rδ – сильная область предпочтительности δ-оператора, то его применение дает большую точность представления коэффициентов системы в 95 % случаев, чем применение z-оператора. При использовании билинейного преобразования для синтеза системы в форме пространства состояний сильные области предпочтительности имеют вид:
1. Для системы первого порядка Rδ – отрезок на действительной оси (–0,09; 0).
2. Для системы второго порядка Rδ может быть аппроксимирована частью эллипса с центром в точке 0 и полуосями (0,09; 0,16).
Заключение
В работе исследуются границы применимости δ-оператора к дискретным линейным динамическим системам в форме пространства состояний при использовании для их синтеза билинейного преобразования. Введены понятия сильной и слабой областей предпочтительности δ-оператора. Сформулирован простой критерий предпочтительности δ-оператора для звеньев первого и второго порядка, основанный на исследовании их полюсов. Данный критерий позволяет оценить, возможно ли повысить точность машинного представления системы при применении δ-оператора. Предметом дальнейшего исследования является формулировка критерия предпочтительности для динамических систем в форме передаточных функций, а также при использовании арифметики с фиксированной запятой.
Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований в рамках договора № НК 14-01-31277\14 от 06.02.2014 г.
Рецензенты:
Авдеев Б.Я., д.т.н., профессор кафедры информационно-измерительных систем и технологий, ФГАОУ ВО «Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» им. В.И. Ульянова (Ленина)», г. Санкт-Петербург;
Анисимов В.И., д.т.н., профессор кафедры систем автоматизированного проектирования. ФГАОУ ВО «Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» им. В.И. Ульянова (Ленина)», г. Санкт-Петербург.
Работа поступила в редакцию 28.12.2014.