Теплоснабжение с помощью тепловых насосов (ТН) относится к области энергосберегающих технологий и находит всё большее применение [1, 3]. При использовании в качестве низкопотенциального источника теплоты промышленных сбросов и коммунальных сточных вод для ТН возникает необходимость анализа тепловых режимов водоемов, в которых располагают теплообменник-испаритель. Исследования значительно усложняются из-за необходимости учета режима смешанной конвекции, возникающей вследствие совместного влияния стока тепла, участков ввода (вывода) жидкости и неоднородного теплоотвода с верхней границы области решения.
В последнее время исследованию функционирования теплонасосных установок уделяется большое внимание, но математические модели, описывающие подобные процессы, встречаются достаточно редко. Отсутствует достоверная информация о воздействии окружающей среды на работу ТН. Во многих же случаях значительную роль при формировании теплового режима в рассматриваемой области и течении среды играет теплоотвод по внешним границам водоема. До настоящего времени моделирование конвективного теплопереноса, учитывающего влияние внешней среды на характер течения и температурное поле объекта, не проводилось.
Целью работы является математическое моделирование смешанной конвекции жидкости в водоеме с работающим тепловым насосом при различных условиях теплообмена на свободной поверхности.
Задача конвективного теплопереноса сформулирована для прямоугольной полости с теплообменником-испарителем теплового насоса, имеющей участки ввода и вывода жидкости и одну свободную поверхность. Область решения представлена на рис. 1.
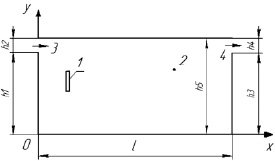
Рис. 1. Область решения задачи: 1 – теплообменник-испаритель; 2 – водоем; 3 – участок ввода жидкости; 4 – участок вывода жидкости
При моделировании предполагалось, что теплофизические свойства жидкости и материала стен не зависят от температуры. Жидкость считалась теплопроводной, вязкой, ньютоновской, удовлетворяющей приближению Буссинеска. Режим течения – ламинарный, границы полости (за исключением участков ввода и вывода воды) – непроницаемы. Не учитывался отток массы за счет испарения со свободной поверхности. В начальный момент времени принималось, что температура во всей рассматриваемой области постоянна и одинакова.
Эти допущения не вносят в постановку задачи значительных ограничений, но позволяют упростить ее решение. Температура теплообменника-испарителя остается неизменной в течение всего процесса. Внешние стенки принимались теплоизолированными.
На участке ввода массы (рис. 1) горизонтальная скорость принималась постоянной, на выходе из полости приняты условия симметрии по продольному направлению.
Положение источника теплопоглощения изменялось согласно схеме на рис. 2.
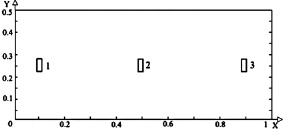
Рис. 2. Местоположения теплообменника-испарителя теплового насоса в водоеме
Отметим, что в реальных водоемах возможна реализация трехмерных распределений температур и компонент скоростей, но в рассматриваемой задаче поперечная составляющая скорости будет меньше двух других компонент, соответствующих основной плоскости движения вводимой в резервуар воды. Поэтому можно считать принятое допущение о двухмерной постановке задачи обоснованным.
Процесс переноса тепла в жидкости (рис. 1) для принятой физической модели описывается системой нестационарных двухмерных уравнений Навье – Стокса в приближении Буссинеска с нелинейными граничными условиями [2, 5]. Задача решалась в безразмерной постановке, аналогично [4, 7].
Исследовалось влияние условий на свободной поверхности жидкости на смешанную конвекцию в водоеме, в который сбрасываются воды промышленных энергоисточников. Численное решение задачи проводилось при следующих значениях безразмерных величин и температур: Re = 1000, Gr = 106, Pr = 7,1, Te = 258К, Tin = 313 К, Ti = 274 К.
На рис. 3 и 4 представлены линии тока и температуры для режима смешанной конвекции в водоеме с теплообменником-испарителем теплового насоса и участками ввода и вывода жидкости с различными внешними условиями на свободной поверхности, соответствующие осеннему и зимнему периоду.
 а
а 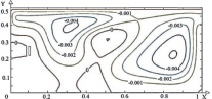 б
б
 в
в 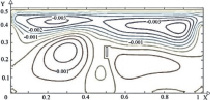 г
г
 д
д  е
е
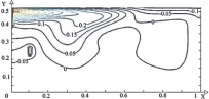
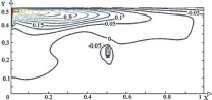
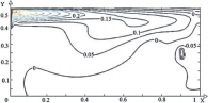
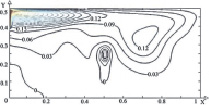
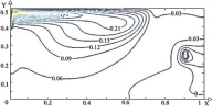
Рис. 3. Поле температуры (а, в, д) и линиии тока (б, г, е) в зимний период года при Re = 1000, Gr = 106, Tin = 313 K и различных положениях теплообменника-испарителя теплового насоса: а, б – положение № 1; в, г – положение № 2; д, е – положение № 3
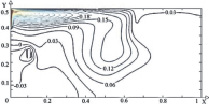
Следует отметить, что при различных положениях теплообменника-испарителя теплового насоса как в зимний (рис. 3), так и в осенний (рис. 4) периоды года характерны практически одинаковые циркуляционные течения.
При расположении источника в левой части (рис. 3, а, б и 4, а, б) исследуемой области образуется основной вихрь в правом нижнем углу. В случае, когда теплообменник располагается по центру (рис. 3, в, г и 4, в, г), формируется ряд низкотемпературных циркуляционных зон в угловых частях по обе стороны от стока тепла.
В обоих случаях хорошо выражена температурная неоднородность по глубине водоема и существует вероятность обмерзания теплообменника. Смещение теплообменника в правую часть (рис. 3, д, е и 4, д, е) приводит к формированию одного обширного циркуляционного вихря и, соответственно к интенсивному перемешиванию масс жидкости по всему объему водоема.
Анализ результатов (рис. 3 и 4) позволяет говорить об идентичности циркуляционных течений в водоеме при различных местоположениях теплообменника-испарителя теплового насоса в зимний период циркуляционным течениям осенью, тогда как численные значения температур значительно отличаются. В зимний период года происходит интенсивный отвод энергии со свободной поверхности. Отток теплоты вглубь водоема практически не происходит, основной поток теплой воды сохраняет направленное течение потока вдоль свободной поверхности.
 а
а 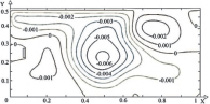 б
б
 в
в 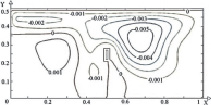 г
г
 д
д  е
е
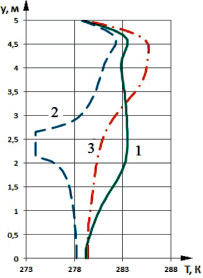
На рис. 5 представлены профили температур в центральном сечении полости при х = 0,5. Сравнивая профили температур для осеннего и зимнего периода, видно, что при более холодных климатических условиях происходит снижение температур в центральном сечении.
Проводя анализ влияния внешних условий на свободной поверхности жидкости на режим смешанной конвекции, следует отметить, что при понижении температуры окружающей среды температурное поле водоема значительно изменяется. При расположении теплообменника в средней части температура в осенний период остается равной начальной Т = 283 К, тогда как в зимний период она не превышает Т = 279 К. При этом внешние условия не влияют на интенсивность теплоотвода на трех внешних границах, кроме свободной поверхности жидкости (рис. 6).
Анализ влияния числа Рейнольдса на значения среднего числа Нуссельта на свободной поверхности жидкости проводился с использованием формулы [6]:
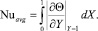
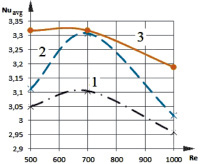
При анализе безразмерного коэффициента теплообмена на всех границах рассматриваемой области установлено, что теплообмен между жидкостью и окружающей средой осуществляется преимущественно через верхнюю (рис. 6) свободную границу. Числа Нуссельта значительно отличаются в осенний и зимний периоды. Например, в осенний период при Re = 1000 (положение 2) Nuavg = 3,1; в зимний период (положение 2) Nuavg = 3,5.
Заметно (рис. 6), что с увеличением числа Re значения безразмерного коэффициента теплообмена для всех вариантов расположения теплообменника испарителя изменяются не однозначно. Например, зависимость Nuavg = f(Re) для свободной границы области решения при центральном размещении теплообменника отличаются своей немонотонностью для двух различных периодов года (зависимости (2) на рис. 6, а и б).
 а
а 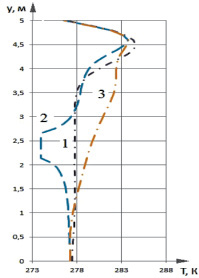 б
б
Рис. 5. Распределения температур в сечении, проходящем по центру полости (x = 5 м) при различных расположениях теплообменника-испарителя теплового насоса в осенний (а) и зимний (б) периоды
 а
а 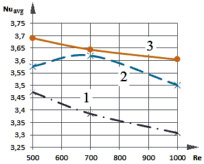 б
б
Рис. 6. Зависимость среднего числа Нуссельта Nuavg на свободной поверхности от числа Рейнольдса при различном расположении теплообменника-испарителя теплового насоса для осеннего (а) и зимнего (б) периодов
Хорошо проявляются точки излома. Такое расположение стока тепла при низких скоростях ввода воды препятствует продвижению потока жидкости с температурой Θ = 1 в центр рассматриваемой области. В осенний период года (рис. 6, а) безразмерный коэффициент теплоотдачи достигает своего максимального значения при Re = 700 для всех вариантов расположения теплообменника-испарителя. Можно отметить, что зависимости Nuavg = f(Re) изменяются при разных схемах размещения теплообменника-испарителя и разных условиях теплообмена на поверхности водоема.
Различные температурные периоды также приводят к изменению структуры течений и температурных полей в водоеме с теплообменником-испарителем. Расположение теплообменника влияет на интенсивность теплообмена между жидкостью и испарителем. Можно сделать вывод, что при смене положения стока тепла в водоеме соответственно изменяются и температурные режимы. Соответственно, при различных временах года необходимо менять расположение теплообменника в пространстве водоема для увеличения интенсивности теплообмена и уменьшения вероятности его обмерзания.
Работа выполнена в рамках НИР Госзадания «Наука» (Шифр федеральной целевой программы 2.1321.2014).
Рецензенты:
Кузнецов Г.В., д.ф.-м.н., профессор кафедры теоретической и промышленной теплотехники НИ ТПУ, г. Томск;
Стрижак П.А., д.ф.-м.н., профессор кафедры автоматизации теплоэнергетических процессов НИ ТПУ, г. Томск.
Работа поступила в редакцию 28.12.2014.



