Проектировщики разделительных аппаратов при проведении экспериментальных исследований материалов, подлежащих классификации, применяют труды [1]. Не секрет, что большой объем экспериментальных исследований не предполагает промышленной переработки исследуемых материалов. Так, с помощью результатов Н.К. Тимченко [2], полученных при обогащении щебня, спроектированы аппараты для разделения горных пород по упруго-фрикционным свойствам. В работе [1] описаны аппараты для предварительного обогащения углей, а в работе [3] – вибротранспортные машины для обогащения сыпучих материалов. Эти же результаты использованы П.М. Заикой [4] для виброочистительных машин.
Суть экспериментов Н.К. Тимченко состоит в измерении дальности полета горных пород после удара об обогатительную плоскость (рис. 1).
Из захвата 1 частицы горных пород падают без начальной скорости, имея к началу соударения с обогатительной наклонной плоскостью скорость падения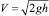 
. Затем происходит удар о наклонную плоскость 4. После чего частицы приобретают скорость, равную скорости отражения U, а затем отлетают по криволинейной траектории на горизонтальную плоскость 5.
Судя по расчетам, Н.К. Тимченко [2] использует максимум горизонтальной дальности частицы, для чего пытается эту дальность определить теоретически по формулам
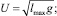(1)
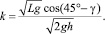(2)
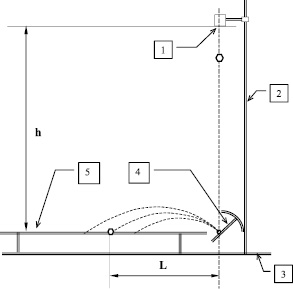
Рис. 1. Схема установки для изучения упругих свойств частиц горных пород: 1– захват; 2 – вертикальная стойка; 3 – основание корпуса установки; 4 – наклонная плоскость; 5 – горизонтальная плоскость
По приведенным формулам (1) и (2) автор полагает, что угол отражения частицы с горизонталью равен 45°, и обеспечивает максимальную дальность l, с которой начинается свободный полет частицы. Он, по-видимому, опирался на классическую задачу И.В. Мещерского под номером 27.49 [7] по определению угла начала полета снаряда с постоянной начальной скоростью, которая в данном случае неприемлема, так как в момент соприкосновения с наклонной плоскостью вектор скорости падения V0 составляет угол α0 с нормалью к этой плоскости, равный углу наклона рабочей поверхности φ (рис. 2). Таким образом, при первом ударе частицы о плоскость угол падения α0 = φ.
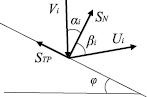
Рис. 2. Кинематические и силовые параметры частицы при ударе
Величину скорости после удара Ui и угол отражения βi при произвольном ударе «i» можно найти из системы уравнений, определяющих коэффициенты восстановления и трения при ударе, а также уравнений теоремы об изменении количества движения [5]:
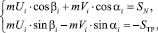(3)
где m – масса частицы, кг; SN, SТР – составляющие ударного импульса, Нс; Vi – скорость частицы перед i-м ударом о рабочую поверхность, м/с.
При этом коэффициент восстановления
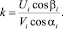(4)
Учитывая гипотезу Рауса [6], что ударный импульс трения равен произведению коэффициента трения на ударный нормальный импульс (т.е. направленный по нормали) SТР = fSN, получим выражение отношения ударных реакций.
Решая систему уравнений (3)–(4), получаем
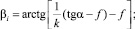(5)
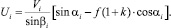(6)
После отражения частицы от наклонной поверхности происходит ее свободный полет. Если пренебречь силами сопротивления движению, уравнения свободного полета в системе координат, связанной с обогатительной плоскостью, можно получить из соотношений кинематики равнопеременного движения [5]: так как ax = g sin φ; ay = –g cos φ, то эти уравнения имеют вид
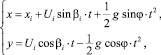(7)
где t – текущее время, которое определяется следующим образом:
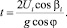(8)
Дальность полета li вдоль поверхности грохота до следующего удара находим, исключив из системы уравнений (7) параметр t при условии, что y = 0:
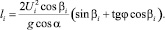(9)
Таким образом, получена истинная зависимость между дальностью полета рудной частицы и углом наклона обогатительной плоскости, дифференцируя которую и установим угол наклона плоскости, соответствующий максимальной дальности вылета частиц горных пород, далеко отличающийся от значения, приводимого Н.К. Тимченко.
Рецензенты:
Воротников В.И., д.ф.-м.н., профессор, заместитель директора по науке и инновациям, ФГБОУ ВПО «Нижнетагильский технологический институт (филиал) УрФУ» Министерства образования и науки Российской Федерации, г. Нижний Тагил;
Красовский А.Н., д.ф.-м.н., профессор, заведующий кафедрой информационных технологий и математического моделирования, ФГБОУ ВПО «Уральский государственный аграрный университет», г. Екатеринбург.
Работа поступила в редакцию 27.12.2014.