Диспергирующее усилие в электромагнитных механоактиваторах (ЭММА) формируется при силовом взаимодействии рабочих органов аппарата в магнитоожиженном слое, создаваемом в объеме обработкb материала под действием электромагнитных и механических сил
[6, 10, 11, 13, 14]. При прохождении через элементы ЭММА магнитного потока размольные тела организуются в различные структурные построения и создают магнитоожиженный слой, сцепляющий поверхности, ограничивающие объем обработки продукта [7, 9, 12]. При относительном смещении поверхностей структурные построения разрушаются. При этом мелющим телам сообщается кинетическая энергия движения в рабочем объеме аппарата. Процесс целенаправленной переориентации размольных элементов в структурных группах сопровождается созданием многоточечных контактных взаимодействий между ферроэлементами и частицами обрабатываемого продукта. Силовое воздействие проявляется как в виде усилий сжатия, так и ударно-истирающих нагрузок [1, 2, 3, 8]. Физико-математическое моделирование процесса формирования диспергирующих ударно-истирающих нагрузок между размольными ферроэлементами через прослойку перерабатываемого материала и анализ моделей априори способствует проектированию энергоэффективных ЭММА различного целевого назначения [4, 5].
Целью данной работы является теоретическое обоснование способа формирования ударно-истирающих нагрузок в магнитоожиженном слое ферротел ЭММА с разработкой физико-математической модели расчета энергетических затрат на ударное разрушение и статическое сжатие частиц обрабатываемого продукта.
Материалы и методы исследований
Предметом исследований является энергетика рабочего процесса формирования ударно-истирающих нагрузок в магнитоожиженном слое сферических размольных элементов ЭММА.
Результаты исследования
и их обсуждение
Фундаментальная теория, положенная в основу математического моделирования величины силовых контактов между ферромагнитными элементами в фазах рабочего процесса (формирование, разрушение структурных групп из ферроэлементов, образование «слоя скольжения»), построена на развитии дипольной модели Максвелла [5, 7, 12, 14]. Исследовав и установив количественные параметры энергетического процесса, происходящего с одной структурной группой из феррошаров, и умножив полученный результат на количество структурных групп в объеме обработки продукта, можно определить энергетику всего рабочего процесса формирования диспергирующих нагрузок в ЭММА. При расчетах число цепочек из ферромагнитных размольных элементов определяем по формуле 
(здесь NШ – количество размольных элементов сферической формы в рабочем объеме ЭММА; d – диаметр размольного элемента; h0 – расстояние от статора до ротора). При разработке линейной теории были сделаны следующие предположения: силы Fr и моменты Mv, действующие на намагничиваемый размольный элемент в рабочем объеме ЭММА, определены на основании развития дипольной модели Максвелла; диаметры размольных элементов много меньше ширины рабочего объема (d << h0) и много больше частиц обрабатываемого материала (d ˃˃ rч); cтруктурные группы из размольных элементов до момента их разрушения при достижении критического угла наклона структурной группы из феррошаров νкр при переходе в фазу образования «слоя скольжения» не взаимодействуют между собой.
С учетом исходного размера частиц rч силы Fr и моменты Mv, действующие на размольные элементы радиусом R0 в магнитном поле с напряженностью Н в рабочем объеме ЭММА, определены равенствами [1, 2, 5]:
(1)
(2)
Численное интегрирование дает следующие искомые выражения:
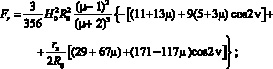(3)
(4)
В формулах (3) и (4) сохранены только линейные относительно
rч/Ro члены [1]. Критический угол νкр, при котором притяжение шаров сменяется их отталкиванием, определен
по формуле
(5)
Половина всех размольных элементов сжимается в структурной группе с силой Frmax. Работа, которую совершает эта сила, вычислена по формуле
(6)
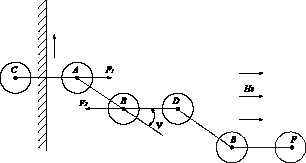
Рис. 1. Деформация структурной группы из размольных элементов в ЭММА.
Неравновесная структурная группа
Как это следует из рис. 2, на горизонтальных участках СА, ВД, ЕГ и т.д. сила сжатия максимальна. Формула для ее определения при νкр = 0 имеет вид
. (7)
Интегрирование формулы (3) с учетом равенства (7) дает
(8)
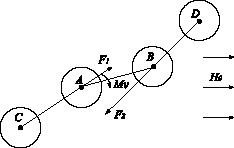
Рис. 2. Деформация структурной группы из размольных элементов в ЭММА.
Равновесная структурная группа
На участках АБ, ДЕ и т.д. угол наклона изменяется от 0 до νкр. Поэтому на этих участках сила притяжения шаров также меняется. Для простоты учета работы силы сжатия на этих участках принимаем некоторую среднюю силу, действующую на этих участках и соответствующую значению угла νкр:
(9)
Соответствующая этой силе работа определена формулой
(10)
Таким образом, работа, затрачиваемая на измельчение продукта от исходного размера зерна rч1 до конечного размера rч2 статическим сжатием между шарами, равна: Асж = А1 + А2. При разрушении структурной группы из феррошаров вся затраченная работа на изменение угла ν переходит в кинетическую энергию, которая расходуется на ударное разрушение продукта. Вращение объектов АВ, ДЕ и т.д. осуществляется за счет приложенного к ним момента Mν, который вычисляется по формуле (4). В этой формуле можно пренебречь отношением rч/R0 по сравнению с единицей:
M(ν) = F(ν)2R0 sin ν – Mν(ν). (11)
Работа, затраченная на поворот Nоб/2 объектов типа АВ на угол от 0 до π/6, определена равенством
(12)
Окончательная формула для вычисления работы ударного разрушения продукта имеет следующий вид:
(13)
Заключение
Физико-математическое моделирование процесса формирования диспергирующих ударно-истирающих нагрузок между размольными ферроэлементами в структурных группах через прослойку перерабатываемого материала и анализ моделей способствует повышению энергоэффективности проектируемых ЭММА различного целевого назначения.
Рецензенты:
Салова Т.Ю., д.т.н., профессор кафедры «Энергообеспечение предприятий» ИТССЭ, руководитель ведущей научной и научно-педагогической школы СПб «Системы, узлы и агрегаты двигателей»,
г. Санкт-Петербург;
Карпов В.Н., д.т.н., профессор кафедры «Энергообеспечение предприятий и электротехнологии» СПбГАУ, руководитель ведущей научной и научно-педагогической школы СПб «Эффективное использование энергии», г. Санкт-Петербург.
Работа поступила в редакцию 19.12.2014.