Математическое моделирование в экологии приобретает все большее значение, что может принести существенные результаты в области моделирования макродлительных экспериментов, прогнозировании и синтезе свойств исследуемой системы. В работе рассматривается моделирование тепловых полей на полигоне захоронения ТБО [5]. Температура является определяющим фактором, влияющим на химические и биологические процессы, протекающие в теле полигона [1, 2].
Целью представленной работы являлось моделирование процессов теплопереноса на полигонах ТБО.
Материал и методы исследования
При обосновании методов теплопереноса использовался метод конечных элементов, методы математического и имитационного моделирования. Объектом исследований являлись тепловые потоки, протекающие на объектах утилизации отходов, рассматриваемые как объекты моделирования и управления. Материалом исследования являлись твёрдые бытовые отходы.
Результаты исследования
и их обсуждение
Дифференциальная постановка задачи. Процесс теплопереноса на полигоне ТБО задан в области W в R3 c границей S, 
на части границы Si заданы граничные условия 1-го рода (изолированный экран), на части Sk заданы граничные условия 3-го рода (конвективный теплообмен) (рис. 1) [8, 9].
Уравнение теплопроводности в сплошной среде имеет следующий вид [2]:
(1)
где t – температура; КХХ, КУУ, КZZ – коэффициенты теплопроводности в направлениях х, у, z; Q – внутренний источник тепла, при граничном условии
(2)
где h – коэффициент теплообмена, кВт/м2; t – температура на границе; tос – температура окружающей среды; q – точечный источник тепла.
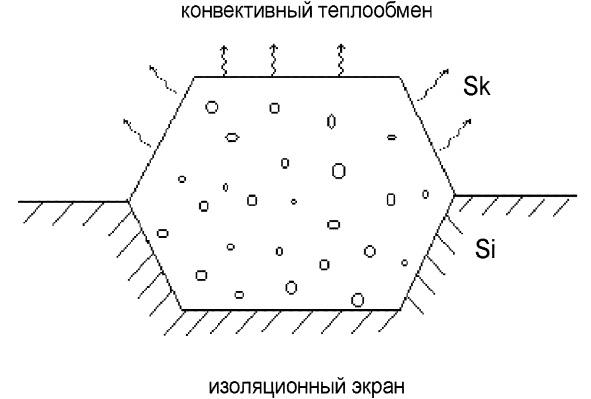
Рис. 1. Сечение полигона с граничными условиями 1-го и 3-го рода
Для нахождения приближенного решения дифференциальной задачи (1), (2) с помощью таких численных методов, как метод Ритца, Бубнова – Галеркина, конечных элементов (МКЭ), требуется построение вариационных аналогов исходных дифференциальных задач.
Вариационная постановка задачи. Вариационный аналог будет представлен минимизацией следующего функционала:
(3)
Для минимизации функционала на множестве узловых значений с различными характеристиками материала объемный интеграл должен быть представлен в виде суммы интегралов, каждый из которых вычисляется по отдельному элементу. Матрица теплопроводности элемента имеет следующий вид [12, 3]:
(4)
В качестве дискретного элемента для разбивки используем треугольный элемент. Функция формы для линейного треугольного элемента имеет вид
β = i, j, k. (5)
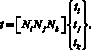(6)
Матрица градиентов [В]:
(7)
Матрица свойств материала [D]:
(8)
Теперь объемный интеграл примет следующий вид:
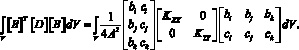(9)
Предполагая толщину элемента единичной, заменим dV на dA. Подынтегральное выражение в (9) постоянно и может быть вынесено за знак интеграла:
(10)
Вычисляя произведение матриц, имеем
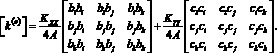(11)
Второй интеграл должен быть вычислен по поверхности:
Подставляя в матрицу [N] функции формы и выполняя матричное умножение, получаем
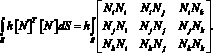(12)
Программная реализация
Для расчета температурных полей разработан пакет программ «work», предназначенный для определения стационарных и нестационарных температурных полей в плоских областях [4, 6, 7]. В пакете реализован стандартный метод конечных элементов (МКЭ), применяемый для решения различных задач теплопроводности. Функционально пакет разделен на две отдельные части: Grid – для разбивки рабочей области на конечные элементы; Vega – для решения плоской задачи теплопроводности. Рассмотрим основные этапы работы с программой «Work».
расчет теплофизических свойств фракций отходов
Для определения коэффициентов теплоемкости и теплопроводности использованы источники [11, 13] (таблица).
Теплофизические свойства фракций отходов
|
Компонент |
Теплопроводность, кал/(см∙с∙град) |
Теплоемкость, ккал/ кг |
|
Бумага |
144–308.10–6 |
3390 |
|
Пищевые отходы |
130.10–6 |
890 |
|
Дерево |
120.10–6 |
3410 |
|
Металл |
0,136 |
49 |
|
Стекло |
400–470.10–6 |
23 |
|
Резина |
500.10–6 |
5670 |
|
Камни |
2629.10–6 |
23 |
|
Текстиль |
95–120.10–6 |
3460 |
Разбивка рабочей области
на конечные элементы
Для разбивки рабочей области на конечные элементы (КЭ) необходимо предварительно разделить ее на зоны, каждая из которых образована восемью опорными узлами. Данную операцию можно провести либо вручную, либо с использованием специальных утилит для автоматического задания координат и номеров опорных узлов. До разбивки следует выполнить эскиз исследуемой области, выбрать необходимое число зон, опорных узлов, занумеровать зоны и узлы, нумерация сторон в каждой зоне ведется против хода часовой стрелки. Информация по разбивке формируется в файлах «Work» с расширениями in1, in2, in3. Далее запускается модуль «Maingrid». Происходит формирование файла граничных условий. Для формирования файла запускается программа «Bc_trm». Исходные данные для «Bc_trm» собирают в текстовом файле «Work.ggg». Расчет температурных полей создается в файле «Work.reg».
Для построения диаграммы температурных полей рис. 2 использована программа AXUM 5.0.
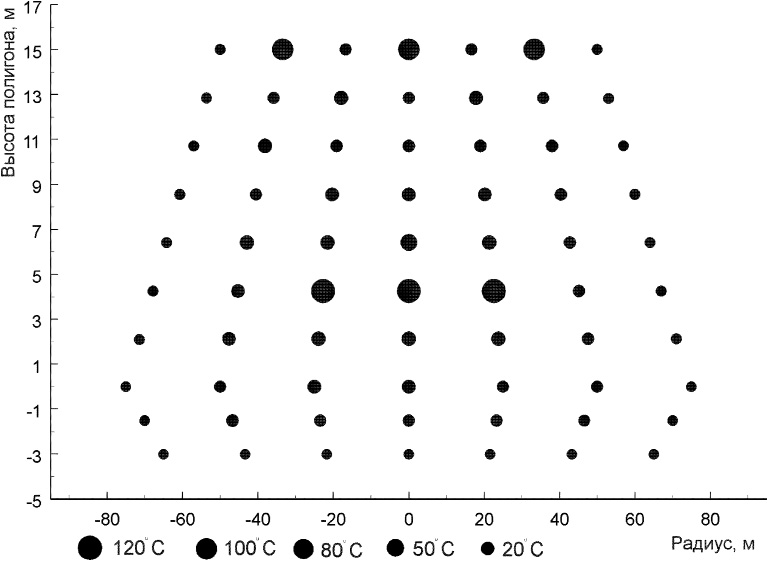
Рис. 2. Распределение температурных полей по сечению полигона
Применение методов системного анализа и кибернетики в управлении системами ПТО открывает возможность исследования и организации безопасного функционирования объекта депонирования ТБО в условиях, когда информация последовательно накапливается и реализуется в виде алгоритмов для ЭВМ. В этом случае управляющие действия будут направлены на минимизацию жизненного цикла природно-технических систем утилизации отходов, что имеет важное значение [14]. Внедрение автоматизированного рабочего места конструктора-проектировщика полигона ТБО уже на этапе проектирования позволит ускорить выполнение проектной документации и повысить безопасность эксплуатации природно-технической системы депонирования отходов на этапах её эксплуатации и рекультивации [8, 10, 15].
Рецензенты:Козлов В.В., д.т.н., профессор кафедры ВМКСиС, Пермский военный институт внутренних войск МВД России, г. Пермь;
Костарев С.Н., д.т.н., доцент, профессор кафедры «Строительное производство и материаловедение», Пермская государственная сельскохозяйственная академия,
г. Пермь.
Работа поступила в редакцию 19.12.2014.