Органическое вещество почвы (ОВП) очень неоднородно по химическому составу и кинетическим свойствам. В почве органическое вещество проходит огромное множество стадий трансформации. Точные формулы большинства соединений, количество стадий превращения, точные значения скоростей их трансформации не известны. Но известно, что общая направленность этого процесса – превращение вещества из малоустойчивого к трансформации в более устойчивое (гумификация), при этом часть вещества разлагается до CO2 и покидает почву (минерализация), и что скорости трансформации веществ, находящихся на разных стадиях гумификации, различаются на несколько порядков.
Обычно в математических моделях ОВП подразделяется на несколько компартментов, каждому из которых присущи свои скорости трансформации вещества. Фактически эти скорости являются усреднёнными значениями для большого количества веществ, относимых к данному компартменту. Многокомпартментные модели представляют собой системы обыкновенных дифференциальных уравнений, которыми описывается кинетика перехода вещества из одних компартментов в другие, а также кинетика минерализации вещества в каждом компартменте. Однако компартментному подходу присущи такие недостатки, как произвольность разделения на компартменты и сложность определения параметров моделей, состоящих из большого количества уравнений [3].
Континуальный подход к моделированию процессов трансформации детрита позволяет лучше выразить в модели многостадийность и огромное количество стадий трансформации. При таком подходе процесс трансформации органики описывается как перемещение вещества по некоторой шкале, отражающей устойчивость его к трансформации [6]. Применительно к трансформации ОВП континуальный подход был развит в работах Ågren и Bosatta
[3, 5]. Предложенная в них шкала качества субстрата позволила получить интегро-дифференциальное уравнение в частных производных общего вида, на основе которого было рассмотрено семейство моделей, описывающих динамику распределения ОВП по этой шкале. В этих моделях процесс трансформации ОВП описывался в явном виде, как результат деятельности сообщества почвенных организмов-разлагателей. Такое описание повлекло за собой существенное повышение сложности уравнений модели, использование в них значительного количества неизвестных или трудноопределимых параметров и функций, отражающих свойства сообщества разлагателей и химические характеристики трансформируемого субстрата.
Избежать явного описания механизмов трансформации ОВП и за счёт этого добиться существенного упрощения модели позволяет предложенное нами [4] использование величины скорости трансформации ОВП как шкалы его устойчивости.
В настоящей работе представлен и протестирован усовершенствованный вариант модели, представленной ранее в [4].
Уравнение модели
В предлагаемой модели весь многостадийный процесс трансформации и разложения органического вещества в почве описывается как замедляющееся перемещение вещества вдоль шкалы его гумифицированности, сопровождающееся минерализацией части вещества, скорость которой зависит от степени его гумифицированности.
Пусть C(h, t) – распределение запасов ОВП по скоростям гумификации h, меняющееся с течением времени t. То есть количество ОВП, имеющего в момент времени t скорость гумификации в пределах от h до h + dh, равно C(h, t)dh. Величина h в модели рассматривается как единственный показатель гумифицированности вещества, уменьшающийся по мере продвижения процесса гумификации. Это смещение влево по шкале h отражает превращение вещества в более устойчивые формы.
По модели, всякое органическое вещество в почве непрерывно претерпевает превращения, ведущие к уменьшению его h, происходящему со скоростью v(h):
![]() (1)
(1)
Знак «минус» здесь показывает, что реакция гумификации ведет к перемещению вещества в сторону меньших значений по шкале h.
Одновременно с гумификацией часть вещества подвергается процессу минерализации: разлагается и покидает почву со скоростью, равной −k(h)C(h,t), где k(h) представляет собой коэффициент скорости минерализации.
В момент времени t количество вещества cо скоростью гумификации h, лежащей в некотором диапазоне значений (h, h + Δh) будет равно C(h, t)Δh .
За время Δt часть этого вещества подвергнется гумификации и переместится по шкале h влево, а остальная часть его уйдёт из почвы в процессе минерализации. Следовательно, по закону сохранения вещества, количество ОВП в момент времени t в интервале Δh будет равно сумме количества органики, переместившейся из интервала Δh в интервал Δ′h (рис. 1) и количества органики, покинувшего почву в результате минерализации:
C(h,t)Δh + D(h, t)ΔhΔt = C(h−v(h)Δt, t + Δt) Δ’h + k(h)C(h, t) Δh Δt. (2)
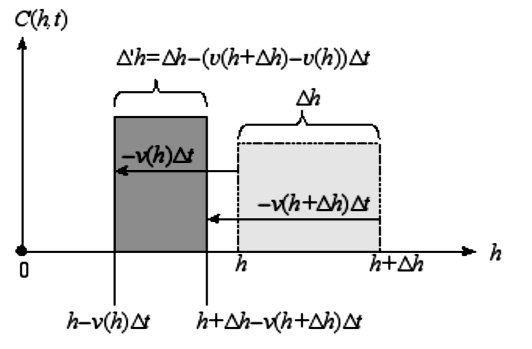
Рис. 1. Трансформация ОВП как движение вещества по шкале скорости гумификации h
Разлагая C(h−v(h)Δt, t + Δt) и v(h + Δh) в ряд Тейлора в точке (h, t), пренебрегая малыми членами разложения и подставляя в (2), получим уравнение динамики распределения ОВП:
![]() (3)
(3)
Принципиальное значение имеет задание функции v(h). Вид этой функции следует автоматически из выбора h в качестве шкалы. Величина v(h) – это скорость перемещения вещества по шкале скоростей реакции гумификации. При этом h является одновременно и шкалой гумификации (т.е. мерой трансформированности органического вещества в почве), и коэффициентом скорости реакции, результат которой – дальнейшее продвижение вещества по этой шкале. Таким образом, h одновременно является и изменяющейся величиной, и коэффициентом скорости изменения этой же величины.
Поэтому
![]() (4)
(4)
Также, чтобы выразить в уравнении (5) поступление органического вещества в почву с опадом, необходимо к члену −k(h)C(h,t), описывающему уход части вещества из почвы, добавить слагаемое D(h, t), представляющее собой распределение по h темпов поступления опада. И следовательно, общее уравнение модели трансформации ОВП примет вид
![]() (5)
(5)
Отметим, что опад может быть для удобства вычислений представлен в виде суммы нескольких его компонентов ![]() . И тогда, поскольку все органические вещества и почвы, и опада различаются в модели только по своим значениям h, уравнение (5) может быть выписано для каждого компонента опада в отдельности:
. И тогда, поскольку все органические вещества и почвы, и опада различаются в модели только по своим значениям h, уравнение (5) может быть выписано для каждого компонента опада в отдельности:
![]() (6)
(6)
а общее распределение всего ОВП будет суммой его решений ![]() .
.
Распределение запасов ОВП
при постоянном поступлении опада
Чтобы убедиться, что предложенное уравнение имеет решение, соответствующее реально наблюдаемым в природе почвенным параметрам, рассмотрим стационарное распределение ОВП по шкале h, вычислим значения запасов ОВП в стационарном состоянии и сравним их с имеющимися экспериментальными данными для различных экосистем.
В стационарном состоянии уравнение (5) примет вид
![]() (7)
(7)
где D(h) – распределение по h темпов поступления опада, предполагаемое неизменным во времени. В качестве D(h) могут быть взяты среднегодовые распределения количества опада по его начальной скорости гумификации.
Если опад может быть подразделён на несколько компонентов, для каждого из которых задано его среднегодовое количество D0i и его начальная скорость гумификации h0i, , то
![]() (8)
(8)
где δ – дельта-функция Дирака, а индекс i нумерует компоненты опада.
Решение уравнения (7) с D(h) в форме (8), удовлетворяющее также условию, что правее h0i по шкале h продуктов трансформации i-го вещества быть не может (ведь в модели движение по шкале происходит только в сторону уменьшения h), имеет вид
![]() (9)
(9)
где ![]() ; θ – функция-ступенька Хевисайда.
; θ – функция-ступенька Хевисайда.
Для вычисления распределения ОВП по h необходимо определить функцию k(h). В данной работе использована простейшая функция, при которой достигается совпадение модельных расчётов и экспериментальных данных:
k(h) = bhp, (10)
где b и p – константы, разные для разных экосистем. Подставив (10) в (9),
получим:
![]() (11)
(11)
Тогда количество запасов ОВП
![]() ,
,
где h0m – наибольшее из h0i.
Заметим, что при предположении неизменности во времени темпа поступления опада и задании его распределения в форме (8) уравнение динамики формирования распределения ОВП (5) име-
ет решение
![]() (12)
(12)
где функции fi определяются из граничных условий. Например, при условии, что правее h0i на шкале h никогда нет продуктов трансформации i-го компонента опада и что до момента t = 0 никакого органического вещества нет ни в какой точке шкалы,
fi(t − 1/h) = θ(t − 1/h + 1/h0i).
Результаты тестовых вычислений
Необходимый для проверки адекватности модели набор экспериментальных данных должен включать оценки:
1) запасов органического углерода в почве;
2) темпов поступления опада;
3) начальных скоростей его разложения, – полученные в одном месте.
Наличие экспериментальных данных, наиболее полно удовлетворяющих этому критерию, определило набор экосистем, использованных в работе для тестовых расчётов: северная, средняя и южная тайга [11, 12, 2], степь [1], серрадо [2, 10], влажный тропический лес [7, 8] (таблица).
Опад условно подразделён на две основные составляющие: 1-я – древесина и 2-я – лиственно-подобные компоненты, к которым отнесены как листья, так и все другие сравнительно легко разложимые компоненты. В использованной литературе данные об опаде приведены в единицах сухой биомассы. Пересчёт опада в углеродные единицы в таблице сделан приблизительно, в предложении, что количество углерода в опаде составляет половину его сухой массы. Значения h0i получены из значений скоростей минерализации опада k0i по вытекающей из (9) формуле
![]()
Экспериментальные оценки запасов ОВП в слое почвы толщиной 1 м, выраженные в углеродных единицах, взяты с карты [9], за исключением данных по тайге, взятых из работ [11, 12].
Результат подбора параметров модели b и p, при которых достигается приемлемое совпадение модельных расчётов стационарных запасов почвенного углерода S с экспериментальными оценками Snat, также приведен в таблице. Значение S вычислялось как интеграл распределения (11).
Параметры опада, подгоночные параметры модели, расчётные и наблюдаемые значения запасов ОВП в различных экосистемах
|
D01, |
D02, |
k01, год−1 |
k02, год−1 |
b |
p |
S, |
Snat, кгC/м2 |
|
|
Северная тайга |
0,07 |
0,10 |
0,011 |
0,09 |
0,56 |
0,69 |
9,3 |
9,3 |
|
Средняя тайга |
0,11 |
0,16 |
0,014 |
0,13 |
0,67 |
0,70 |
11,2 |
11,2 |
|
Южная тайга |
0,13 |
0,11 |
0,018 |
0,17 |
0,50 |
0,75 |
14,1 |
14,1 |
|
Степь |
– |
0,34 |
– |
0,33 |
0,55 |
0,90 |
15,0 |
15,2 |
|
Серрадо |
0,11 |
0,39 |
0,144 |
1,44 |
0,7 |
0,94 |
13,5 |
13,1 |
|
Тропический лес |
0,18 |
0,44 |
0,17 |
2,0 |
0,76 |
0,95 |
15,1 |
15,2 |
На рис. 2 показаны соответствующие этим параметрам распределения запасов ОВП по шкале h. Необходимо специально отметить, что графики построены в двойной логарифмической шкале. Это затрудняет адекватное восприятие графиков, но использование обычной шкалы ещё менее удобно, так как тогда все кривые распределения выглядели бы сливающимися друг с другом острыми пиками, вплотную прилегающими к оси ординат. Из-за двойной логарифмической шкалы кривые распределений тем больше растянуты по горизонтали, чем левее они расположены, и тем больше растянуты по вертикали, чем ниже они расположены. Вследствие этого для распределений с одним и тем же интегральным количеством ОВП высота максимума кривой будет тем больше, чем левее основная часть распределения расположена по оси абсцисс. Соответственно и площадь под кривой распределения, максимум которого расположен левее, выглядит на графике много большей, чем почти равная ей площадь под кривой, расположенной правее. Этим объясняется странное, на первый взгляд, расхождение площадей и высот распределений на рис. 2 с суммарным количеством органического углерода в почве из таблицы. Ступеньки на графиках на рис. 2 соответствуют появлению в распределении ОВП левее ступеньки продуктов трансформации компонента опада, имеющего при поступлении в почву начальное значение скорости гумификации h0i, равное координате ступеньки по оси абсцисс. Положение правой ступеньки на каждом графике соответствует точке поступления лиственно-подобного опада, положение левой – точке поступления древесного опада.
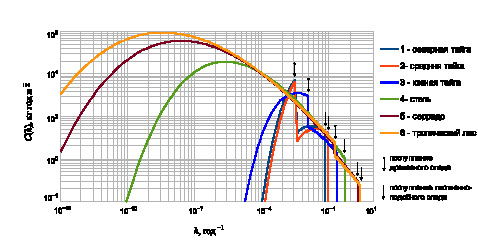
Рис. 2. Стационарные распределения ОВП C(h)
по скоростям гумификации h в рассмотренных экосистемах
Выводы
Предложенная континуальная модель трансформации ОВП, благодаря использованию скорости гумификации как континуальной шкалы трансформированности вещества, математически выражается в виде одного простого уравнения с малым количеством подгоночных параметров. Это уравнение имеет точное аналитическое решение в элементарных функциях, что является преимуществом предложенной модели по сравнению с другими существующими континуальными моделями трансформации ОВП. В настоящей работе продемонстрирована способность уравнения модели описывать реально наблюдаемые запасы органического вещества в почвах шести различных экосистем, что свидетельствует о применимости предложенной модели для описания почвенных процессов.
Работа выполнена при поддержке Интеграционного проекта СО РАН № 21.
Рецензенты:Суховольский В.Г., д.б.н., профессор, ведущий научный сотрудник лаборатории лесной зоологии Института леса им. В.Н. Сукачева СО РАН, г. Красноярск;
Садовский М.Г., д.ф.-м.н., профессор, ведущий научный сотрудник Отдела вычислительной математики Института вычислительного моделирования СО РАН,
г. Красноярск.
Работа поступила в редакцию 05.12.2014.



