Известно [1], что погрешность определения координат в навигационной аппаратуре потребителя (НАП) спутниковых радионавигационных систем (СРНС) прямо пропорционально зависит от погрешности измерения псевдодальности δR до каждого из навигационных спутников. Она определяется как сумма ее составляющих, обусловленных различными причинами: влиянием ионосферы (δRион), тропосферы (δRтроп), шумов приемника (δRшум) и целым рядом других факторов (δRдр):
δR = δRион + δRтроп + δRшум + δRдр. (1)
Наибольший вклад в погрешность определения псевдодальности δR = 30 м вносит ионосферная составляющая δRион ≈ 15 м и шумовая (δRшум), характеризуемая величиной среднеквадратического отклонения (СКО) 
. Для устранения ионосферной составляющей погрешности измерения псевдодальности (δRион ≈ 0 м) в СРНС «ГЛОНАСС» используются режим работы НАП на двух несущих частотах
(
, 
) и дифференциальный режим работы. Для уменьшения шумовой составляющей измерения псевдодальности до значений 
в СРНС используют широкополосные сигналы с шириной спектра ΔF0 = 1 МГц и ΔF0 = 10 МГц.
Однако при воздействии возмущающих факторов на слой F ионосферы (на высотах 150...300 км) возникают интенсивные флуктуации электронной концентрации (ЭК) в мелкомасштабных неоднородностях ионосферы, которые вызывают рассеяние радиоволн, их многолучевое распространение, замирания принимаемых сигналов и сужение полосы когерентности ионосферы до ΔFк < 0,1...1 МГц [2]. При распространении радиоволн через возмущенную ионосферу, например в результате выброса бария или радионагрева, на высоте слоя F принимаемые сигналы будут подвержены
частотно-селективным замираниям
(ЧСЗ), т.к. ширина спектра сигнала (ΔF0 = 1...10 МГц) может на порядок и более превышать полосу когерентности (ΔFк = 0,1...1 МГц) ионосферы (т.е. ΔF0 >>ΔFк), что приводит к уменьшению амплитуды отклика на выходе корреляционной схемы обработки принимаемого сигнала и увеличению шумовой составляющей погрешности определения псевдодальности 
. Однако вопросы исследования влияния ЧСЗ на точность определения псевдодальности и координат потребителя в [2] не рассматривались.
Цель статьи – оценка шумовой составляющей погрешности измерения псевдодальности 
в СРНС при возмущениях ионосферы в слое F.
Основная часть
Известно [3], что комплексная огибающая принимаемого сигнала отличается от комплексной огибающей передаваемого сигнала 
с энергией Et и нормированной комплексной огибающей 
лишь ослаблением амплитуды (в 
раз) и запаздыванием на время τ:
(2)
Потенциальная точность измерения времени запаздывания (τ) принимаемого сигнала sr(t) оптимальной некогерентной (НК) схемой его обработки на фоне гауссовских флуктуационных шумов определяется величиной среднеквадратического отклонения (СКО), описываемой выражением вида [4]
(3)
где 
– отношение энергии принимаемого сигнала Er к спектральной мощности шума N0, ΔΩэ – эффективная ширина спектра передаваемого сигнала, связанная с традиционной полосой спектра широкополосного сигнала с длительностью элементарных символов 
как 
. Анализ (3) показывает, что с увеличением ширины спектра передаваемого сигнала ΔF0 шумовая погрешность измерения времени запаздывания (τ) принимаемого сигнала 
уменьшается.
Оптимальная НК схема измерения τ согласно [3, 4] остается оптимальной в случае, когда принимаемые сигналы подвержены релеевским замираниям. При этом потенциальная точность измерения времени запаздывания (τ) принимаемого сигнала определяется выражением
(4)
где 
– средняя энергия принимаемого сигнала с ЧСЗ, равная его энергии в канале без замираний (Er = EtKoc); 
– мощность коэффициента передачи канала (b) с релеевскими замираниями. При обычно реализуемом в СРНС отношении сигнал/шум 
[5] выражение (4) сводится к виду (3).
Следует учесть, что релеевские замирания принимаемого сигнала являются частным случаем ЧСЗ, что позволяет обобщить известный метод оценки точности измерения времени запаздывания принимаемого сигнала (4) на случай приема сигнала с ЧСЗ. Комплексную огибающую принимаемого сигнала с ЧСЗ можно записать как [3]
(5)
где 
– нормированная комплексная огибающая передаваемого сигнала со средним временем запаздывания τ (неизвестная неслучайная величина, подлежащая измерению) и случайным запаздыванием λ; 
– низкочастотная импульсная функция канала связи (комплексный гауссовский процесс с математическим ожиданием 
и корреляционной функцией 
. Здесь σн(λ) – нормированная функция рассеяния КС по времени, связанная преобразованием Фурье с нормированной двухчастотной корреляционной функцией канала (зависящей от ΔFк).
Тогда потенциальная точность измерения времени запаздывания сигнала с ЧСЗ будет определяться выра-
жением [6]
(6)
где
(7)
– коэффициент энергетических потерь при корреляционной обработке сигнала с ЧСЗ,
(8)
– коэффициент сужения эффективной ширины спектра из-за ЧСЗ.
Коэффициенты энергетических потерь (7) и (8) зависят только от степени ЧСЗ принимаемого сигнала (ΔF0/ΔFк). В частном случае отсутствия ЧСЗ (ΔF0/ΔFк << 1), когда ηч = 1 и μч = 1, выражение (6) при 
сводится к виду (4). При выполнении условия возникновении ЧСЗ (ΔF0/ΔFк ≥ 1) значение στ(ч) > στ.
Выражение (6) с учетом (7), (8) можно записать в виде суммы двух слагаемых:
(9)
Анализ выражения (9) показывает, что для обычно реализуемого в СРНС отношения сигнал/шум 
второе слагаемое будет на порядок меньше первого при значениях ΔF0/ΔFк ≤ 102. Поэтому для указанных отношений формулу (9) можно записать в приближенном виде как
(10)
Качественный анализ (10) показывает, что при отсутствии возмущений ионосферы, когда полоса ее когерентности широка и намного превосходит ширину спектра сигнала (т.е. ΔF0/ΔFк << 1), шумовая погрешность измерения времени запаздывания широкополосного сигнала будет мала, т.к. 
. При сильных возмущениях ионосферы, когда полоса ее когерентности сужается до значений намного меньших ширины спектра сигнала (т.е.
ΔF0/ΔFк >> 1), шумовая погрешность измерения времени запаздывания широкополосного сигнала будет велика, т.к. 
. Следовательно, при известной полосе когерентности ионосферы (ΔFк) существует оптимальное значение ширины спектра передаваемого сигнала (ΔF0opt), при котором обеспечивается минимальное значение шумовой погрешности измерения времени запаздывания στ(ч)min.
Приравняв к нулю производную от функции στ(ч) (10) по ΔF0, получим уравнение, решение которого дает искомую формулу для выбора оптимальной ширины спектра передаваемого сигнала по КС с ограниченной полосой когерентности (ΔFк):
(11)
При оптимальной ширине спектра передаваемого сигнала (11) погрешность (СКО) измерения времени запаздывания сигнала с ЧСЗ (6) будет иметь минимальное значение
(12)
которое лишь в 33/4 ≈ 2,28 раз превышает погрешность измерения времени запаздывания (στ) сигнала без ЧСЗ (3).
Известно [7], что полоса когерентности трансионосферного канала связи, входящая в (7)–(8), определяется выражением
(13)
где f0 – несущая частота; ls – характерный масштаб неоднородностей; hэ – эквивалентная толщина ионосферного слоя; 
– СКО флуктуаций ЭК ионосферы относительно их среднего значения на высоте h = hm максимума ионизации 
; β – интенсивность неоднородностей; 
– коэффициент, характеризующий нарастание дифракционных эффектов во фронте волны по мере ее распространения, определяемый как
(14)
где h1 – расстояние от нижней границы ионосферного слоя до точки приема.
Воздействие различных факторов искусственного возмущения в слое F сопровождается ростом флуктуаций ЭК с σΔN(hm) = 109...1110 до σΔN(hm) = 1013...1114 эл/м3, т.е. могут составлять 3...4 порядка. В результате роста флуктуаций ЭК происходит пропорциональное сужение полосы когерентности трансионосферного канала связи (13) 
до значений ΔFк < 1 МГц.
Следует заметить, что аналогично (13) интервал пространственной когерентности трансионосферного канала связи также связан с СКО флуктуаций ЭК ионосферы обратно пропорциональной зависимостью: 
[8].
Поскольку в СРНС используются широкополосные сигналы с шириной спектра ΔF0 ≈ 1 МГц и ΔF0 ≈ 10 МГц, то при трансионосферном распространении радиоволн они могут подвергаться сильным ЧСЗ (т.к. 
). Искажения формы огибающей принимаемого сигнала из-за ЧСЗ 
, обусловленных увеличением СКО флуктуаций ЭК σΔN(hm), вызовут ее рассогласование с копией передаваемого сигнала, заложенной в корреляционном приемнике измерения времени задержки принимаемого сигнала (τ), и, как следствие – увеличение шумовой погрешности ее измерения στ(ч) из-за ЧСЗ.
С учетом (10) шумовая погрешность измерения псевдодальности при одночастотных измерениях будет определяться как
(15)
Двухчастотный режим работы (на несущих частотах f0в = 1,6 ГГц, f0н = 1,25 ГГц) позволяет полностью устранить ионосферную составляющую погрешности определения псевдодальности (δRион ≈ 0 м), но при этом (из-за наличия двух каналов корреляционной обработки сигналов с частотами f0в и f0н) в 2...3 раза возрастает шумовая составляющая, определяемая согласно выражению [5]
(16)
где 
– шумовая погрешность псевдодальности на верхней несущей частоте f0в = 1,6 ГГц; 
– на нижней несущей частоте f0н = 1,25 ГГц.
В дифференциальном режиме работа СРНС погрешности измерения псевдодальности, выполненные НАП и опорно-измерительной станции (ОИС), коррелированны во времени и в пространстве, за исключением шумовых погрешностей. Следовательно остаточная (после компенсации) погрешность измерения псевдодальности будет определяться СКО шумовой погрешности НАП и ОИС [9] и иметь вид
(17)
Так как ОИС работает в двухчастотном режиме, то выражение для расчета СКО шумовой погрешности измерения псевдодальности определяется выражением (16), т.е. 
Поскольку НАП работает в одночастотном режиме на несущей частоте f0в = 1,6 ГГц, то с учетом (15), (16) выражение (17) примет вид
(18)
Согласно (15)–(17) на рисунке представлены графики зависимости шумовой погрешности определения псевдодальности 
от СКО флуктуаций ЭК 
при неизменной ширине спектра передаваемого сигнала ΔF0 = 10 .
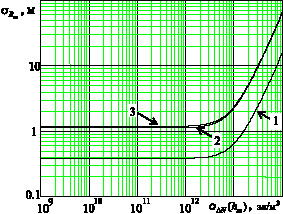
Графики зависимости шумовой погрешности определения псевдодальности 
от СКО флуктуаций ЭК σΔN(hm) в ионосфере при работе СРНС в одночастотном (1), двухчастотном (2) и дифференциальном (3) режимах
Из этих графиков видно, что при любой степени возмущения ионосферы σΔN(hm) шумовая погрешность 
при работе СРНС в одночастотном режиме (кривая 1) существенно ниже, чем при работе в двухчастотном (кривая 2) и дифференциальном (кривая 3) режимах работ, а шумовая погрешность измерения псевдодальности при работе СРНС в дифференциальном режиме лишь немного выше, чем при работе в двухчастотном режиме. При сильных возмущениях ионосферы, когда σΔN(hm) > 1012 эл/м3, во всех режимах работы СРНС значения 
могут возрастать на 1…2 порядка по сравнению с нормальной ионосферой, когда σΔN(hm) = 109...1010 эл/м3. Очевидно, что при выборе оптимальной ширины спектра сигнала (11) 
увеличение 
при сильных возмущениях ионосферы составило бы согласно (12) всего 2,28 раза по сравнению с нормальной ионосферой.
Заключение
При возмущениях ионосферы в слое F вследствие увеличения флуктуаций ЭК в мелкомасштабных неоднородностях ионосферы σΔN(hm) согласно (13) происходит сужение полосы когерентности трансионосферного канала 
, что приводит к выполнению условия возникновения ЧСЗ (ΔF0/ΔFк > 1) и увеличению погрешности измерения времени запаздывания принимаемого сигнала (10). Вследствие этого увеличивается шумовая погрешность
(
) измерения псевдодальности (15)–(17) в СРНС «ГЛОНАСС». В условиях возмущений ионосферы в слое F шумовая погрешность измерения псевдодальности может существенно возрастать (рисунок) по сравнению с условиями нормальной ионосферы, достигая значений 
в одноча-
стотном режиме НАП СРНС «ГЛОНАСС» и 
в двухчастотном и дифференциальном режимах работ. При выборе оптимальной ширины спектра сигнала (11) 
увеличение 
при сильных возмущениях ионосферы составило бы всего 2,28 раза по сравнению с нормальной ионосферой.
Жиляков Е.Г., д.т.н., профессор, зав. кафедрой, ФГАОУ ВПО «Белгородский государственный национальный исследовательский университет», г. Белгород;
Лубенцов В.Ф., д.т.н., профессор кафедры информационных систем, электропривода и автоматики Невинномысского технологического института, ФГАОУ ВПО «Северо-Кавказский федеральный университет» Минобрнауки РФ, г. Невинномысск.
Работа поступила в редакцию 05.12.2014.