Scientific journal

Fundamental research

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

В теории автоматического управления существует достаточно много методов, позволяющих оптимизировать работу систем по тем или иным критериям качества при выполнении ряда ограничений. Например, известно, что ПИД-регулятор считается достаточно близким к оптимальному, основанному на теории предсказания Колмогорова – Винера [6, 7, 8]. Однако может оказаться, что при возрастании требований к качеству управления объектами, функционирующими в переходных и установившихся режимах, быстродействие и динамическая точность регулирования с типовыми ПИ, ПИД-регуляторами и позиционными (релейными) регуляторами САУ становятся недостаточными. С позиций системного подхода практически все обычные системы должны быть отнесены к системам с неполной информацией о модели объекта. В связи с этим целесообразным становится использование методов интеллектуального управления, для которого характерен ряд преимуществ [2, 3, 5]. Приведем некоторые из них: во-первых, интеллектуальные системы сохраняют устойчивость при изменении параметров объекта управления в определенных пределах; во-вторых, они имеют существенно меньшую чувствительность к изменению параметров объекта управления по сравнению с оптимальными системами; в-третьих, интеллектуальное управление не требует точных математических объектов управляемых объектов, а в некоторых случаях позволяет обойти этап получения номинальной (расчетной) модели объекта; в-четвертых, на основе нечеткой логики позволяет использовать знания специалистов-наладчиков с целью настройки регуляторов в супервизорном режиме [1]. Однако в известных методах синтеза интеллектуальных систем с помощью нечетких регуляторов набор решающих правил является фиксированным и неизменным в процессе функционирования динамической системы. Модификация правил в случае ухудшения качества замкнутой системы невозможна без участия эксперта и не всегда согласуется со скоростью реакции системы, особенно при управлении быстро протекающими процессами.

В данной работе предложен подход к структурно-параметрическому синтезу системы программного управления и робастной стабилизации сложного объекта на основе методов нечеткой логики и переменной структуры. В основном контуре системы управления использован нелинейный регулятор с аппроксимирующей функцией управления, предложенный в работе [4]. Для программной системы, функционирующей в переходном и установившемся режимах, использованы два фаззи-блока с различным количеством термов, последовательно реализуемых в зависимости от состояния переходного процесса в системе. Причем в первом фаззи-блоке размещено меньшее количество термов, чем во втором фаззи-блоке, который срабатывает только после оценки состояния переходного процесса на заданном интервале времени и необходимости его улучшения после использования алгоритма нечеткой логики в первом фаззи-блоке.

Основная часть

Входными переменными предлагаемого фаззи-алгоритма являются ошибка регулирования (ε) и ее производная (dε/dt), а выходной переменной – значение корректирующего сигнала (λк) алгоритма управления. При синтезе системы использованы фаззификация треугольными функциями принадлежности и алгоритм логического вывода по Мамдани как наиболее простой и позволяющий выносить суждение о том или ином параметре в виде утверждений, в отличие от их представления линейными функциями, характерного для нечеткого вывода Сугено.

Для составления полного ряда правил и функций принадлежности используются общие знания о влиянии параметра λ алгоритма управления с аппроксимирующей нелинейной функцией [4] на переходные процессы и знания, полученные из проведения моделирования системы, об интервале значений [λmin, λmax] параметра настройки λ, обеспечивающих устойчивость системы. Это дает возможность начинать процесс подстройки параметра λ с использований рациональных значений, что ускоряет процесс поиска, особенно в условиях неопределенности. В лингвистических переменных нечеткой логики коррекция параметра λ в первом фаззи-корректоре представлена тремя термами: уменьшить (М), норма (Н) и увеличить (В). Для улучшения качественных характеристик системы рассмотрена более детальная нечеткая декомпозиция с пятью термами. Для этого в лингвистических переменных нечеткой логики коррекция параметра λ во втором фаззи-корректоре представлена следующими пятью термами: сильно уменьшить (СМ), уменьшить (М), норма (Н), увеличить (В) и сильно увеличить (СВ). Для перехода от нечетких выводов к корректирующему воздействию использована формула дефаззификации по методу центра тяжести.

Рассмотрим систему управления, обеспечивающую отслеживание входного задающего сигнала и стабилизацию объекта с помощью динамической коррекции параметра λк регулятора с аппроксимированной нелинейной функцией управления (нами обозначен как АНФ-регулятор) на основе переключаемых баз правил (БП). При этом реализованы две простые базы правил БП1 и БП2, состоящие соответственно из 3-х и 5-и терм. Границы переключения БП определяются сигналами, характеризующими качество исследуемой системы. На начальном этапе функционирования системы необходимо высокое быстродействие. Поэтому здесь целесообразно использовать БП2 с такими термами, как «сильно увеличить» или «сильно уменьшить», которые достаточно чувствительны к таким входным сигналам, как «скорость изменения входной переменной высокая», «ошибка регулирования большая» и т.д. Но недостатком такого управления являются большие значения выходного управляющего воздействия при приближении к заданному значению. На этом этапе целесообразно использовать алгоритм робастной стабилизации с другой базой правил, более чувствительный к ошибке регулирования. Поэтому по истечении некоторого времени имеет смысл переключить управление на менее форсированное – стабилизирующее, которое обеспечивается базой правил БП1, также достаточно простой. Для стабилизирующего управления характерно сильное замедление скорости изменения входного сигнала и уменьшение ошибки регулирования, что учитывается в БП1. Благодаря чему стабилизирующее управление позволяет более точно отследить задающий сигнал (без существенного перерегулирования).

На рис. 1 приведена структурная схема системы с двумя фаззи-корректорами и логическими блоками, обеспечивающими выбор и переключение БП. Для этого в системе задаются пороговые максимальный верхний Е1 и нижний Е2 уровни отклонения (ε) выходной переменной от задания, а также задается максимально допустимое время устранения отклонения (Т ≈ (3…5)Тр, где Тр – длительность переходного процесса). С учетом этого в блоке 1 вычисляются величины

S1 = max(/ε/ – E1) и S2 = max(/E2/ – /ε/),

на основании которых оценивается необходимость подключения фаззи-корректора с той или иной базой правил. При этом чем продолжительнее отклонение от порогового значения, тем большим должно быть корректирующее воздействие АНФ-регулятора. С учетом изложенного условия переключения реализованы в следующем виде:

если (/ε/ – E1) > 0 и Т ≥ 3Тр и БП = БП2 и λк = f1(ε, dε/dt),

то выбрать БП = БП1 иначе БП = БП2;

если (/E2/ – /ε/) < 0 и Т ≥ 3Тр и БП = БП1 и λк = f2(ε, dε/dt),

то выбрать БП = БП2 иначе БП = БП1. (1)

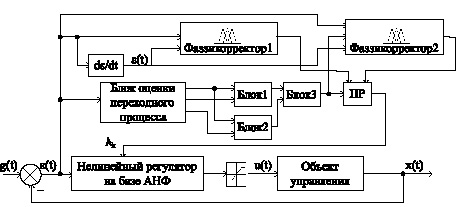
Рис. 1. Структурная схема системы управления с двумя фаззи-корректорами

Опишем кратко работу системы. Пусть в установившемся режиме на вход переключающего реле ПР поступает корректирующее воздействие λк с выхода фаззи-корректора 1. При превышении ошибкой регулирования первого порогового значения Е1 начинается отсчет времени блоком 2 и вычисление величин S1 и S2. В логическом блоке 3 проверяются условия переключения (1). При выполнении условий (1) блок 3 формирует командный сигнал на управляющий вход ПР, на второй вход которого подключен выход фаззи-корректора 2. В этом случае ПР осуществляет подключение выхода фаззи-корректора 2 на вход АНФ-регулятора, изменяя настроечный параметр λк в соответствии с новой базой правил. По истечении времени Т, равного 3Тр (Тр – время регулирования), величины S1 и S2 обнуляются и цикл повторяется заново.

Исследование переходных процессов проведено при подаче на вход системы скачкообразного изменяющегося сигнала задания g(t). В качестве объекта управления рассмотрен биореактор по каналу управления «расход хладагента – температура в реакторе». Объект управления представляет собой последовательное соединение апериодического звена второго порядка и звена запаздывания, его передаточная функция равна

Wоб(p) = 0,383·e–6p/(625,5p2 + 14,35p + 1).

Рассматриваемая система реализована с помощью среды MatLab версии 6,5. Исследование переходных процессов проведено при подаче на вход системы скачко­образного изменяющегося сигнала задания по закону:

На рис. 2, 3 приведены переходные процессы в программной системе управления с одной и двумя базами правил. В результате исследований установлено, что подбором условий переключения БП, определяющей веса корректирующих воздействий в зависимости от значений ε(t) и dε(t)/dt, можно получить монотонные переходные процессы и процессы без существенного перерегулирования с приемлемым временем регулирования. Как видно из рис. 2, на первом участке программы имеется нарушение нижней границы отклонения ошибкой регулирования. В течение заданного времени АНФ-регулятор с базой правил БП1 обеспечивает достижение заданного значения регулируемой переменной в колебательном режиме. При наличии в системе второй базы правил БП2 и при тех же условиях протекания переходного процесса на первом участке программы осуществляется подключение базы правил БП2, что обеспечивает более эффективную коррекцию параметра λ функции управления АНФ-регулятора, устранение колебаний и сокращение времени переходного процесса в 1,7 раза при его монотонном затухании. Однако переходный процесс на втором участке программы протекает с перерегулированием σ = 6,87 %.

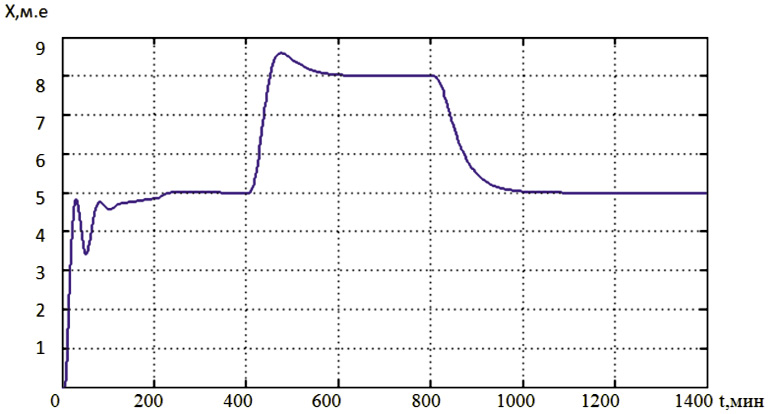
Рис. 2. Кривые переходных процессов в нечеткой системе программного
управления объектом 2-го порядка с базой правил:
на первом участке с БП1; на втором и третьем участках с БП2

В таблице приведены сравнительные оценки показателей качества переходных процессов в рассматриваемой системе управления и в системе с одной базой правил: максимальное динамическое отклонение – Аmax, величина перерегулирования – σ, степень затухания – ψ, длительность переходного процесса Тпп. Для системы с двумя БП в таблице приведены оценки показателей качества для наихудшего переходного процесса из представленных на рис. 2. Как видно из полученных оценок, переходные процессы в системе с двумя БП являются в основном либо монотонными, либо апериодическими на всех интервалах исследования системы. Такой характер переходных процессов объясняет большее время переходного процесса по сравнению с системой управления с нечеткой логикой на основе одной базы правил.

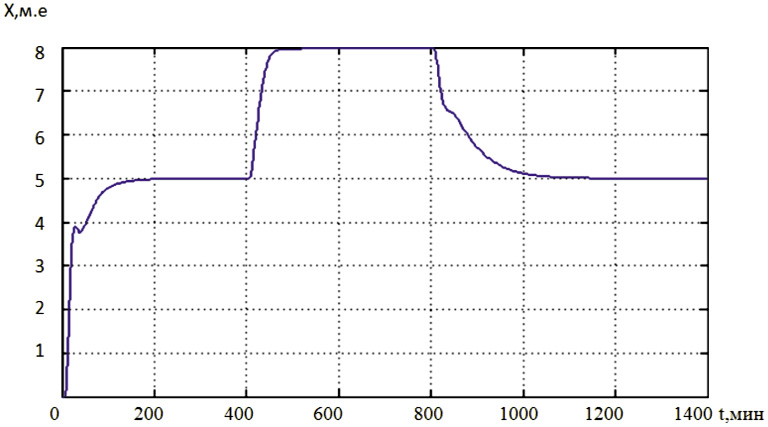
Рис. 3. Кривые переходных процессов в нечеткой системе
программного управления объектом 2-го порядка с базой правил:
на первом участке с БП2; на втором и третьем участках с БП1

Оценки показателей качества переходного процесса в системе
с нечетким АНФ-регулятором с двумя базами правил (БП)

Примечания: * степень затухания ψ = 1 соответствует апериодическому переходному процессу; ** нули в строке соответствуют монотонному переходному процессу (без перерегулирования). Совокупность всех правил для нечеткой переменной с функцией принадлежности с тремя термами обозначена базой правил 1 (БП1), а совокупность всех правил для нечеткой переменной с функцией принадлежности с пятью термами обозначена базой правил 2 (БП2).

Последовательность цифр 2-1-1, 1-2-2 и т.д. соответствует реализации баз правил второй, первой и первой или первой, второй и второй и т.д.

Заключение

Таким образом, из полученных результатов следует, что САУ с переключением баз правил значительно лучше справляется с двумя основными задачами: программным управлением и робастной стабилизацией объекта, поскольку обеспечивает наибольшее среднее качество управления и более высокую робастность по сравнению с САУ с одной базой правил. В результате исследований установлено, что подбором условий переключения баз правил, не увеличивая число лингвистических переменных и не расширяя БП, можно получить монотонные переходные процессы и процессы без существенного перерегулирования с приемлемыми показателями качества регулирования.

Червяков Н.И., д.т.н., профессор, заведующий кафедрой прикладной математики и математического моделирования, Институт математики и естественных наук, ФГАОУ ВПО «Северо-Кавказский федеральный университет» Минобрнауки РФ, г. Ставрополь;

Калмыков И.А., д.т.н., профессор кафед­ры информационной безопасности автоматизированных систем, Институт информационных технологий и телекоммуникаций, ФГАОУ ВПО «Северо-Кавказский федеральный университет» Минобрнауки РФ,
г. Ставрополь.

Работа поступила в редакцию 05.12.2014.