Рассмотрим систему квазилинейных уравнений вида
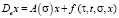 (1)
(1)
с дифференциальным оператором
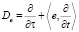 , (2)
, (2)
где А(σ) – гладкая и периодическая по σ∈Rm с вектор-периодом ω = (ω1,…, ωm) n×n – матрица
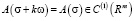 ,
, 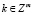 , (3)
, (3)
k = (k1,…, km)∈Z×…×Z = Zm, Z – множество целых чисел, kω = (k1ω1,…, kmωm) – кратный вектор-период, τ∈(– ∞, + ∞) = R, t = (t1,…, tm)∈R×…×R = Rm, 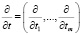 – символический вектор, e = (1,…,1) – m – вектор,
– символический вектор, e = (1,…,1) – m – вектор, 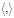 – знак скалярного произведения векторов, σ = t – eτ – базовая характеристика оператора De.
– знак скалярного произведения векторов, σ = t – eτ – базовая характеристика оператора De.
Предполагается, что вектор-функция f(τ, t, σ, x) обладает свойствами:
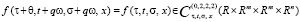 (4)
(4)
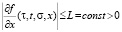 (5)
(5)
При условиях (3)–(5) начальная задача Коши имеет единственное решение с глобальной продолжительностью.
Ставится задача об исследовании существования и единственности (Ɵ, ω, ω) – периодических решений x = x(τ, t, σ) квазилинейной системы (1) в терминах собственных значений матрицы A(σ) путем приведения к каноническому виду.
Линейной неособенной заменой:
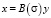 (6)
(6)
с (n×n)-матрицей B(σ) из такого же класса что и A(σ) систему (1) приводим к системе:
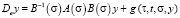 , (7)
, (7)
где 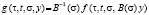 .
.
Очевидно, что если возможно выбрать матрицу B(σ) так, чтобы матрица подобия
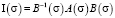 (8)
(8)
имела жорданову каноническую форму, то поставленная задача для системы (1) решалась бы довольно просто. В связи с этим возникает необходимость рассмотрения вопроса о приведении гладкой многопериодической матрицы (3) к жордановой канонической форме I(σ) преобразованием подобия (8).
Задача такого характера рассматривалась в связи с различными проблемами теории дифференциальных уравнений в работах [1]–[9].
В дальнейшем точки t∈Rm и t + kω, k∈Zm рассматриваются как идентичные. Совокупность таких точек Tm называется m – мерным тором. Справедливы следующие леммы.
Лемма 1. Если уравнение 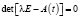 при условии (3) имеет l различных собственных значений λα(t),
при условии (3) имеет l различных собственных значений λα(t), 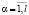 с независящими от t∈Rm кратностями nα, то собственные функции λα(t) обладают свойствами многопериодичности и гладкости.
с независящими от t∈Rm кратностями nα, то собственные функции λα(t) обладают свойствами многопериодичности и гладкости.
Лемма 2. Если выполнены условия леммы 1 и ранг rα матрицы λα(t)E – A(t) не зависит от t∈Tm при каждом 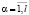 , то матрица A(t) подобна матрице
, то матрица A(t) подобна матрице
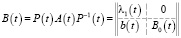 (9)
(9)
с некоторой неособенной матрицей преобразования 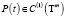 , где λ1(t) – собственная функция матрицы A(t), 0 – нулевая строка, b(t) – вектор-функция, B0(t) – квадратная матрица порядка (n – 1), причем
, где λ1(t) – собственная функция матрицы A(t), 0 – нулевая строка, b(t) – вектор-функция, B0(t) – квадратная матрица порядка (n – 1), причем 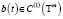 и
и 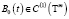 .
.
Далее, предположим, что матрица B0(t) из (8) приводится к ω – периодической гладкой жордановой канонической форме 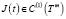 периодическим гладким преобразованием подобия:
периодическим гладким преобразованием подобия:
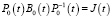 , (10)
, (10)
где 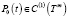 ,
, 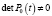 , t∈Tm,
, t∈Tm, 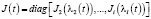 – жорданова форма с nα – клетками вида
– жорданова форма с nα – клетками вида
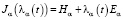 ,
, 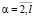 ,
,
Hα – матрица, у которой поддиагональные элементы – единицы, а остальные – нули, Eα – единичная матрица.
Теорема 1. Пусть выполнены условия леммы 2 и условие (9), тогда матрица A(t) ω – периодическим гладким преобразованием подобия приводится к виду
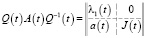 , (11)
, (11)
где
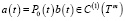 .
.
Рассмотрим матрицу
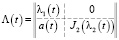 , (12)
, (12)
где λ1(t), λ2(t) – скалярные функции, a(t) = (a1(t),…, an(t)) – столбцовая вектор-функция, J2(λ2(t)) – жорданова n×n – клетка, соответствующая λ2(t), t∈Tm.
Лемма 3. Если λ1(t) ≠ λ2(t), 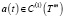 , то матрица (11) ω–периодической гладкой матрицей Q(t) приводится к жордановой канонической форме:
, то матрица (11) ω–периодической гладкой матрицей Q(t) приводится к жордановой канонической форме:
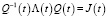 , (13)
, (13)
где J(t) = diag[λ1(t), J2(t) λ2(t))] и Q(t) – матрица преобразования вида:
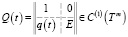 (14)
(14)
с единичной n – матрицей E и неизвестной столбец-функцией 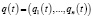 .
.
Далее, для обобщения леммы 3 рассмотрим матрицу
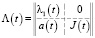 , (15)
, (15)
где λ1(t) – скалярная функция, J(t) = diag[J2(λ2(t)),..., Js(λs(t))] – Jα(λα(t)) – nα×nα – клетки Жордана, a(t) = (a2(t),...,as(t)) – 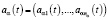 – заданные вектор-функции,
– заданные вектор-функции, 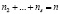 .
.
Лемма 4. Если λ1(t) ≠ λα(t), 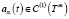 ,
, 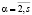 , то матрица (16) подобна матрице:
, то матрица (16) подобна матрице:
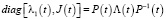 (15)
(15)
с некоторой неособенной матрицей
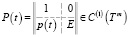 , (17)
, (17)
где p(t) = (p2(t),...,ps(t)), pα(t) = pα1(t),...,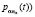 – вектор – функции,
– вектор – функции, 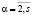 .
.
Теорема 2. Пусть выполнены условия леммы 2 и матрица A(t) имеет различные собственные значения, тогда существует неособенная матрица преобразования 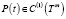 такая, что
такая, что
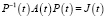 , (18)
, (18)
где J(t) – жорданова каноническая матрица.
Для доказательства теоремы используем метод математической индукции.
Таким образом, на основе лемм 1–4 и теорем 1, 2 система (1) приводится к каноническому виду
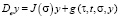 , (19)
, (19)
Матрица J(σ) имеет диагональный вид
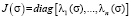 ,
,
причем предположим, что все собственные значения 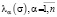 действительно значные различные и спектр не содержит нуля:
действительно значные различные и спектр не содержит нуля:
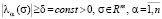 (20)
(20)
При условии (20) система (19) дихотомична и задача о ее многопериодическом решении имеет функцию Грина 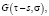 которая обладает свойствами :
которая обладает свойствами :
10. 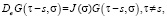
20. 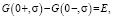
30.G(τ – s, σ + qω) = G(τ – s, σ), τ – s∈R, σ∈Rm, q∈Zm,
40. 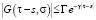 ,
,
где E – единичная матрица, Г ≥ 1, γ > 0 – некоторые постоянные.
Тогда задача о многопериодическом решении системы (19) имеет единственное решение 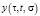 . Это решение определяется из интегрального уравнения:
. Это решение определяется из интегрального уравнения:
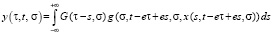 . (21)
. (21)
Тогда в силу замены (5) система (1) имеет единственное (θ, ω) решение.
Таким образом, имеем основную теорему.
Теорема 3. Пусть наряду с условиями теоремы 2 выполнены условия (4), (5) и (20). Тогда система (1) при достаточно малом L > 0 имеет единственное (τ, ω, ω) –периодическое решение
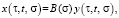
где 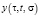 есть решение системы (19), определяемое интегральным уравнением (21).
есть решение системы (19), определяемое интегральным уравнением (21).
Заметим, что доказательство существования решения уравнения (21) приводится на основе принципа неподвижных точек для оператора
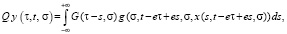
определенного в пространстве непрерывно дифференцируемых функций 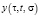 , ограниченных по норме:
, ограниченных по норме: 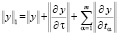 положительным числом ∆, где
положительным числом ∆, где  – знак нормы, максимизирующей модуль вектор-функции.
– знак нормы, максимизирующей модуль вектор-функции.
Бержанов А.Б., д.ф.-м.н., профессор, директор института прикладной математики Актюбинского регионального государственного университета им. К. Жубанова, г. Актобе;
Тасмамбетов Ж.Н., д.ф.-м.н., профессор, Актюбинский региональный государственный университет им. К. Жубанова, г. Актобе.
Работа поступила в редакцию 05.12.2014.



