Для фракционного осаждения частиц аэрозоля с целью определения их размеров и концентрации в дисперсионной среде используют импакторы (от impactum (лат.) – толкать, вталкивать). Существуют разнообразные конструкции этих устройств [2, 4]. Так, например, одним из наиболее распространенных является каскадный импактор Мэя. Работа импакторов основана на использовании эффекта инерционного движения частиц при резком изменении направления потока дисперсионной среды (воздуха). При изменении направления воздушного потока содержащиеся в нем частицы стремятся продолжить движение в прежнем направлении и сталкиваются с поверхностью, размещенной, как правило, перпендикулярно исходному направлению потока аэрозоля.
Воздух, несущий частицы аэрозоля, поступает в импактор с постоянной скоростью. Входное сопло первого каскада имеет самую широкую щель и на выходе из него скорость потока самая низкая. Апертура щелей от каскада к каскаду последовательно снижается, а скорость потока аэрозоля ступенчато возрастает до максимального значения на выходе из щели сопла последнего каскада. В щелевом импакторе частицы аэрозоля, достигшие препятствий – пластин, с нанесенным на них адгезионным слоем и установленных в каскадах импактора вплотную к апертуре щелей, – фиксируются на них. Количественным анализом определяют массу или количество осевших на пластинах частиц. По соотношению масс или числа частиц, осевших на разных каскадах импактора, определяют дисперсный состав аэрозоля, а с учетом времени отбора проб аэрозоля и расхода воздуха через импактор – пофракционную концентрацию аэрозольных частиц в воздухе.
Разработаны теоретические основы расчета импакторов, и проведены экспериментальные исследования по осаждению частиц аэрозоля на подложки (например, [1, 3, 5, 6]).
Целью настоящего исследования являлось:
– определение зависимости эффективности осаждения аэрозольных частиц на подложку каскада дискового импактора от апертуры щели, расхода воздуха, размеров частиц и их плотности, расстояния от щели до центра импактора;
– разработка методики расчета дискового импактора на основе полученных зависимостей эффективности осаждения частиц.
В исследовании использованы метод математического моделирования – описание движения аэрозольных частиц под воздействием воздушного потока дифференциальными уравнениями, и отчасти экспериментальный метод – проведен ряд испытаний разработанного на основе полученных теоретических соотношений дискового импактора на монодисперсных аэрозолях.
Оценим эффективность каскадов дискового импактора, в котором частицы аэрозоля проходят последовательно через каскады, представляющие собой концентрические щели. При этом расстояние от щели до центра импактора (радиус кривизны щели каскада) от каскада к каскаду уменьшается, а скорость воздуха возрастает.
На рис. 1 представлено сечение одного из каскадов дискового импактора.
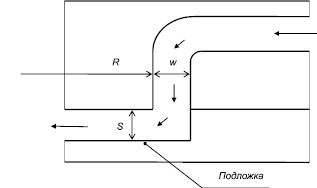
Рис. 1. Схема каскада дискового импактора
Скорость воздуха на входе в каскад равна
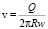 , (1)
, (1)
где Q – объемный расход воздуха, м3/с; R – расстояние от щели каскада до центра импактора (радиус закругления щелевого отверстия каскада), м; w – ширина щели каскада (апертуры сопла), м. Предполагается, что R >> w.
Максимальная эффективность импактора ε является отношением расстояния δ, на которое смещаются c линии тока в направлении подложки частицы, прошедшие каскад, к ширине апертуры сопла w:
ε = δ / w. (2)
Частицы с диаметром d будут смещаться с линии тока до тех пор, пока не потеряют свою первоначальную скорость в том направлении, которое они имели на входе в щель, т.е. нормально к поверхности осаждения. В общем случае это расстояние δ не больше расстояния S от среза щелевого отверстия каскада до подложки и равно расстоянию торможения частиц [3]:
δ = τv, (3)
где τ – время релаксации, которое можно рассчитать по формуле [3]:
τ = ρ1d2 Сс / (18 μ). (4)
В этой формуле: ρ1 – плотность частиц, d – их диаметр, Cc – поправка Каннингема, μ – динамическая вязкость воздуха.
Максимальная эффективность каскада импактора с учетом соотношения (3) определяется из выражения
ε = τv/w (5)
или для импактора с конструктивным соотношением размеров S = w:
ε = τv/S . (6)
Приведем пример, позволяющий оценить порядок значений характеристик импактора в отношении частиц аэрозоля с плотностью, близкой к плотности воды.
Пример. Входное щелевое отверстие импактора имеет радиус закругления R = 5·10-2 м и ширину щели w = 1·10-3 м. Определить расход воздуха через импактор, который необходим для полного осаждения частиц диаметром 10·10-6 м (10 мкм) и плотностью ρ1 = 1000 кг/м3 (1 г/см3). Динамическая вязкость воздуха при 20 °С и нормальном давлении равна µ = 1,83·10-5 Па·с.
Решение. Время релаксации частиц τ = ρ1d2 Сс /(18 μ) = 3,09·10-4 с. Так как максимальная эффективность каскада импактора ε = τv/w , то скорость и расход воздуха должны быть равными соответственно:
v = εw/τ = 1,0 ·1·10-3 /(3,09·10-4) = 3,24 м/с
и Q = 2πR·w·v = (6,28·5·10-2·1·10-3)·3,24 = 1,0210-3 м3/с (61,2 л/мин).
Все частицы со временем релаксации, большим, чем
τ+ = S / v, (7)
достигнут подложки и осядут на ней.
Учитывая формулу (4), связывающую время релаксации с диаметром частицы, из соотношения (7) можно найти минимальный диаметр d + частиц, которые все осядут на подложку каскада:
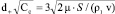 . (8)
. (8)
Анализ поля скоростей в щелевом импакторе показывает, что существует значение числа Стокса, равное 1/4 , ниже которого импакции частиц не происходит [3]. Правая часть в формуле (6) равна числу Стокса, так что получаем, что частицы с диаметром меньшим, чем
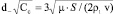 , (9)
, (9)
пройдут каскад, не оседая на его подложку.
Эффективность осаждения частиц с диаметрами ниже d+ будет уменьшаться в соответствии со следующим соотношением
ε = ρ1d2 Сс v / (18 μ S). (10)
Следует, однако, отметить, что расчет по формуле (10) может дать хорошее совпадение c экспериментальными данными лишь для частиц с диаметром больше некоторого d* , которое больше в свою очередь d – .
На основе полученных соотношений разработана методика расчета конструктивных параметров дискового импактора. Укрупненная схема алгоритма расчета параметров импактора для одного из вариантов методики представлена на рис. 2.
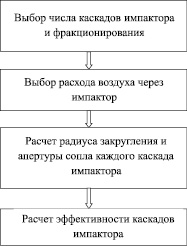
Рис. 2. Схема расчета конструктивных параметров дискового импактора
Следует отметить, что другой вариант методики предусматривает выбор максимального размера импактора (незначительно большего диаметра первого каскада) на начальных этапах расчета импактора с последующим расчетом необходимого расхода воздуха через него.
Используя разработанную методику, был произведен расчет геометрических параметров четырехкаскадного дискового импактора, предназначенного для фракционирования полидисперсного аэрозоля со сферическими частицами плотностью 1000 кг/м3 (1 г/см3) в диапазонах: свыше 10 мкм, от 5 до 10 мкм, от 2 до 5 мкм, менее 2 мкм. Расход воздуха через импактор был принят равным 20 л/мин. Изготовленный с найденными согласно методике геометрическими параметрами импактор был подвергнут испытаниям – проведены отборы проб монодисперсных аэрозолей с диаметрами частиц 14 мкм, 8 мкм, 4 мкм и 1,5 мкм и сравнение экспериментально найденных эффективностей каскадов дискового импактора с теоретически рассчитанными. Проведенные эксперименты позволяют утверждать, что отличие экспериментальных данных от расчетных не превышает 10 %. Это подтверждает применимость разработанной методики для расчета параметров дискового импактора.
Таким образом, в результате исследований получены соотношения, позволяющие по параметрам каскадов дискового импактора (радиусу закругления, ширине щели и расстоянию до подложки), диаметру и плотности частиц, расходу воздуха рассчитать эффективность каскадов импактора. Соотношения позволяют рассчитать конструктивные параметры каскадов, обеспечивающие максимальную эффективность осаждения на подложку частиц аэрозоля заданного размера и плотности. На основе теоретических соотношений разработаны варианты методики расчета дискового импактора, показавшие удовлетворительную согласованность расчетных эффективностей каскадов импактора с экспериментально найденными.
Рецензенты:Флегентов И.В., д.т.н., профессор, заведующий кафедрой промышленной экологии и безопасности, Вятский государственный университет, г. Киров;
Кучеренко А.С., д.т.н., доцент, главный научный сотрудник филиала ФГБУ «48 Центральный научно-исследовательский институт» Министерства обороны Российской Федерации, г. Киров.
Работа поступила в редакцию 05.12.2014.



