В настоящее время для ряда отраслей современной техники и технологии весьма актуальна проблема подавления акустических, ударных и детонационных волн в газах и жидкостях. Большое внимание к этой проблеме обусловлено необходимостью разработки эффективных мер борьбы с шумами в различных технологических и энергетических установках, а также необходимостью создания надежных систем защиты от взрыва, обеспечивающих безопасность труда и технологического оборудования. В связи с этим изучение отражения акустических волн от пористой преграды является весьма актуальным.
В [9] изучена эволюция волнового импульса при прохождении через пористую преграду, расположенную в газе и насыщенную таким же газом. В данной работе рассматривается случай, когда преграда находится в воде. Установлены закономерности отражения и прохождения волн через границу «вода – пористая среда».
Акустические волны используются при определении параметров призабойной зоны пласта [2, 5, 10, 14, 15], перфорированной зоны скважины [3, 6], а также нагрева пористых сред, насыщенных жидкостью [4, 8].
Основные уравнения
Пусть волновой импульс, распространяясь по жидкости, падает нормально на плоскую поверхность пористой среды, насыщенной газом. Толщина пористой среды (преграды) равна l (см. рис. 1), а два других её измерения, высота и ширина, достаточно большие, чтобы пренебречь краевыми эффектами. Поверхность преграды, на которую падает начальный импульс, будем считать первой границей, а параллельную ей и расположенную на расстоянии l – второй границей. В работе рассматриваются два различных случая, определяемые характером первой и второй границ:
а) «открытая» граница (в этом случае газ, содержащийся в порах, расположенных непосредственно на границе, соприкасается с водой, окружающей пористую среду);
б) «закрытая» граница (на границе между пористой средой и водой находится тонкая неподатливая плёнка нулевой массы).
Рис. 1. Схема пористой преграды
с датчиками D1 и D2
Когда волна падает на первую границу преграды, то одна часть волны проходит через границу в пористую среду, а другая часть – отражается. В пористой среде возникают две волны – «быстрая» и «медленная» [9]. «Медленная» и «быстрая» волны, распространяясь по пористой среде, достигают второй границы x = l. Часть каждой из этих («медленной» и «быстрой») волн отражается от второй границы, а другая часть – проходит через эту границу. В статье рассматриваются отраженная от первой границы и прошедшая через вторую границу волны.
Чтобы определить коэффициенты отражения и прохождения волны, сначала нужно рассмотреть распространение волны внутри преграды, т.е. в насыщенной газом пористой среде. Для описания исследуемого процесса примем следующие допущения: все поровые включения среды имеют сферическую форму и одинаковый радиус (характерными размерами среды будем считать средний радиус пор – a0 и среднюю полутолщину стенок пор – b0); значения длин рассматриваемых в среде волн намного больше размеров пор.
Запишем макроскопические линеаризованные уравнения неразрывности для скелета пористой среды и газа в порах в двухскоростном приближении:
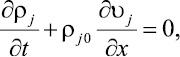(1)
где ρj, υj – плотность и скорость j–й фазы соответственно; нижним индексом j = s, g отмечены параметры скелета и газа в порах, дополнительным нижним индексом 0 – параметры, соответствующие невозмущенному начальному состоянию системы.
Уравнение импульсов для системы в целом запишем в виде
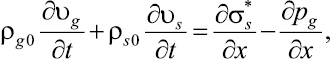(2)
где pg – давление в газовой фазе;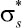 
– приведенное напряжение в скелете, определяемое через осредненное истинное напряжение 
:
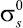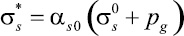; αs0 – начальная объемная доля твердой фазы. Верхним индексом 0 отмечены параметры, соответствующие истинным значениям.
Примем для скелета модель Максвелла. Тогда имеем
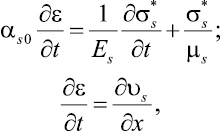(3)
где Es, μs – эффективные модуль упругости и коэффициент сдвига пористого скелета соответственно.
Уравнение импульсов для газовой фазы имеет следующий вид:
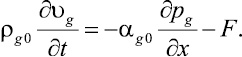(4)
Здесь αg0 – начальная объемная доля газовой фазы; F – межфазная сила взаимодействия [9].
Процессы диссипации тепла в изучаемой системе определяются распределением микротемпературы вблизи межфазных границ. Для описания микронеоднородностей температуры используется сферическая ячеечная схема, предложенная в работах [9]. При этом пористая среда, насыщенная газом, рассматривается как система сферических газовых пузырьков, окруженных слоем материала скелета. Таким образом, в каждой макроскопической точке, определяемой координатой x, вводится типичная ячейка, состоящая из газового пузырька и приходящейся на него доли скелета. Внутри ячейки имеется распределение температуры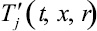 
и плотности газа 
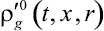(r – координата, отсчитываемая от центра ячейки). Давление внутри ячейки полагается однородным.
Связь между микроплотностью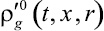 
и истинной плотностью 
,
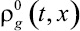являющейся средней для газовой фазы, определяется с помощью выражения [1]:
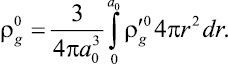(5)
Для истинных плотностей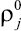 
и объемной доли фаз αj можно записать следующие кинематические соотношения: 
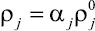, αg + αs = 1.
Для описания распределения температуры в ячейке пористой среды запишем систему уравнений теплопро-
водности:
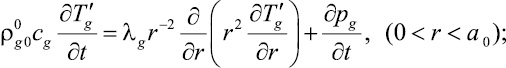
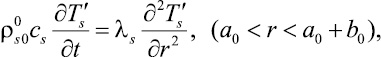(6)
где λj, cj (j = g, s) – теплопроводность и удельная теплоемкость.
Граничные условия для уравнений (6) запишем в виде
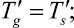
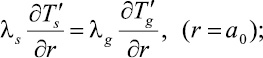
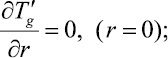
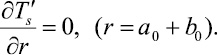(7)
Газ, находящийся в порах среды, будем считать калорически совершенным. Тогда
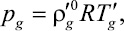(8)
где R – газовая постоянная.
Для бегущих гармонических волн в работе получено дисперсионное соотношение. Написаны условия для границы «вода – пористая среда» и получены коэффициенты отражения и прохождения.
Прохождение импульса давления
через преграду
С использованием полученных выражений для коэффициентов отражения и прохождения гармонических плоских волн на первой и второй границах рассмотрим эволюцию волны конечной длительности, проходящей через пористую преграду. В зависимости от толщины пористой преграды будем рассматривать импульсы давлений, временная протяженность которых позволяет не учитывать влияние отраженного от противоположной границы импульса на прохождение им рассматриваемой границы.
Пусть слева от преграды на границу раздела «вода – пористая среда» падает импульс давления, имеющий колоколообразную форму [7, 11–13]. В численных расчетах временная протяженность импульсного сигнала равна 2,5∙10–4 c, а толщина пористой преграды l = 0,5 м.
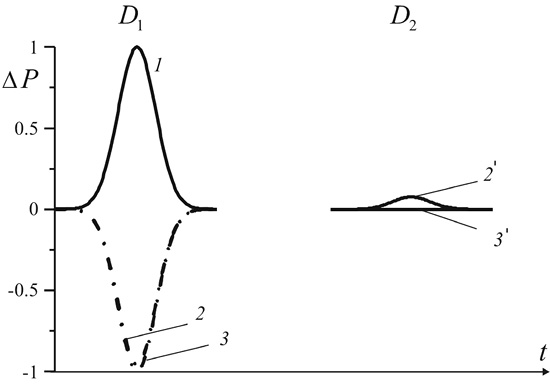
Рис. 2. Влияние состояния пор на границе преграды на эволюцию импульса давления.
Линия 1 – исходный импульс; линии 2 и 3 – отраженные от первой границы импульсы;
линии 2′ и 3′ – прошедшие через вторую границу импульсы. Линии 2 и 2′ соответствуют случаю, когда поры на границе закрытые, а линии 3 и 3′ – когда поры на границе открытые
Результаты численной реализации анализа процессов отражения и прохождения импульсных возмущений через пористую преграду с «открытыми» и «закрытыми» порами на границе, проведенной с использованием метода дискретного преобразования Фурье, представлены на рис. 2–3. Осциллограммы D1 и D2 соответствуют показаниям датчиков D1 и D2, расположенных перед пористой преградой и после нее. Датчик D1 регистрирует исходный и отраженный от первой границы пористой преграды импульсы давления, а датчик D2 – импульс, прошедший через вторую границу преграды.
Зависимость эволюции импульса давления от состояния пор на границе демонстрируется на рис. 2. Исходная объемная доля газа в пористой среде равна αg0 = 0,9. Когда поры на границе «открытые», то волна почти полностью отражается от первой границы (как от «свободной» границы). В этом случае эволюция импульса слабо зависит от радиуса пор и исходной объемной доли газа в среде.
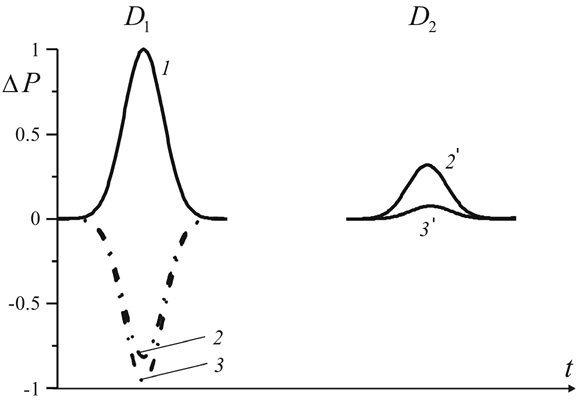
Рис. 3. Эволюция импульса давления, преодолевающего пористую преграду с закрытыми порами на границе. Линиям 2 и 2′ соответствует αg0 = 0,5, а линиям 3 и 3’ – αg0 = 0,9.
Остальные обозначения линий такие же, как на рис. 2
На рис. 3 показано влияние исходной объемной доли газа в пористой среде на значение амплитуды прошедшего через преграду импульса для случая «закрытых» пор на границе. Видно, что эволюция импульса существенно зависит от исходной объемной доли газа αg0. Установлено, что при уменьшении αg0 от 90 до 50 % величина амплитуды импульса, прошедшего через преграду, увеличивается от 10 до 40 % от исходной амплитуды. В этом случае эволюция импульса слабо зависит от радиуса пор.
Вывод
Установленные закономерности прохождения и отражения волн конечной длительности от насыщенной газом пористой преграды могут быть использованы при разработке средств защиты объектов от акустических, ударных и детонационных волн.
Работа выполнена при поддержке гранта СФ БашГУ № В14-19.
Рецензенты:Мустафина С.А., д.ф.-м.н., профессор кафедры математического моделирования, Стерлитамакский филиал, ФГБОУ ВПО «Башкирский государственный университет», г. Стерлитамак;
Михайлов П.Н., д.ф.-м.н., профессор кафедры алгебры, геометрии и методики обучения математике, Стерлитамакский филиал, ФГБОУ ВПО «Башкирский государственный университет», г. Стерлитамак.
Работа поступила в редакцию 28.11.2014.