Как известно, понятие «функция» в чистой и прикладной математике имеет различное содержание. В первом случае оно воспринимается как конкретное выражение одной переменной через другую; изучение функции сводится к изучению различных свойств этого выражения. В прикладной математике «функция», прежде всего, есть конечная последовательность арифметических действий, с помощью которых из заданного значения одной переменной можно получить значение другой переменной. «Функция» прикладной математики является моделью «функции» чистой математики. Замечательно, что есть множество функций, которые сами по себе являются моделями. Таким множеством является линейное пространство всех алгебраических многочленов или отношений многочленов.
Одной и той же функции можно сопоставить различные модели, выбор которой зависит от решаемой задачи. Для широкого класса функций с точки зрения возможности получения их значений с наперед заданной точностью за наименьшее количество арифметических действий (за наименьшее машинное время) наилучшими моделями являются подходящие дроби цепных дробей [7].
В настоящее время повышение интереса к теории цепных дробей объясняется еще и тем, что, несмотря на видимую громоздкость представления, процесс их вычислений является цикличным и легко поддаётся программированию при использовании ЭВМ.
1. Цепной (непрерывной) дробью, называется выражение вида
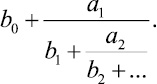(1)
Из-за громоздкости записи (1) цепная дробь записывается так:
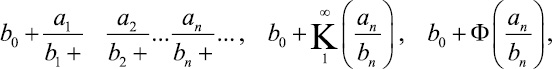(1)
где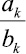 
– k-е звено цепной дроби; ak и bk – члены k-го звена; ak – частные числители, bk – частные знаменатели цепной дроби. Будем считать bk ≠ 0, k = 1, 2, ...
Конечная цепная дробь
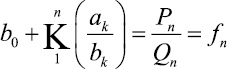
называется n-й подходящей дробью цепной дроби (1); Pn – числители; Qn – знаменатели подходящей дроби fn [4].
Имеют место рекуррентные соотношения (установлены Валлисом (1655 г.) и подробно изучались Эйлером (1737 г.))
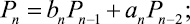
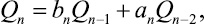(2)
n = 1, 2, .... При этом P–1 = 1, Q–1 = 0 [4].
2. Известно ([1]), что для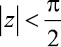 
функция tg z разлагается в степенной ряд
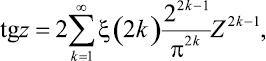
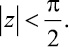
Здесь ξ(z) – дзета функция Римана.
В ([6]) доказано: для комплексных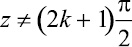 
, k-целое, справедливо разложение в цепную дробь
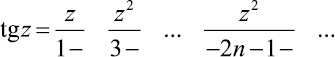(3)
Если Pn(z)/Qn(z) – подходящая дробь порядка n цепной дроби (1), то Q2k(z), Q2k+1(z), zP2k–1(z), zP2k(z) будут многочленами степени 2k. Так как Q1(z) = 1, Q2(z) = 3 – z2, то из ([2])
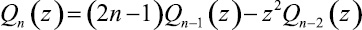
следует
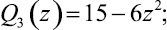
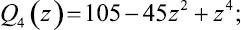
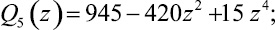
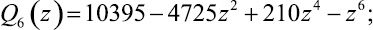
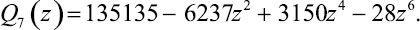
Заметим еще, что если ε1 = 1,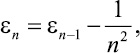
то ε2 = 0,75, ε3 = 0,64, ε4 = 0,54, ε5 = 0,50, ε6 = 0,48, ε7 = 0,46. Здесь значения εn округлены. Имеют место следующие две теоремы.
Теорема 1. Если при некотором x, 3x2 < 5 двойное неравенство
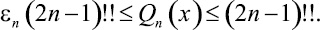(4)
имеет место для двух значений n = k и n = k + 1, k – некоторое число, то при тех же значениях x (4) останется в силе и при n = k + 2.
Следствие. При x2 ≤ 1,13 и n ≥ 1 имеет место двойное неравенство
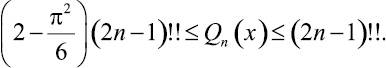(5)
Заметим, что ([7])
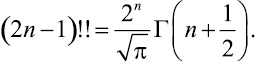(6)
Теорема 2. При x2 ≤ 1,13 будет
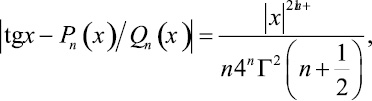
где an ≈ bn означает: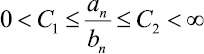 
; Γ – гамма функция Эйлера.
По значениям tg x можно вычислить sin x, cos x, используя формулы
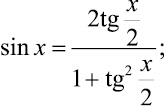
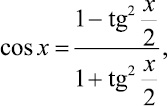
при помощи fn, где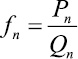 
вычисляются с использованием прямого рекуррентного алгоритма
P0 = 0; Q0 = 1;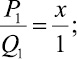 
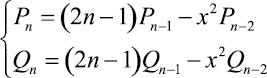при n ≥ 2.
Ниже приводится листинг программы, разработанной на языке Turbo Pascal для нахождения значений функций sin x и cos x, используя связь sin x и cos x с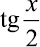 
,
с использованием подходящих дробей цепных дробей 7-го порядка для x = 0,1; 0,2; ...; 1,5 и указано приближенное значение этих функций с точностью
до шестнадцатого знака.
Листинг программы
Результаты программы
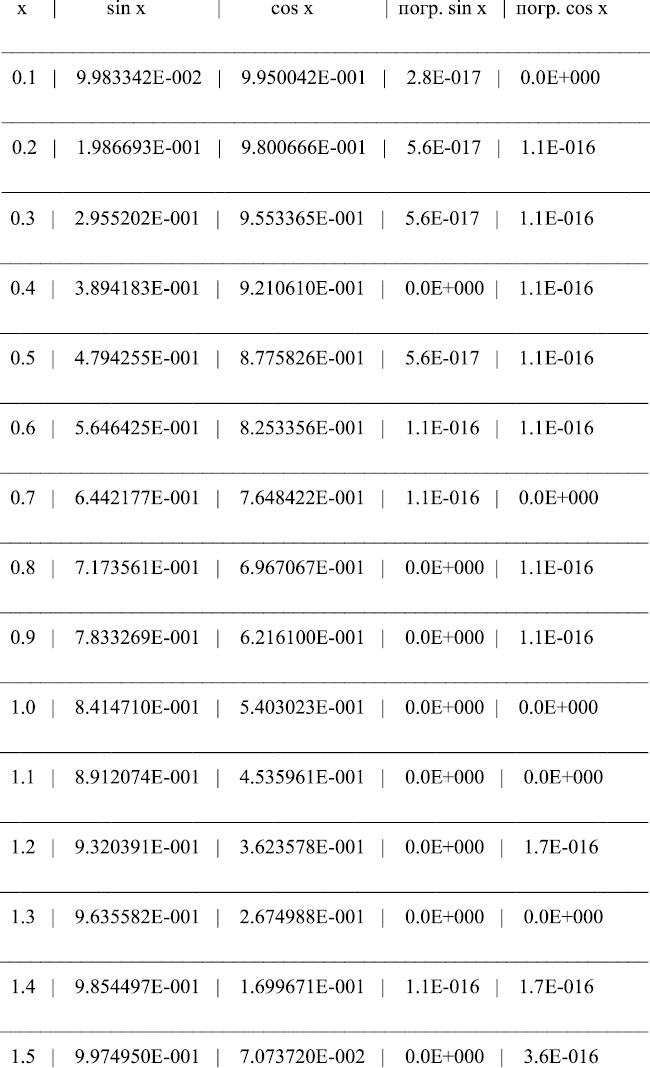
Из полученных значений для погрешностей видно, что данный способ интерполирования является более точным.
Рецензенты:Рамазанов А.-Р.К., д.ф.-м.н., профессор, заведующий кафедрой математического анализа, ФГБОУ ВПО «Дагестанский государственный университет», г. Махачкала;
Баламирзоев А.Г., д.т.н., профессор, ФГБОУ ВПО «Дагестанский государственный технический университет», г. Махачкала.
Работа поступила в редакцию 28.11.2014.