Изучение динамики незамкнутых кинематических цепей с конечным числом степеней свободы является актуальной задачей для различных областей науки и техники, например исследования динамики механических манипуляторов [5].
Целью данной работы является развитие методов исследования динамики незамкнутых кинематических цепей, а также разработка математической модели динамики механической системы шарнирно-соединенных стержней (рис. 1) с тремя степенями свободы. В работе решается частная задача по определению закона движения системы в обобщенных координатах.
Рассматривается механическая система, состоящая из трех абсолютно твердых стержней, длины которых обозначим l1, l2, l3. Стрежни соединены между собой шарнирами O1 и O2. Стержень 1 закреплен при помощи неподвижного цилиндрического шарнира O. На стержень 1 действует момент активных сил M.
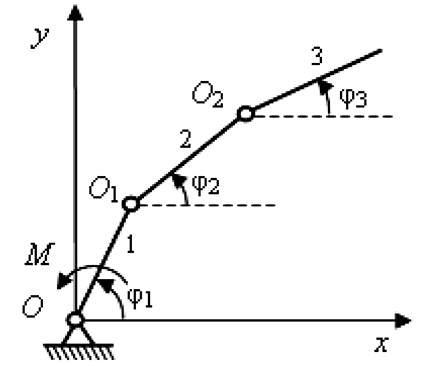
Рис. 1. Кинематическая схема:
1, 2, 3 – абсолютно твердые стержни;
О, O1, O2 – идеальные шарниры;
φ1, φ2, φ3 – углы поворота стержней;
M – момент активных сил
Задача решается при следующих предположениях:
– все шарниры являются идеальными (силы трения и их моменты отсутствуют);
– движение происходит в горизонтальной плоскости (силы тяжести не совершают работы);
– момент активных сил является постоянным M = const.
Для решения задачи об определении закона движения механической системы используется метод уравнений Лагранжа II рода [2, 4]. Система имеет три степени свободы. В качестве обобщенных координат выбраны углы поворота стержней φ1, φ2 и φ3. Таким образом, уравнения Лагранжа II рода можно записать в виде
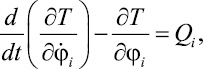 (1)
(1)
где φi – обобщенные координаты системы; 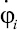 – обобщенные скорости; Qi – обобщенные силы; T – кинетическая энергия системы.
– обобщенные скорости; Qi – обобщенные силы; T – кинетическая энергия системы.
Кинетическая энергия системы определяется как сумма кинетических энергий трех стержней по формуле
T = T1 + T2 + T3, (2)
где T1 – кинетическая энергия стержня 1; T2 – кинетическая энергия стержня 2; T3 – кинетическая энергия стержня 3.
В работе [6] получены выражения для кинетических энергий стержня 1
и стержня 2:
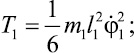 (3)
(3)
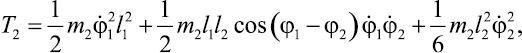 (4)
(4)
где m1 и m2 – массы стержней 1 и 2 соответственно.
Кинетическую энергию стержня 3 определим по формуле [2]
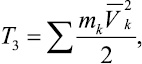 (5)
(5)
где mk – масса k-й точки стержня 3; 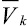 – вектор скорости k-й точки стержня 3.
– вектор скорости k-й точки стержня 3.
Скорость 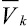 определяется теоремой сложения скоростей
определяется теоремой сложения скоростей
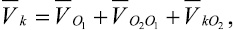 (6)
(6)
где 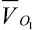 – вектор скорости шарнира О1,
– вектор скорости шарнира О1, 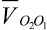 – вектор относительной скорости шарнира О2;
– вектор относительной скорости шарнира О2; 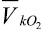 – вектор относительной скорости k-й точки стержня 3.
– вектор относительной скорости k-й точки стержня 3.
Подставляя (6) в выражение (5), получим
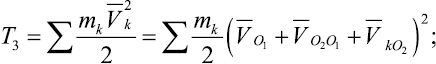
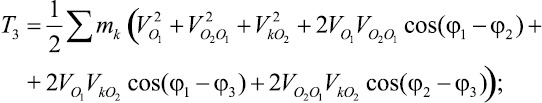
где φ1–φ2 – угол между векторами скоростей 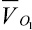 и
и 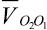 ; φ1–φ3 – угол между векторами скоростей
; φ1–φ3 – угол между векторами скоростей 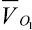 и
и 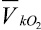 ; φ2–φ3 – угол между векторами скоростей
; φ2–φ3 – угол между векторами скоростей 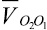 и
и 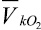 .
.
Запишем выражения для скоростей 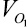
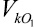 и
и 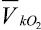 :
:
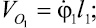
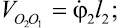
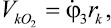
где rk – радиус вектор k-й точки стержня 3 в относительном вращении вокруг полюса O2.
Подставляя эти выражения в формулу для кинетической энергии стержня 3, раскрывая суммы и учитывая что 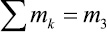 – масса стержня 3,
– масса стержня 3, 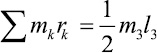 – статический момент стержня 3 относительно точки O2,
– статический момент стержня 3 относительно точки O2, 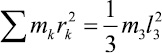 – момент инерции стержня 3 относительно точки O2, окончательно для кинетической энергии стержня 3 получим выражение
– момент инерции стержня 3 относительно точки O2, окончательно для кинетической энергии стержня 3 получим выражение
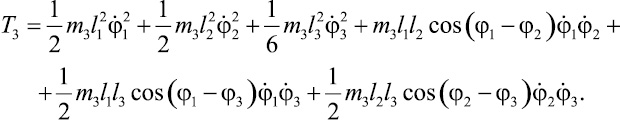 (7)
(7)
Подставляя (3), (4) и (7) в выражение (2) для кинетической энергии системы, получим
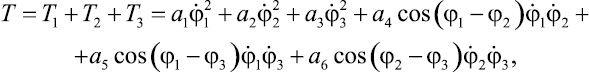 (9)
(9)
где коэффициенты ai, характеризующие инерционные свойства системы, определяются выражениями
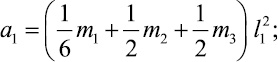
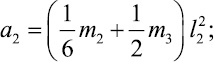
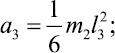
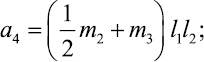
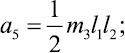
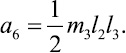
Правые части уравнений Лагранжа представляют собой обобщенные силы [2], определяемые выражением
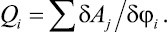
где 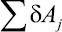 – сумма работ активных сил, действующих на систему на ее возможном перемещении.
– сумма работ активных сил, действующих на систему на ее возможном перемещении.
Учитывая, что на систему действует только момент активных сил M, получим
Q1 = M; Q2 = 0; Q3 = 0. (10)
После определения производных от кинетической энергии системы (9), образующих левые части уравнений Лагранжа, получим дифференциальные уравнения второго порядка:
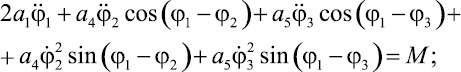 (11)
(11)
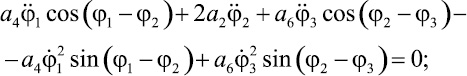 (12)
(12)
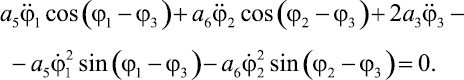 (13)
(13)
Система уравнений (11), (12) и (13) представляет собой математическую модель динамики исследуемой механической системы с тремя степенями свободы.
Представим систему нелинейных дифференциальных уравнений (11), (12) и (13) в виде удобных для практического решения задач:
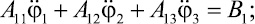 (14)
(14)
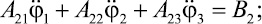 (15)
(15)
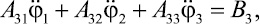 (16)
(16)
где Aij и Bk определяются выражениями
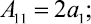
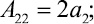
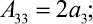
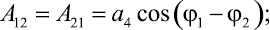
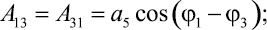
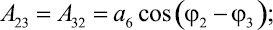
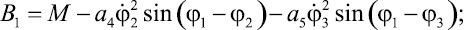
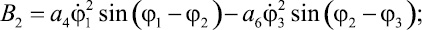
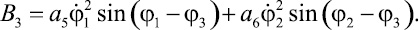
Решение системы уравнений (14), (15) и (16) может быть осуществлено различными численными методами [1, 3].
Рассмотрим результаты решения, полученные при реализации метода Рунге – Кутта четвертого порядка. На рис. 2 представлены зависимости углов поворота стержней φ1, φ2 и φ3 от времени, а на рис. 3 показаны зависимости угловых скоростей 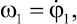
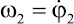 и
и 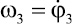 от времени. Представленные зависимости получены при следующих исходных данных и начальных условиях:
от времени. Представленные зависимости получены при следующих исходных данных и начальных условиях:
m1 = m2 = m3 = 1 кг; l1 = l2 = l3 = 1 м;
M = 1 Нм; t = 0;
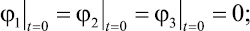
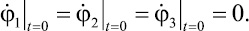
а
б
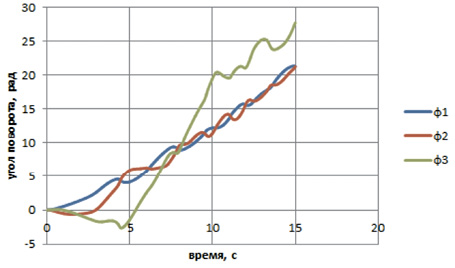
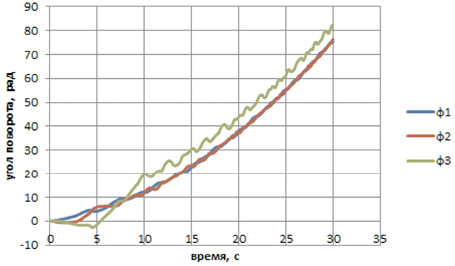
Рис. 2. Зависимость углов поворота стержней от времени:
а – зависимость углов поворота стержней от времени на этапе неустановившегося движения;
б – зависимость углов поворота стержней от времени на этапе установившегося движения
а
б
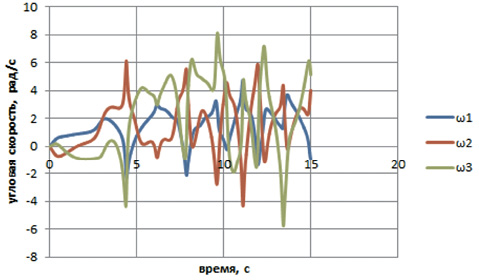
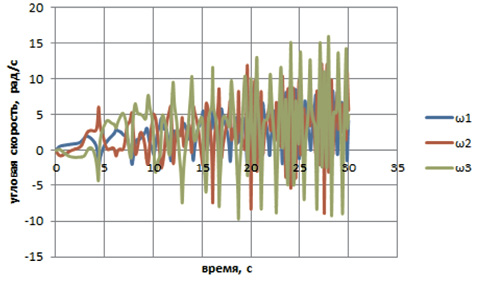
Рис. 3. Зависимость угловых скоростей от времени:
а – зависимость угловых скоростей от времени на этапе неустановившегося движения;
б – зависимость угловых скоростей от времени на этапе установившегося движения
Анализ результатов решения показывает, что движение системы можно разделить на этапы неустановившегося и установившегося движений. На этапе неустановившегося движения стержни 2 и 3 поворачиваются в направлении, противоположном вращению стержня 1 (рис. 2, a и 3, a), после чего меняют направление вращения. Через небольшой промежуток времени (при φ1 ≈ φ2 ≈ φ3 ≈ 2π) можно говорить о начале установившегося движения. Все стержни вращаются в одном направлении, образуя практически прямую линию (рис. 2, б, 3, б). Стержень 3 опережает стержни 1 и 2 на один оборот φ1 ≈ φ2, φ3 ≈ φ1 + 2π.
Заключение
Анализ графиков углов поворота и угловых скоростей на этапе установившегося движения системы показывает, что движение стержней 1, 2 и 3 обладает признаками периодичности. Движение стержней можно рассматривать как сложное, состоящее из переносного и относительного движений. За переносное движение можно принять равноускоренное вращение стержней вокруг неподвижного центра О с равными угловыми скоростями и угловыми ускорениями. В этом случае относительные движения стержней будут представлять собой затухающие колебания с возрастающими частотами.
Результаты решения, полученные при других исходных данных и начальных условиях, позволяют сделать следующие выводы:
– длительность неустановившегося движения зависит от момента активных сил М, при увеличении момента активных сил время неустановившегося движения уменьшается;
– минимальное значение углов поворота второго и третьего стержней не зависит от величины момента активных сил, а зависит только от начальных условий.
Результаты работы могут быть использованы для разработки математических моделей динамики незамкнутых кинематических цепей.
Рецензенты:
Панов А.Ю., д.т.н., заведующий кафедрой «Теоретическая и прикладная механика», ФГБОУ ВПО «Нижегородский государственный технический университет»,
г. Нижний Новгород;
Кретинин О.В., д.т.н., профессор кафедры «Автоматизация машиностроения», ФГБОУ ВПО «Нижегородский государственный технический университет», г. Нижний Новгород.
Работа поступила в редакцию 28.11.2014.



