Для расчета нестационарной концентрации солей в трещине произвольного сечения автором предлагается приближенный метод, основанный на совместном применении интегральных преобразований и вариационных методов.
Предположим, что ось и образующая трещины перпендикулярны к плоскости х, у, т.е. совпадают с направлением оси z. В сечениях, параллельных плоскости х, у, тело имеет постоянную геометрическую форму области D. Обозначим через Г границу области D, тогда Г служит направляющей цилиндрического тела. В частности, если границей области D будет окружность, то получаем обычный круговой цилиндр.
Пусть замкнутая кривая Г аналитически выражается уравнением
F(x, y) = 0. (1)
В этом случае задача нестационарной концентрации при переменных коэффициентах записывается в следующем виде:
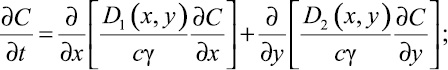 (2)
(2)
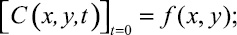 (3)
(3)
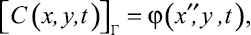 (4)
(4)
где x′, y′ – координаты точки на кривой Г;
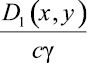 – коэффициент диффузии вещества, м2/с. Применим к уравнению (2) и граничным условиям (4) преобразование Лапласа, тогда
– коэффициент диффузии вещества, м2/с. Применим к уравнению (2) и граничным условиям (4) преобразование Лапласа, тогда
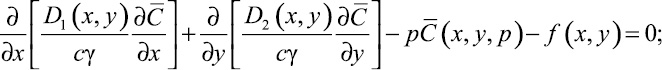 (5)
(5)
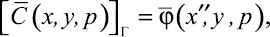 (6)
(6)
где 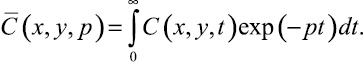
При этом мы предположили, что замена порядка интегрирования по времени t и дифференцирования по времени x, y оправдана.
Пусть
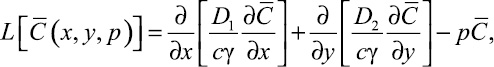 (7)
(7)
тогда уравнение (5) принимает вид
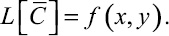 (8)
(8)
Определим функцию 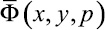 , непрерывную и дифференцируемую до второго порядка в области D, которая на границе Г удовлетворяет условиям (5). Далее введем вспомогательную функцию
, непрерывную и дифференцируемую до второго порядка в области D, которая на границе Г удовлетворяет условиям (5). Далее введем вспомогательную функцию 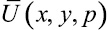 , определяемую равенством
, определяемую равенством
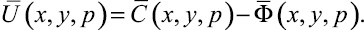 (9)
(9)
Для функции 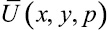 из уравнения (5) и условия (4) получаем
из уравнения (5) и условия (4) получаем
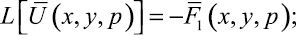 (10)
(10)
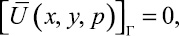 (11)
(11)
где
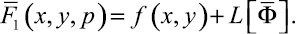 (12)
(12)
Для определения приближенного значения функции 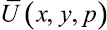 граничной задачи (10), (11) можно применить один из вариационных методов – метод Бубнова – Галеркина [4]. Пусть нами выбрана система координатных функций
граничной задачи (10), (11) можно применить один из вариационных методов – метод Бубнова – Галеркина [4]. Пусть нами выбрана система координатных функций
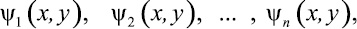 (13)
(13)
которая удовлетворяет нулевым граничным условиям (12), т.е.
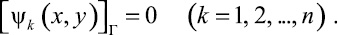
Приближенное решение граничной задачи (10), (11) будем искать в семействе функций вида
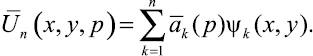 (14)
(14)
Для уравнения (10) составим невязку при 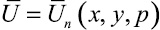 :
:
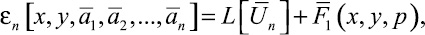 (15)
(15)
которая, вообще говоря, отлична от нуля в области D (в противном случае 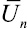 будет точным решением граничной задачи). Для определения коэффициентов
будет точным решением граничной задачи). Для определения коэффициентов 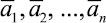
при которых невязка εn наименее уклонялась бы от нуля, следуя методу Бубнова –Галеркина, потребуем ортогональность невязки ко всем координатным функ-
циям (13) [4]:
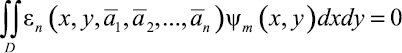 (16)
(16)
или
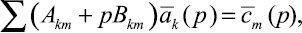 (17)
(17)
где 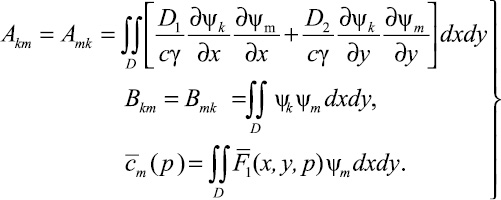 (18)
(18)
Можно показать, что система (17) единственным образом определяет коэффициенты 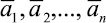 , когда координатные функции (13) линейно независимые [5].
, когда координатные функции (13) линейно независимые [5].
Пусть эти коэффициенты найдены, тогда в области оригиналов решение (14) запишется в форме
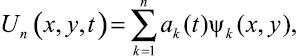 (19)
(19)
где 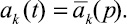 Приближенное поле концентрации исходной краевой задачи запишется формулой
Приближенное поле концентрации исходной краевой задачи запишется формулой
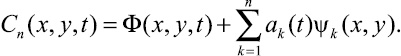 (20)
(20)
В этом заключается метод совместного применения интегрального преобразования и вариационного исчисления к задачам с переменными коэффициентами.
Остановимся на методе подбора системы координатных функций ψk(x, y) (k = 1, 2, ..., n). В качестве функций ψk(x, y) можно брать различные комбинации тригонометрических функций или полиномов. При таком выборе системы координатных функций доказывается полнота системы (13) и сходимость приближенного решения к точному [4].
Пусть нами подобрана функция
ψ0(x, y) > 0, непрерывная внутри области D и равная нулю на границе Г. Тогда в качестве основной системы координатных функций можно принять:
ψ1(x, y) = ψ0(x, y);
ψ2(x, y) = ψ0(x, y)x;
ψ3(x, y) = ψ0(x, y)y; ..., (21)
таким образом, выбор системы координатных функций сводится по существу к определению функции ψ0(x, y). Для улучшения сходимости приближенных решений предлагаем выбор функции ψ0(x, y) связать с геометрической формой (уравнением) границы области D. Так, например, для прямоугольника [–a ≤ x ≤ a, –b ≤ y ≤ b] следует брать
ψ0(x, y) = (a2 – x2)(b2 – y2) > 0.
Для окружности с центром в начале координат (x2 + y2 = R2):
ψ0(x, y) = R2 – x2 + y2 > 0.
Если уравнение кривой Г имеет вид
F(x, y) = 0, то
ψ0(x, y) = ±F(x, y) > 0.
Ниже будут рассмотрены задачи нестационарной концентрации цилиндрических тел с прямоугольным, треугольным и параболическим сечениями при постоянных коэффициентах [1–3].
1. Пусть областью D является часть плоскости x, y, ограниченная линиями x = 0, y = 0, x = l, y = b. Приближенное решение (20) граничной задачи (10), (12) в области оригиналов запишется в данном случае так:
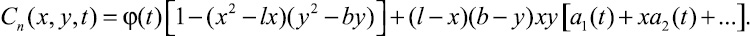 (22)
(22)
Определим решение в первом приближении, когда
φ(x′, y′, t) = 0
и
f(x, y) = C0 = const.
Из системы (17) при n = 1 получим
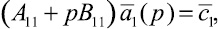
где
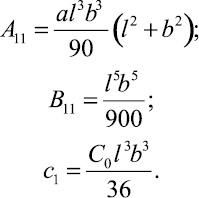
Следовательно,
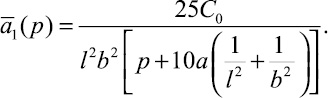
Относительное поле концентрации в первом приближении запишется формулой
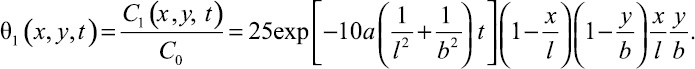 (23)
(23)
Дальнейшие вычисления коэффициентов 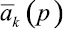 показывают, что решения во втором и третьем приближениях совпадают с первым.
показывают, что решения во втором и третьем приближениях совпадают с первым.
Пусть l = b = 2c (квадратная трещина), тогда
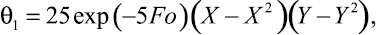 (24)
(24)
где 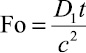 – критерий Фурье;
– критерий Фурье; 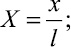
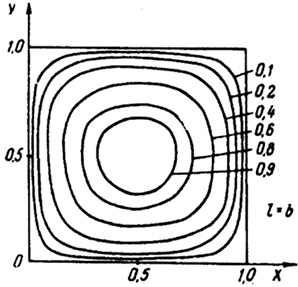
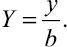 Из формул (23), (24) легко построить поверхности изоконцентрации внутри тела (прямоугольный, рис. 1, а и квадратный, рис. 1, б) для любого момента времени.
Из формул (23), (24) легко построить поверхности изоконцентрации внутри тела (прямоугольный, рис. 1, а и квадратный, рис. 1, б) для любого момента времени.
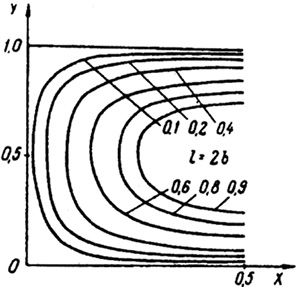
а б
Рис. 1. Поверхности изоконцентрации при q = 0,1; 0,2; 0,4; 0,6; 0,8 и Fo = 0,08
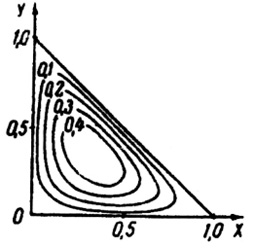
а б
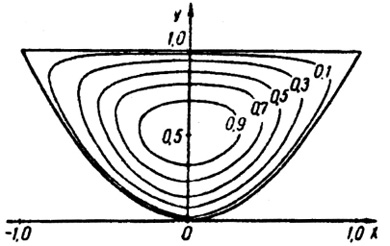
Рис. 2. Поверхности изоконцентрации внутри трехгранного тела и цилиндрического тела с параболическим сечением при Fo = 0,08, рассчитанные по формулам (26), (29)
2. Пусть областью D (рис. 2, а) является треугольник со сторонами x = 0, y = 0, x + y = l.
Решение исходной задачи для случая φ(x′, y′, t) = 0 и f(x, y) = C0 = const в первом приближении принимает вид
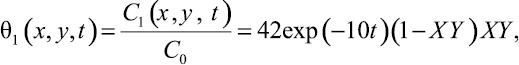 (25)
(25)
где 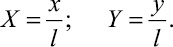
Полагая l = 2c, получаем
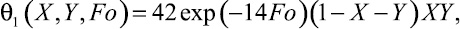 (26)
(26)
где
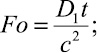 0 ≤ θ1 ≤ 1.
0 ≤ θ1 ≤ 1.
Сравнивая формулы (26) с формулой (24), можно отметить, что темп растворения трехгранного тела (exp(–14Fo)) значительно выше, чем у квадратного (exp(–5Fo)). Это объясняется тем, что при равной концентрации количество аккумулированного вещества в первом теле в два раза меньше, чем во втором. В то же время поверхности концентрации на 1 пог. м для этих тел соответственно равны 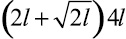 , т.е., несмотря на то, что объем первого тела в два раза меньше, чем у второго, их поверхности концентрации почти равны между собой.
, т.е., несмотря на то, что объем первого тела в два раза меньше, чем у второго, их поверхности концентрации почти равны между собой.
3. Цилиндрическое тело с параболическим перпендикулярным сечением. Пусть область D (рис. 2, б) ограничена линиями y = kx2 и y = h (–b ≤ x ≤ b, 0 ≤ y ≤ h). Приближенное решение краевой задачи, когда на границе поддерживается нулевая концентрация, в области изображений ищем в виде
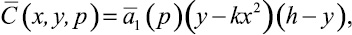 (27)
(27)
где
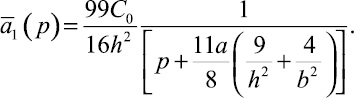
Поле концентрации внутри цилиндрического тела с параболическим сечением в первом приближении запишется следующей формулой:
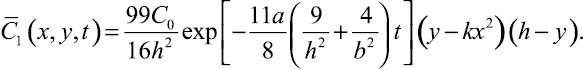 (28)
(28)
Положим а = 1, b = 1, h = 2c, тогда из (28) получим
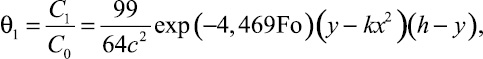
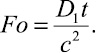 (29)
(29)
Следовательно, предложенный метод дает возможность решить задачи нестационарного поля концентраций для цилиндрических тел с другими «неклассическими» профилями перпендикулярного сечения.
Рецензенты:Агаханов Э.К., д.т.н., профессор, зав. кафедрой «Автомобильные дороги, основания и фундаменты», ФГБОУ ВПО «Дагестанский государственный технический университет», г. Махачкала;
Рамазанов А.-Р.К., д.ф.-м.н., профессор, заведующий кафедрой математического анализа, Фгбоу ВПО «Дагестанский государственный университет», г. Махачкала.
Работа поступила в редакцию 02.12.2014.



