Постановка задачи. Для инерционных приборов устанавливается связь между функциональными характеристиками (ускорением, скоростью прибора и временем движения чувствительного элемента для коммутирования тока в электрических цепях) и конструктивными параметрами прибора. С использованием [1, 2] применяется теорема об изменении кинетической энергии в подвижной системе отсчета. Классификация инерционных приборов выполнена по характеру движения чувствительного элемента: поступательное, вращательное. Выполнен системный анализ влияния конструктивных параметров и закона изменения переносного ускорения (одно из наиболее важных внешних воздействий) на функциональные характеристики прибора (время движения чувствительного элемента). Принципиально новыми инструментами при использовании математического моделирования являются концептуальная модель прибора и причинно-следственная диаграмма. Концептуальная модель прибора служит для формирования множества системных показателей и алгоритмов их вычисления, причинно-следственная диаграмма – для установления параметров прибора и технологических процессов, влияющих на функциональные характеристики прибора.
Концептуальная модель инерционного прибора выполнена на рис. 2.
На рис. 3 показана причинно-следственная диаграмма оценки факторов, влияющих на функциональные характеристики инерционного прибора [6].
Для определения времени срабатывания прибора применена теорема об изменении кинетической энергии в относительном движении по отношению к неинерциальной системе отсчета:
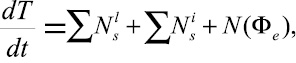 (1)
(1)
где Т – кинетическая энергия системы; N – мощность внешних, внутренних сил и переносных сил инерции. С учетом того, что в систему входят абсолютно твердые тела, мощность внутренних сил равна нулю, 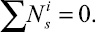
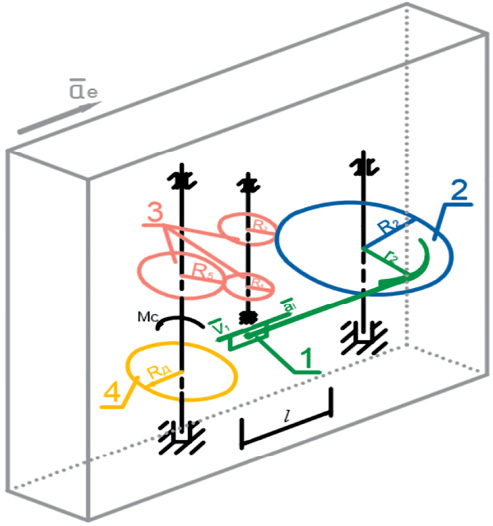
Рис. 1. Кинематическая схема инерционного прибора:
1 – чувствительный элемент; 2 – зубчатый сектор; 3 – зубчатая передача;
4 – диск магнитного тормоза
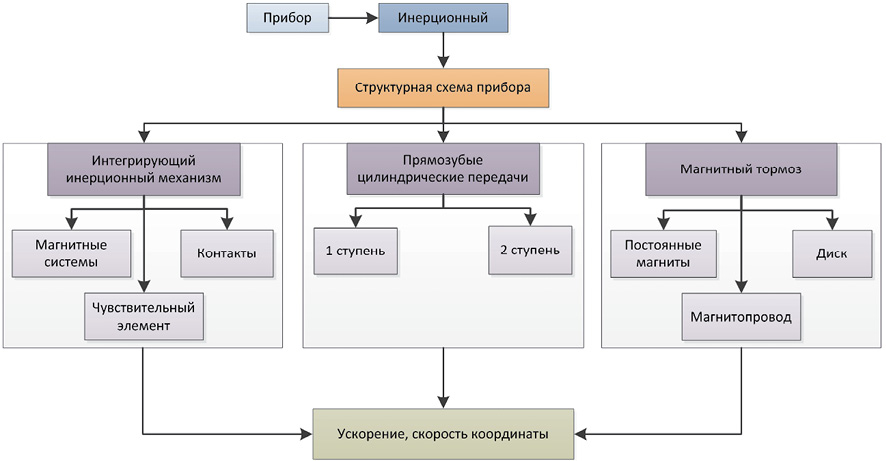
Рис. 2. Концептуальная модель инерционного прибора
Кинетическая энергия системы, выраженная через скорость чувствительного элемента:
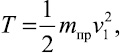 (2)
(2)
где mпр – приведенная масса системы с одной степенью свободы.
Мощность внешних сил и переносных сил инерции:
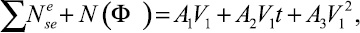 (3)
(3)
где А1, А2, А3 – коэффициенты, определяемые для рассматриваемого прибора.
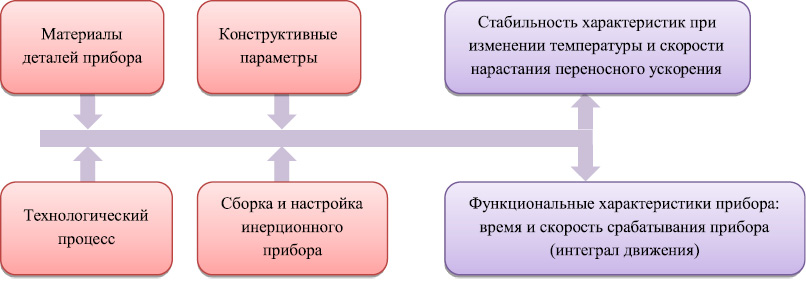
Рис. 3. Причинно-следственная диаграмма для инерционного прибора
Закон движения чувствительного элемента при заданных начальных условиях:
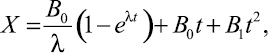 (4)
(4)
где λ – один из корней характеристического уравнения.
Зная расстояние l (рис. 1), определяем время срабатывания и скорость прибора (интеграл движения).
С учетом (4) построены зависимости времени срабатывания прибора от конструктивных параметров (в частности, шероховатости поверхности) и коэффициента нарастания ускорения. Зависимость времени срабатывания от шероховатости поверхности позволяет установить параметры технологического процесса, определяющие критичные параметры прибора и его функциональные характеристики. При этом расчет выполняется в следующей последовательности. На основе экспериментальных соотношений установлена зависимость шероховатости поверхности от параметров операционной технологии (скорости резания, глубины, подачи). С использованием литературных данных построена зависимость коэффициента трения от шероховатости материала. Знание аналитических зависимостей времени срабатывания от коэффициента трения позволяет установить границы параметров операционной технологии, обеспечивающие требуемые функциональные характеристики.
Знание зависимости времени срабатывания от закона нарастания ускорения при определенных конструктивных параметрах позволяет решить основную проблему функционирования инерционного прибора – обеспечить постоянство скорости движения подвижной системы отсчета (скорости срабатывания) при различных законах изменения переносного ускорения.
Отметим, что наибольший интерес полученные результаты, в частности (4), представляют для решения задачи синтеза конструктивных параметров прибора, причем количественные результаты согласуются с данными [3, 4].
Инерционный прибор с чувствительным элементом, совершающим
вращательное движение
На рис. 4 показана часть инерционного прибора, когда положение чувствительного элемента определяется угловой координатой ϕ. При определении функциональных характеристик прибора учтены следующие факторы:
а) закон изменения переносного ускорения;
б) значения нагрузок на чувствительный элемент прибора, определяемых его регулирующими системами (с учетом различных вариантов регулировок и настроек магнитных систем);
в) допуски на геометрические размеры деталей и шероховатость поверхностей;
г) отклонения магнитных свойств материалов, применяемых в регулировочных устройствах.
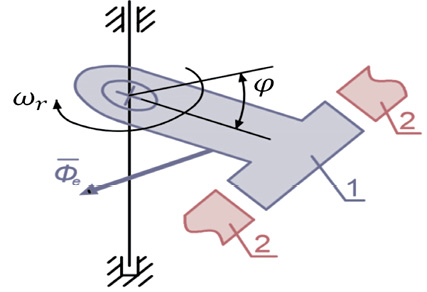
Рис. 4. Элемент инерционного
интегрирующего прибора:
1 – чувствительный элемент;
2 – магнитные устройства регулирования; Φе – равнодействующая сил инерции для чувствительного элемента
Расчет интегрирующего прибора разделен на два режима – условие равновесия и условие движения чувствительного элемента. Для каждого режима работы составлены расчетные схемы в неинерциальной системе отсчета. Движение чувствительного элемента разделено на секторы, в каждом из которых на него действуют моменты внешних сил, моменты регулирующих устройств, сил трения, моменты сил инерции. Расчет силовых характеристик регулирующих систем выполнен с помощью пакетов ANSYS, Pro/Engineer с последующей аппроксимацией.
Структура дифференциального уравнения движения чувствительного элемента по каждому из участков
имеет вид
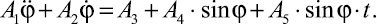 (5)
(5)
Полученные уравнения являются нелинейными, поэтому их решение выполнено численным методом, интегрированным в программу Mathematica [5].
В результате решения уравнений во всех секторах получаем время срабатывания прибора и, соответственно, скорость его срабатывания:
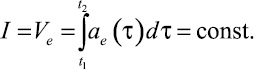 (6)
(6)
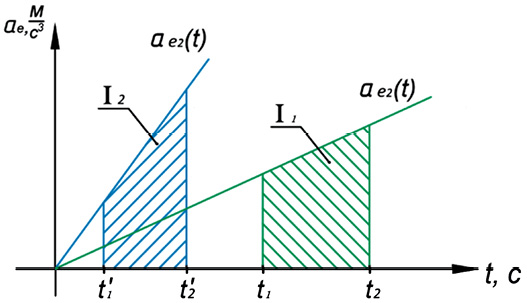
Рис. 5. Скорость срабатывания прибора для двух законов нарастания ускорения
На рис. 5 показано постоянство скорости срабатывания прибора для реальных конструктивных параметров прибора при различных законах изменения переносного ускорения.
Заключение
1. Разработана математическая модель инерционного прибора, позволяющая оценить влияние конструктивных параметров прибора на время срабатывания.
2. Установлено, что наиболее существенное влияние оказывают напряженность магнитного поля с учетом зазоров в регулирующих устройствах и коэффициент торможения магнитного тормоза.
Рецензенты:Паршин В.С., д.т.н., профессор, заведующий кафедрой «Металлургические и роторные машины» механико-машиностроительного института, Уральский федеральный университет им. первого Президента России Б.Н. Ельцина, г. Екатеринбург;
Чечулин Ю.Б., д.т.н., профессор кафедры «Детали машин» механико-машиностроительного института, Уральский федеральный университет им. первого Президента России Б.Н. Ельцина, г. Екатеринбург.
Работа поступила в редакцию 28.11.2014.



