Прогнозирование поведения материалов при выполнении технологических операций в различных режимах взаимодействия с обрабатывающей средой особенно необходимо, когда лабораторные и производственные методы испытаний затруднены или практически невозможны. В этих случаях для решения технологических задач предпочтительным, а иногда единственно возможным является использование модельных методов исследования и расчёта режимов обработки.
Это обстоятельство становится особенно важным в условиях производства и эксплуатации швейных изделий из легкодеформируемых композитных материалов, которые при воздействии внешней среды в процессе их изготовления и эксплуатации испытывают разнонаправленные деформации.
Целью исследований является анализ возможностей использования механических аналогов для формализации процесса релаксации напряжения при постоянной деформации материала применительно к легкодеформируемым волокнистым композитам.
Материал и методы исследований
Объектом исследований являются легкодеформируемые волокнистые материалы (ЛДВМ), а их предметом – моделирование процесса релаксации ЛДВМ при постоянной деформации. При проведении исследований использовались аналитические методы, базирующиеся на использовании механических аналогов, в сочетании с экспериментальными подходами.
Результаты исследования и их обсуждение
Деформационно-релаксационный характер поведения легкодеформируемых материалов при действии внешних механических сил значимо отражается на качестве готовых изделий. Однако эти вопросы далеко не всегда учитываются в практике проектирования и выборе пакета материалов на изделие. Причиной тому являются недостаточные исследования механизма деформационно-релаксационных процессов, протекающих в структуре материалов и конструктивно-технологических блоках изделий при выполнении технологических операций. Для формализации процесса релаксации напряжения при постоянной деформации материала в той или иной степени могут быть использованы аналитические методы, базирующиеся на использовании механических аналогов, в сочетании с экспериментальными подходами [1–6, 8].
Одним из ключевых вопросов исследования напряжённо-деформированного состояния (НДС) легкодеформируемых композитных материалов является возможность определения посредством расчёта продолжительности процесса формования изделий для придания им устойчивой пространственной формы при выполнении операции влажно-тепловой обработки и обеспечения ее устойчивости при эксплуатации [2, 7]
Вследствие нелинейности процесса релаксации напряжения композитных материалов для условий постоянной деформации в работе в качестве базовой принята механическая модель Фойгта – Кельвина, математическое отображение которой имеет вид [1]
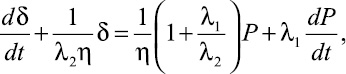(1)
где λ1 и λ2 – податливости упругих элементов; h – вязкость демпфера; Р – сила нагружения.
В качестве одного из упругих элементов этой модели для приближения к реальному процессу релаксации напряжения при постоянной деформации в задачу аналитических исследований введём негуковское звено Лидермана [5] (рис. 1).
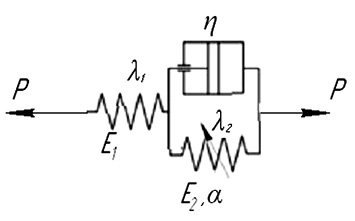
Рис. 1. Трёхпараметрическая модель Фойгта – Кельвина – Лидермана
В этом варианте деформация (ε2) негуковского звена моделируется в контексте релаксации напряжённо-деформированного состояния исследуемой части тела с некоторым переменным коэффициентом a = φ(σ) условного модуля упругости E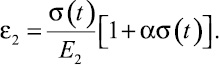2.
(2)
Переходя к использованию негуковского элемента Лидермана в механической модели Фойгта – Кельвина с учетом (2) при одноосном нагружении, будем иметь
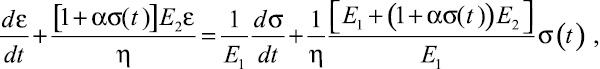(3)
где e – приведенная деформация модели материала; E1 и E2 – соответственно условные модули упругости элементов рассматриваемой механической модели; σ(t) – текущее напряжение элементов модели вследствие релаксации силового взаимодействия.
При завершении процесса релаксации усилия после формования изделия при влажно-тепловой обработке (ВТО) значение приведенной деформации e исследуемого тела принимает установившееся фиксированное значение, т.е.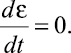 
Исходя из этого и с учётом принятых допущений после выполнения преобразования (1), получим
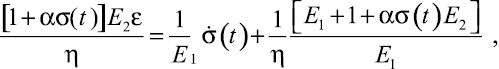(4)
где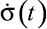 
– производная от параметра σ.
Решая уравнение (4) относительно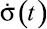 
, получим
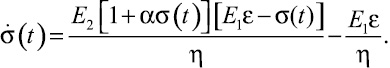(5)
Для удобства аналитического исследования модели введём условные константы реологических свойств элементов композитного материала:
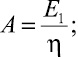
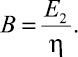(6)
Тогда выражение (5) примет вид
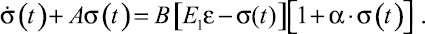(7)
Проведя дополнительные преобразования уравнения (7), что принципиально важно для расчетов, получим в символьной форме функцию a = j(σ):
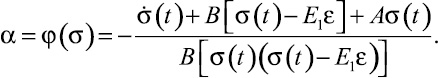(8)
Полученная функция a = j(σ) представляет собой трансцендентное уравнение, которое может быть решено численными методами, но только в случае, если для материала известна функция релаксации напряжения при фиксированной деформации σ(t). Для приведения коэффициентов А и В к известным реологическим свойствам [2], введя в анализ постоянную времени процесса (параметр TR), воспользуемся соотношениями (6).
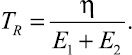(9)
Приведённый показатель упругости рассматриваемого тела механической модели композитного материала будет иметь вид
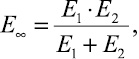(10)
где с учётом (6) получим
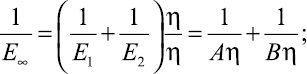(11)
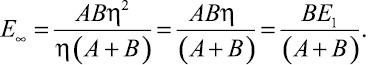(12)
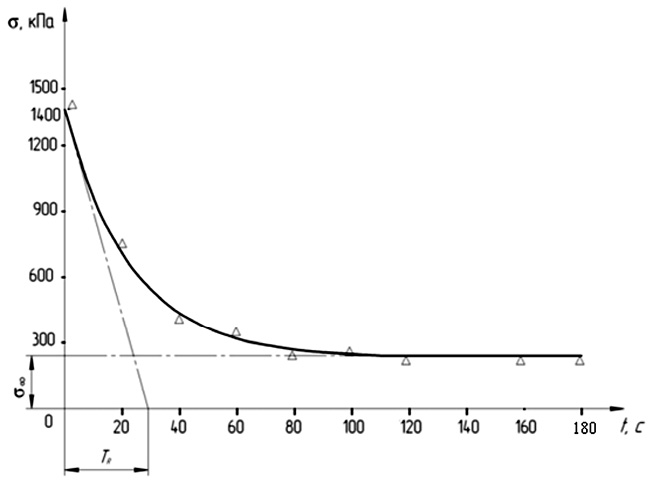
Рис. 2. Экспериментальные результаты релаксации напряжения при влажно-тепловой обработке 120 °С и фиксированной деформации (вид материала: ткань костюмная; волокнистый состав: шерсть 57 %, полиэфир 43 %)
Решая систему уравнений (11) и (12), получим расчётные значения постоянных А и В.
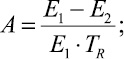
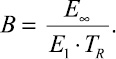
Исходные реологические свойства для конкретного типа композитного материала можно определить экспериментальным путем. Проведенные на базе стенда [7] экспериментальные исследования для костюмной ткани (волокнистый состав: 57 % шерсть; 43 % полиэфир) и полученные фрагменты результатов (рис. 2) позволяют определить искомые параметры:
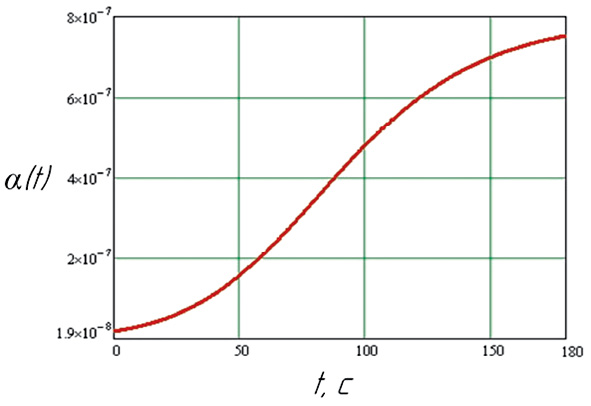
Рис. 3. Изменение коэффициента a = φ(t) условного модуля упругости
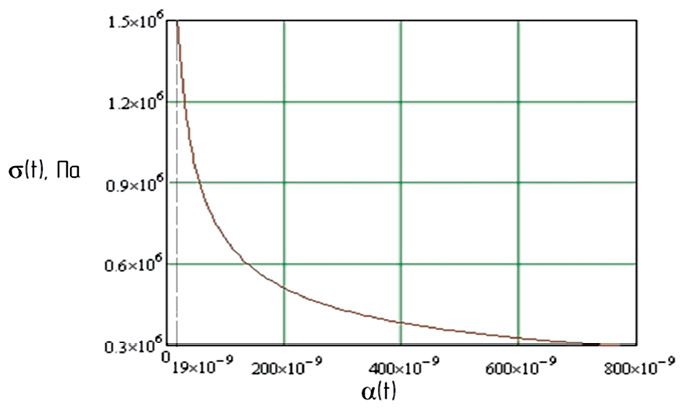
Рис. 4. Расчётная зависимость коэффициента α = f(σ) условного модуля упругости от релаксации напряжения при постоянной деформации
Таким образом, экспериментально определенная для рассматриваемой ткани функция релаксации напряжения при фиксированной деформации σ(t) в виде эмпирической формулы имеет вид
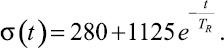
На базе полученных данных с использованием пакета программ MhatCad14 определены численные значения функций α = f(σ), a = φ(t) и построены соответствующие графические зависимости (рис. 3; 4), позволяющие установить требуемые параметры технологической обработки, прежде всего продолжительность процесса ВТО при формовании деталей изделий.
Заключение
Таким образом, при моделировании процесса релаксации ЛДВМ при фиксированной деформации показано, что расчётные значения коэффициента изменения модуля упругости оказывают влияние на него лишь в начальный период времени, когда действуют максимальные напряжения, а в ходе процесса релаксации усилия значение α = f(σ) стремится к нулевому значению, т.е. a = f(σ) → 0. При этом установлено, что для расчёта кинетики процесса релаксации напряжения при фиксированной деформации и оценки остаточного напряжения легкодеформируемых композитных материалов при их обработке в тепловом поле с определёнными допущениями можно пользоваться аналитикой на базе механической модели Фойгта – Кельвина [2].
Рецензенты:Мансуров Ю.Н., д.т.н., профессор, заведующий кафедрой «Материаловедение и технология материалов» Инженерной школы, профессор кафедры «Инноватика, качество, стандартизация и сертификация», Дальневосточный федеральный университет, г. Владивосток;
Бойцова Т.М., д.т.н., профессор, директор института сервиса, туризма и дизайна, ФГБОУ ВПО «Владивостокский государственный университет экономики и сервиса» Минобрнауки РФ, г. Владивосток.
Работа поступила в редакцию 28.11.2014.