Проведение анализа многих современных объектов, связанных с рассеянием электромагнитных волн, демонстрирует, что в них для большинства случаев используется сложная структура. Осуществление процессов анализа и синтеза подобных структур требуется вести с применением моделей и методов, которые дают весьма небольшие ошибки.
При получении информации о различных объектах, работающих в радиолокационном диапазоне на основе осуществления как натурных, так и физических экспериментов, может потребоваться привлечение значительных материальных, организационных и временных затрат. В этой связи как одни из наиболее доступных способов для получения соответствующей информации о том, какие характеристики рассеяния у объектов, могут быть рассмотрены методы математического моделирования.
На основе применения классических асимптотических методов высокочастотной дифракции не всегда есть возможность без сложного обобщения и усовершенствования проводить расчет для характеристик рассеяния при учете многих факторов, например, таких как как степень сложности поверхности объектов, размещение разных материалов на поверхности объекта, которые поглощают радиоизлучение. Их могут помещать также и на разных изломах поверхности, проводить анализ при существовании подстилающих поверхностей, осуществлять разнесенный прием.
Исходя из вышесказанного изучение характеристик рассеяния различных технических объектов определяет необходимость развития методов оценки уровней электромагнитного рассеяния.
Проведение расчета характеристик рассеяния объектов, имеющих сложную форму, ведет к необходимости проведения подробного математического описания особенностей его поверхности.
Среди основных методов моделирования поверхностей объекта следует отметить:
1. Метод тел вращения.
2. Способы проведения аналитического описания поверхностей.
3. Подходы, использующие простейшие компоненты.
4. Представление объекта на основе проволочных моделей.
5. Способы, использующие аппроксимацию поверхностей объекта на основе элементарных участков.
Во многих случаях при проведении исследований и проектировании сложных электродинамических объектов применяют системы автоматизированного проектирования (САПР). Это позволяет значительно расширить класс объектов, для которых ставятся и решаются разные задачи, связанные с рассеянием электромагнитных волн (ЭМВ) [4, 5, 8].
При проведении решения задач дифракции радиоволн и проектировании соответствующих технических объектов для многих случаев рассматривают структуры, имеющие на своей поверхности материалы, которые поглощают электромагнитное излучение [9].
Проведение расчета характеристик рассеяния для объектов сложной формы во многих случаях сталкивается с серьезными математическими, а также вычислительными трудностями. В этой связи с точки зрения практики часто привлекают асимптотические методы дифракции.
При этом в качестве основы выбирают метод краевых волн. Но для описания различных геометрооптических секторов в условиях разнесенного приема, наличия покрытий, поглощающих радиоизлучение, требуется модификация этого метода.
С другой стороны, можно использовать метод интегральных уравнений.
В данной статье мы рассматриваем двумерную модель рассеяния электромагнитных волн. Это обусловлено тем, что трехмерные задачи можно решать для определенных условий при двумерном приближении.
Цель данной работы состоит в исследовании характеристик рассеяния электромагнитных волн на полых структурах с поглощающими покрытиями и разработка предложений по структуре подсистемы САПР для проектирования соответствующих объектов.
Методика. Рассмотрим рассеяние ЭМВ на двумерной полой структуре, которая на своей внутренней поверхности имеет поглощающее покрытие с постоянной толщиной (рис. 1).
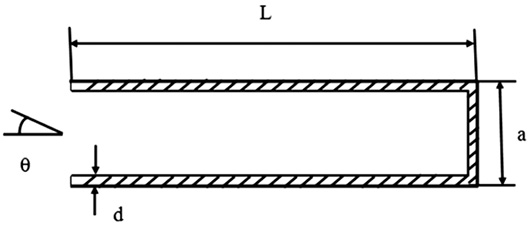
Рис. 1. Геометрия рассеяния ЭМВ на двумерной полой структуре с поглощающим покрытием, здесь a, L – размеры полой структуры, d – толщина поглощающего покрытия, q – угол падения плоской ЭМВ
Полагаем, что электрическое поле (случай E-поляризации) для произвольной точки наблюдения E(x0, y0). При этом точку (x0, y0) мы размещаем в сечении S поглощающего покрытия, а также на контур металла. При этом на основе использования граничных условий возникает система интегральных уравнений. Это уравнения Фредгольма 1-го рода [7].
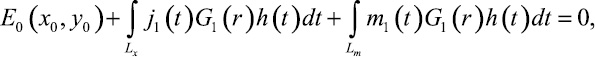для (x0, y0) ∈ Lx;
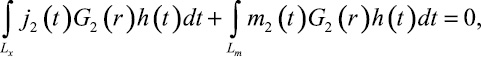для (x0, y0) ∈ Lx;
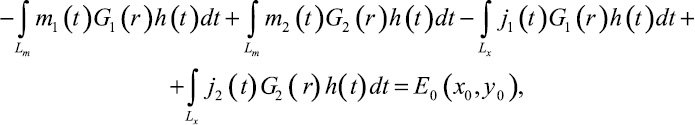для (x0, y0) ∈ Lm;
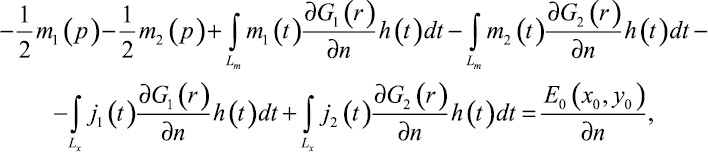для (x0, y0) ∈ Lm.
Здесь j1, m1 – представляют собой плотности потенциалов для внешних сторон контуров Lx (металл) и Lm (поглощающее покрытие) соответственно; j2, m2 – обозначают значения плотностей потенциалов по внутренним сторонам контуров, E0(x0, y0) – падающая плоская электромагнитная волна, q – угол падения и наблюдения волны (рис. 1), G1(r) – представляет собой двумерную функцию Грина, соответствующую бесконечной области, которая имеет волновое число k = 2p/l, l – соответствует длине волны в области свободного пространства, G2(r) – обозначает двумерную функцию Грина, соответствующей бесконечной области, имеющей волновое число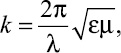 
r – расстояние между исходной точкой и точкой наблюдения, h – определяет коэффициент Ламе по контуру L.
Задачу, связанную с решением систем интегральных уравнений Фредгольма первого рода, можно отнести к классу некорректных задач.
При решении указанной электродинамической задачи можно выделить несколько основных этапов.
1. Получают математические соотношения среди интересующих нас физических величин.
2. Вводятся определенные ограничения на то, какое поведение у полей и источников для подлежащих анализу.
3. Получают численные результаты. Для решения указанной задачи мы будем применять метод моментов.
Анализ показывает, что выделяют два типа систем базисных функций.
Для использования метода привлекают базис полной области и базисы подобласти.
Довольно эффективно применение систем базисных функций, относящихся к полным областям для случаев, когда наблюдается гладкое решение задачи.
Базисные функции во многих случаях строятся с привлечением разложения анализируемой функции в двумерный ряд Фурье, поскольку в этом случае наблюдается близость базиса с точки зрения формы к тому результату, который мы ожидаем. Это ведет к тому, что заметным образом происходит снижение порядка матрицы импедансов, которая получается при осуществлении дискретизации интегральных уравнений.
Рассеянное электромагнитное поле рассчитывалось на основе соответствующих формул [1, 3].
Проводились расчеты ЭПР полой структуры на основе рассмотренного подхода. На рис. 2 приведены пример результата расчета эффективной поверхности рассеяния (ЭПР) при изменении толщины покрытия d для угла наблюдения q = 0°. Размеры были следующими: L = 3,1l, L = 3,1l. Значение диэлектрической проницаемости покрытия было такое 13-j⋅17.
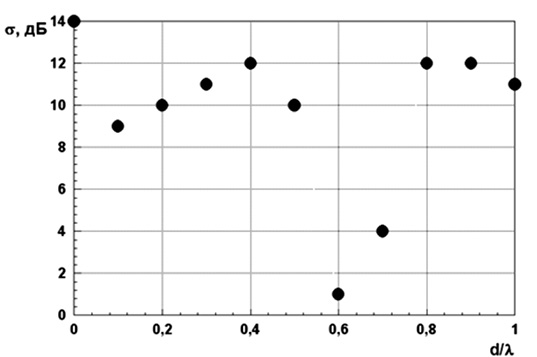
Рис. 2. Пример зависимости ЭПР от толщины покрытия
Таким образом, полученные зависимости значений ЭПР от толщин различных покрытий могут храниться в БД и далее передаваться в подсистему САПР для построения объектов с заданными характеристиками.
Описание особенностей подсистемы САПР
В полой структуре выделяют модуль для расчета характеристик металлического объекта и модуль для расчета характеристик покрытия. Проводится оптимизация значений амплитуд рассеян ного поля [2, 6].
На рис. 3 приведена схема подсистемы САПР для определения требуемых характеристик полой структуры
В качестве выходных результатов мы рассматриваем значения характеристик полых структур, входящих в состав технического объекта.
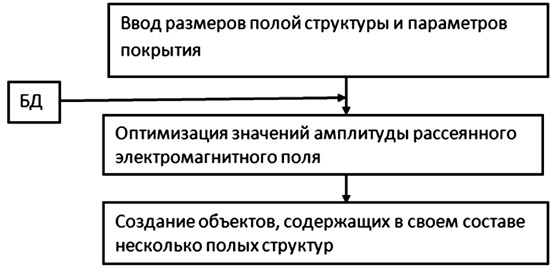
Рис. 3. Процесс функционирования подсистемы САПР средних характеристик объекта
Заключение
Таким образом, приведенный в статье подход и результаты анализа говорят о том, что предлагаемая подсистема будет полезна при проведении проектирования объектов, содержащих полые структуры, содержащие покрытия.
Рецензенты:Кострова В.Н., д.т.н., профессор, проректор по мониторингу Воронежского института высоких технологий, г. Воронеж;
Чопоров О.Н., д.т.н., профессор, проректор по научной работе Воронежского института высоких технологий, г. Воронеж.
Работа поступила в редакцию 18.11.2014.