Изучением процессов распределения воды и грязи по кузову автомобилей занялись еще в 60-х годах. Скорость автомобилей увеличивалась, поэтому для улучшения видимости и повышения безопасности в целом этот вопрос был и остаётся острым. До недавнего времени ключевым инструментом для изучения обтекаемости автомобиля являлась аэродинамическая труба [5, 14]. Для визуализации потоков используют водяные взвеси с флуоресцентным порошком или красящими частицами. После этого проводится трасологическая экспертиза, которая позволяет выявить распределение грязевых потоков, а также поиск методов борьбы с повышенной загрязняемостью с помощью различных модификаций [15].
Одним из самых простых методов сохранения чистоты боковых стекол является использование навесного оборудования, например молдингов передних стоек, перераспределяющих потоки грязи на крышу, различных канавок на крышах, регулирующих направление стекающей воды на задние стойки, заградительных элементов наружных зеркал [3, 1]. Немаловажным является анализ движения потоков воздуха в подднищевом пространстве автомобиля. Так, в работе [7] представлена математическая модель обтекания днища машины, предложена методика расчета аэродинамического сопротивления. Анализу особенностей формирования пограничного слоя в подднищевой зоне машины и влиянию на подъемную силу и аэродинамическое сопротивление посвящена работа [8]. Влияние расположения кузова относительно дорожного полотна на аэродинамические характеристики изучается в работе [6], где предложено решение задачи уменьшения сопротивления и действующей на автомобиль подъемной силы. Тип шины, рисунок ее протектора, общая конструкция колеса, способ его установки имеет большое влияние на коэффициент сопротивления автомобиля в целом. Детальный анализ движения воздушных потоков проводится не только под днищем, но и внутри колесных шин [4, 10]. Незначительные изменения в конструкции колесной пары или рисунке протектора могут значительно снизить выбросы грязи и воды из-под автомобиля. Каким образом колесо влияет на загрязняемость автомобиля, изучает автор работы [2]. Многие современные машины оснащены дефлекторами, расположенными перед передними колесами, для корректировки аэродинамики днища и уменьшения грязевого шлейфа за транспортным средством. Все модификации автомобиля сопровождаются необходимыми проверками [12], так как каждое изменение конструкции может значительно влиять на возникновение аэродинамических шумов и лобового сопротивления.
С развитием вычислительной техники появилась возможность осуществлять численное моделирование загрязнения автомобиля. Активно разрабатываются алгоритмы и программы по расчёту и оптимизации параметров обтекаемости для доводки автомобиля еще в процессе проектирования [11, 13].
Несмотря на большое количество исследований, вопросы, связанные с загрязнением автомобиля при его движении в колонне, остаются открытыми.
В отличие от вышеописанных исследований, данная работа посвящена исследованию грязевой аэродинамики колонны автомобилей средствами Star CCM+.
В классической постановке задачи [9] об обтекании автомобиля принято рассматривать равномерное прямолинейное движение транспортного средства в привязанной к нему системе координат. Расчёт, как правило, производится в области, имеющей форму прямоугольного параллелепипеда, достаточно большого, чтобы влиянием автомобиля на динамику потоков воздуха на его границах можно было пренебречь.
Для моделирования аэродинамики в более сложных случаях следует рассматривать специфические граничные условия. Так, при движении колонны одинаковых автомобилей с постоянной дистанцией следует рассматривать циклические граничные условия на гранях параллелепипеда, перпендикулярных направлению движения колонны. Длина ребра параллелепипеда, параллельного направлению движения колонны, определяется как сумма длины транспортного средства в движущейся колонне и дистанции. Остальные размеры параллелепипеда определяются так же, как и при решении классической задачи обтекания, исходя из приемлемости вносимой границами погрешности. При использовании такого подхода возможно возникновение некоторой погрешности для первых и последних транспортных средств, движущихся в колонне.
В данной статье приводится описание настройки симуляции и результаты решения задачи загрязнения автомобиля, движущегося в колонне средствами Star CCM+.
Для реализации данной задачи необходимо выполнить несколько этапов. На первом этапе осуществляется численное моделирование обтекания автомобиля, движущегося с заданной скоростью, на основе уравнений Навье – Стокса и k-ε модели турбулентности. После нахождения стационарного решения, на втором этапе осуществляется моделирование движения автомобиля по мокрой дороге с учётом движения частиц воды, выбрасываемых из-под колеса. На этом этапе для моделирования выброса частиц используется модель инжектора, расположенного под задним колесом автомобиля.
Для расчёта аэродинамики и загрязнения необходимо импортировать CAD-модель автомобиля, задать сетку, физические модели и граничные условия. Наиболее нетривиальные граничные условия соответствуют поверхности вращающихся колес. Для их реализации в системе координат, связанной с автомобилем, необходимо задать на их поверхности граничное условие, включающее в себя скорость движения границы. С этой целью определяется угловая скорость вращения через линейную скорость движения автомобиля.
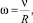 (1)
(1)
где ν – скорость движения автомобиля, м/c; R – радиус колеса, м.
Мгновенная скорость точек на поверхности колеса определяется согласно выражению (2):
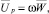 (2)
(2)
где 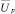 – мгновенная скорость точки на поверхности колеса.
– мгновенная скорость точки на поверхности колеса.
Направление вектора 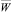 соответствует касательной к данной точке на поверхности колеса с учётом направления движения автомобиля, а его длина равна расстоянию этой точки от оси колеса.
соответствует касательной к данной точке на поверхности колеса с учётом направления движения автомобиля, а его длина равна расстоянию этой точки от оси колеса.
Для реализации в симуляции Star CCM+ граничных условий на колесах, описанных выше, необходимо определение функций поля на основе формул (1)–(2).
После получения стационарного решения задачи обтекания автомобиля следует добавить в симуляцию модель лагранжевой многофазности. Для этого добавляется лагранжева фаза, где задаются частицы материала. В целях упрощения модели частицы грязи моделируются как частицы воды, вылетающие из-под колеса с плотностью, равной 997,561 кг/м3. Выбирается физическая модель, учитывающая взаимное влияние лагранжевой и непрерывных фаз в связи с аэродинамическим сопротивлением, то есть фазы могут обмениваться между собой импульсом. В качестве граничных условий для лагранжевой фазы определяется прилипание, то есть частицы, достигшие поверхности твёрдой фазы, останавливаются, что позволяет выявить наиболее загрязняемые участки на поверхности транспортного средства. Такое граничное условие необходимо для учёта прилипания и дальнейшего анализа процесса загрязнения внешних поверхностей транспортного средства.
В качестве источника подачи частиц воды из-под задних колес используется инжектор в форме конуса, потоком жидких частиц из-под передних колес пренебрегаем. В свойствах учитывается диаметр частиц равный 10–4 м, внешний угол конуса равный 1,7 радиан, согласно эксперименту, проведенному в лаборатории НГТУ, направление расширения конуса противоположно движению автомобиля. Скорость подачи частиц из конуса равна скорости движения автомобиля, а скорость потока массы частиц равна 4 кг/с. Данная величина получена из формулы (3):
 (3)
(3)
где V – скорость потока массы частиц, кг/с; u – скорость движения частиц, м/c; d – ширина колеса, м; l – толщина пленки, мм; ks – коэффициент прилипания; ρ – плотность воды, кг/м3.
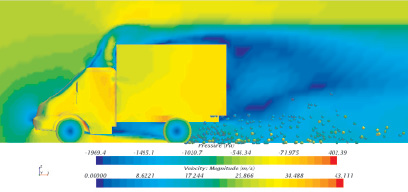
Рис. 1а. Формирование потока частиц из-под колеса (t = 0,397 с)

Рис. 1б. Формирование потока частиц из-под колеса (t = 0,397 с)
Ниже приведены результаты расчета аэродинамики автомобиля, движущегося в колонне по мокрому участку дороги при заданной постоянной скорости 97 км/ч, в программном комплексе Star CCM+. В симуляции предполагалось отсутствие внешних эффектов, таких как встречное движение автомобилей.
Результаты расчётов, полученных на основании данной модели, приведены на рис. 1–2. На всей поверхности автомобиля, за исключением колес, цветовая гамма соответствует давлению (Pressure). На дороге, частицах и плоскости симметрии (на заднем плане данных рисунков) цветовая гамма соответствует модулю скорости (Velocity: Magnitude).
Результаты расчета движения автомобиля в колонне, показанные на рис. 1, а, б, соответствуют моменту времени 0,397 с от момента въезда её на мокрый участок дороги. Как видно из рисунка, из-под заднего колеса из конусоидального инжектора с заданной скоростью вылетают частицы, которые за счет заданных граничных условий прилипания оседают на дороге и поверхности транспортного средства. На данном этапе большинство частиц находится на малой высоте. Частицы, вылетевшие под наибольшим углом к горизонту, прилипают к нижней части кузова. По мере развития процесса угол разлёта частиц уменьшается, так как их движение в большей степени определяется внешним полем скоростей, а не инерцией.
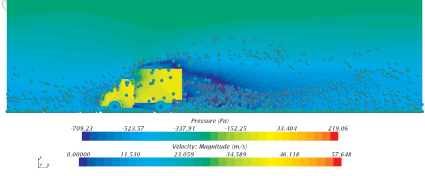
Рис. 2а. Динамика движения и оседания частиц воды на автомобиль (t = 5,5 с)

Рис. 2б. Динамика движения и оседания частиц воды на автомобиль (t = 5,5 с)
По мере развития процесса формируется поток частиц, который переходит через циклическую границу и достигает поверхности автомобиля, оседая на нём. Динамика данного процесса продемонстрирована на рис. 2, а, б. Результаты численного моделирования соответствуют времени 5,5 с. На данном рисунке наглядно видно, что частицы подхватываются вихревым потоком. По мере удаления от задней части автомобиля существенная доля частиц оседает на дороге. Тем не менее количество частиц, подхваченных вихревыми потоками и долетевших до следующего автомобиля в колонне, достаточно велико.
В рамках данной работы смоделировано движение частиц грязи с учётом аэродинамических эффектов обтекания автомобиля и взаимодействия частиц грязи с газовой фазой. На основе расчётов продемонстрировано, что в наибольшей степени загрязняется передний бампер, лобовое стекло, верхняя передняя часть кузова и тыловая часть бокового зеркала. Выявление зон, загрязняемых в меньшей степени, представляет существенную сложность в рамках используемой модели лагранжевой многофазности. Для их выявления потребовалось бы увеличить число частиц грязи в расчёте, что потребовало бы большего времени вычислений.
Исследования выполнены при финансовой поддержке Министерства образования и науки РФ в рамках проекта по договору № 02.G25.31.0006 от 12.02.2013 г. (постановление Правительства Российской Федерации от 9 апреля 2010 года № 218).
Рецензенты:
Петрухин Н.С., д.ф.-м.н., научный руководитель Нижегородского филиала Национального исследовательского университета «Высшая школа экономики», г. Нижний Новгород;
Карпухин В.Б., д.ф.-м.н., профессор кафедры «Высшая и прикладная математика» Российской открытой академии транспорта Московского государственного университета путей сообщения, г. Москва.
Работа поступила в редакцию 12.11.2014



