Начиная с первых работ (см. обзор [5]), посвященных разработке уравнений состояния скейлингового вида, удовлетворяющих масштабной теории критических явлений, их авторы пытались использовать в качестве опорной кривой термическую спинодаль, положение которой на термодинамической поверхности определяется равенством
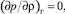(1)
где p – давление; ρ – плотность; T – абсолютная температура.
При этом в силу того, что в рамках МТ изохорная теплоемкость Cv имеет особенность в критической точке, то спинодаль отождествляли с линией сингулярности Cv, т.е. с геометрическим местом точек, в которых выполняется равенство
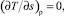(2)
где s – энтропия.
Линию, в каждой точке которой выполняются равенства (1) и (2), назвали псевдоспинодалью. Однако в работе [9] показано, что имеет место следующее утверждение: в каждой точке линии псевдокритических точек (линии сингулярности изохорной теплоемкости) выполняются равенства
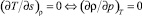, (3)
и только в критической точке одновременно выполняются равенства (1) и (2). Отметим, что в работах [10, 11, 12] метод псевдокритических точек [9] получил свое физическое обоснование.
И именно на основе соотношений (3) были сконструированы масштабные функции в физических переменных [2, 4, 7, 8], в том числе и не содержащие в своей структуре интегралов от дифференциальных биномов [2, 4], которые уступают по своим расчетным характеристикам наиболее удачным масштабным функциям, полученным в рамках параметрического представления масштабной гипотезы [15].
Таким образом, до настоящего времени не удалось построить масштабное уравнение, в котором роль опорной кривой выполняет спинодаль (1), а не линия псевдокритических точек (3). Решению этой задачи и посвящена данная работа.
Материал и методы исследования
Рассмотрим обобщенную модель масштабного уравнения (МУ), используя в качестве базовой функции изотермическую сжимаемость Kt:
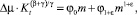(4)
где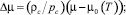 
ρc, pc – критические плотность и давление соответственно; μ – химический потенциал; μ0(T) – регулярная функция; β, γ – критические индексы; ε – варьируемый параметр.
Параметр m в формуле (4) согласно [6] задается равенством
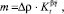(5)
где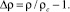 
Подставляя (5) в (4), получим
(6)
Решим (6) относительно Δμ:
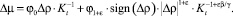(7)
Учтем, что согласно экспериментально подтвержденной гипотезе [13] об одинаковом характере поведения изотермической сжимаемости на критической и околокритических изохорах в асимптотической окрестности критической точки справедлива зависимость [11]:
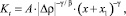(8)
где x – масштабная переменная; A и x1 – постоянные.
Подставим (8) в (7) и проведем ряд преобразований:
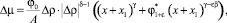(9)
где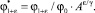 
Или, учитывая, что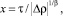 
получим из (9)
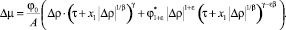(10)
Так как
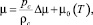(11)
а свободная энергия Гельмгольца F связана с химическим потенциалом выражением
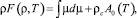(12)
где A0(T) – регулярная функция температуры, подставляя (11) в равенство (12), получим:
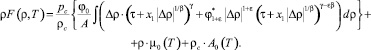(13)
Перейдем в (13) к новой переменной t:
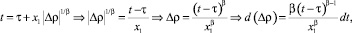(14)
и в результате получим
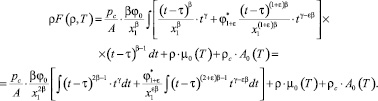(15)
Представляя интегралы от дифференциальных биномов, в виде ряда получим следующее выражение для свободной энергии Гельмгольца:
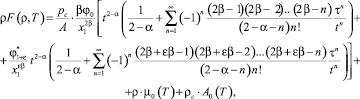(16)
где α – критический индекс изохорной теплоемкости.
Перейдем в (16) от переменной t к масштабной переменной x:
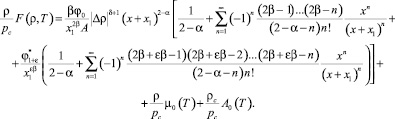(17)
Так как имеет место термодинамическое равенство
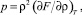(18)
то, подставляя (13) в (18), найдем выражение для давления:
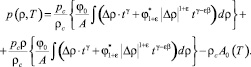(19)
Для того, чтобы найти выражение для изотермической сжимаемости Kt, необходимо найти частную производную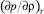 
:
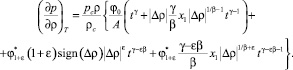(20)
Если имеет место неравенство
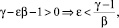(21)
то согласно (21) в каждой точке линии
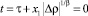(22)
выполняется равенство (1). Это означает, что в случае если параметр ε удовлетворяет условию (21), то уравнение (22) описывает на термодинамической поверхности термическую спинодаль (1), а не линию псевдокритических точек (3).
Неизвестный параметр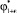 
можно найти из условия равенства нулю на линии насыщения x = –x0 масштабной функции h(x) химического потенциала, которая согласно (9) имеет вид
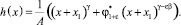(23)
Таким образом, учитывая равенство h(–x0) = 0 и выражение (23), имеем
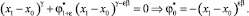(24)
Так как энтропия и свободная энергия Гельмгольца связаны термодинамическим равенством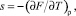 
выражение для энтропии s имеет вид
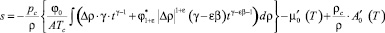. (25)
Подставляя (25) в термодинамическое равенство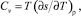 
получим следующее выражение для сингулярной составляющей изохорной теплоемкости
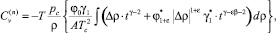(26)
где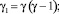 
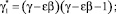
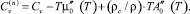
Воспользуемся соотношениями (14) и представим (26) в виде
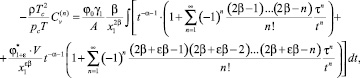(27)
где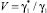 
.
Вычислим входящий в (27) интеграл и придем к следующему выражению:
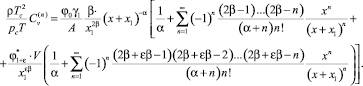(28)
В правую часть (28) входит сомножитель (x + x1)–α, который расходится при x → x1. Однако изохорная теплоемкость согласно (3) остается конечной на линии x = –x1, за исключением критической точки (Δρ = 0; τ = 0). В этом можно непосредственно убедиться, оценив интеграл, входящий в формулу для теплоемкости (26). При этом необходимо учесть, что α ≈ 0,1; γ ≈ 1,24.
Проверим адекватность предложенной модели масштабного уравнения состояния (10) при выполнении условия (21). Если критические индексы принимают значения α = 0,11 и γ = 1,326, то условие (21) выполняется при ε = 1; а при α = 0,11 и γ = 1,446 условие (21) выполняется при ε = 2. Однако если ε = 2, то из (7) непосредственно следует представление масштабной гипотезы в форме, предложенной в [15] и широко используемой при описании критических явлений [1, 3, 14].
Заключение
Доказана принципиальная возможность построения масштабного уравнения состояния в физических переменных плотность – температура, в котором в качестве опорной линии используется не линия сингулярности изохорной теплоемкости, а термическая спинодаль (1). Важным обстоятельством является то, что предложенное уравнение строго рассчитано в рамках феноменологической теории критических явлений, базирующейся на результатах работы [6].
Рецензенты:
Борзенко Е.И., д.т.н., профессор, зав. кафедрой криогенной техники ИХиБТ, НИУ ИТМО, г. Санкт-Петербург;
Цветков О.Б., д.т.н., профессор, зав. кафедрой теоретических основ тепло- и хладотехники ИХиБТ, НИУ ИТМО, г. Санкт-Петербург.
Работа поступила в редакцию 18.11.2014