Многообразие объектов с различными динамическими и статическими свойствами породило многообразие методов синтеза систем, нацеленных на определённые классы объектов. Одним из методов синтеза, ориентированных на описание объектов в пространстве состояний, является метод размещения полюсов основанный на применении полной обратной связи по состоянию и формулы Аккермана [2]. Этот метод позволяет определить матрицу коэффициентов обратных связей по описанию системы в пространстве состояний и желаемому расположению корней характеристического уравнения. Ограничением в применении обратных связей по состоянию является то, что эта обратная связь по своему действию обычно эквивалентна идеальным ПД и ПИД-регуляторам, которые имеют бесконечную полосу пропускания, тогда как реальные объекты и регуляторы всегда имеют конечную полосу пропускания. Кроме того, на практике обычно используется информация только о входных, выходных сигналах и ограниченном числе переменных. Поэтому задача синтеза реальных последовательных стабилизирующих алгоритмов на основе расчёта управляющих алгоритмов с использованием формулы Аккермана остается актуальной.
Рассмотрим задачу синтеза на примере системы управления объектом с одним входом и одним выходом, декомпозиция которого представима в виде последовательного соединения минимально-фазовых или интегрирующих звеньев первого порядка, с заданными динамическими показателями качества системы: временем регулирования – tp и перерегулированием – σ.
Определим структуру и параметры последовательного реального управляющего алгоритма системы путём расчёта вектора обратных связей по состоянию методом Аккермана и перехода от параллельного стабилизирующего алгоритма в форме линейной комбинации переменных состояния к последовательному алгоритму.
Методика синтеза последовательного управляющего алгоритма
Рассмотрим в обобщенном виде структурную схему замкнутой системы со стабилизированной матрицей коэффициентов обратных связей по состоянию. Данная замкнутая система эквивалентна алгоритмической структуре с главной отрицательной обратной связью исходной структуры и последовательными стабилизирующими алгоритмами инверсного вида:
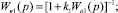
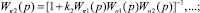
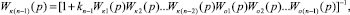
где Wo1(p), Wo2(p), ..., Won(p) – элементарные динамические первого порядка минимально-фазовые или интегрирующего вида передаточные функции объекта; Wк1(p), Wк2(p), ..., Wк(n–1)(p) – реальные составляющие последовательного управляющего алгоритма; [k1, k2, ..., kn] – вектор коэффициентов отрицательных обратных связей по состоянию исходной структуры [1, 3].
Покажем справедливость этого утверждения. Пусть исходная структурная схема системы имеет вид, приведенный на рис. 1.
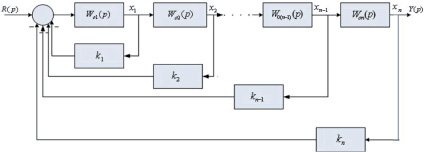
Рис. 1. Структурная схема исходной системы
Математическое описание первого контура системы приведено к виду
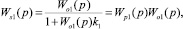
где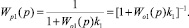 
Математическое описание 2-го преобразованного контура системы приведено к виду
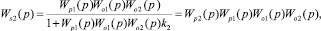
где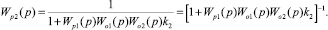 
Математическое описание (n–1)-го преобразованного контура системы имеет вид
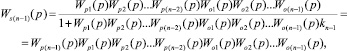
где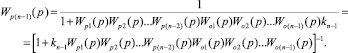 
С учетом полученных передаточных функций преобразованных контуров обратной связи эквивалентная структурная схема системы примет вид, изображенный на рис. 2.
Рис. 2. Эквивалентная преобразованная структурная схема системы
На основании преобразования структурной схемы стабилизированной замкнутой системы автоматического управления к эквивалентной структурной схеме с единичной отрицательной обратной связью и последовательно включенным звеном с передаточной функцией, обратной передаточной функции цепи обратной связи, предлагается следующая методика синтеза:
1. Провести декомпозицию передаточной функции объекта управления, формируя последовательно соединённые минимально-фазовые или интегрирующие звенья первого порядка.
2. Составить графы объекта и замкнутой системы с отрицательными обратными связями по состоянию.
3. По графу объекта определить систему дифференциальных уравнений в форме Коши.
4. Записать дифференциальное уравнение замкнутой системы в векторной форме.
5. Используя требуемые показатели качества, определить расположение полюсов замкнутой системы на комплексной плоскости.
6. Провести расчёт параметров обратных связей по формуле Аккермана.
7. Проверить результат синтеза по переходной характеристике системы.
8. На основе утверждения об эквивалентности структурных схем произвести расчёт передаточных функций последовательного стабилизирующего алгоритма.
9. Сопоставить результаты синтеза системы с последовательным стабилизирующим алгоритмом по переходной характеристике и исследования системы с безынерционными обратными связями по состоянию. Если разность переходных характеристик моделей системы с различными видами стабилизации окажется в пределах погрешностей программной системы, то проектные расчёты считаются достоверными.
Рассмотрим применение методики на примере системы приемочного контроля [2]. Структура нестабилизированной системы приёмочного контроля изображена на рис. 3. В результате синтеза необходимо найти такие значения коэффициентов обратной связи, при которых реакция системы на ступенчатый входной сигнал имела бы время регулирования по критерию 2 % менее 2,2 с и перерегулирование менее 4,5 %.
Рис. 3. Структурная схема разомкнутой системы автоматического контроля
Согласно предложенной методике получим модель объекта и системы в виде сигнального графа. Модель замкнутой системы в форме сигнального графа представлена на рис. 4. По сигнальному графу (структурной схеме) построим модель объекта в пространстве состояний. В качестве переменных состояния выбираем x1 = θ, x2 = dθ/dt, x3 = if(t). Все эти переменные доступны измерению, поэтому можно записать уравнение обратной связи в виде
u = [–k1 –k2 –k3]x = Kx.
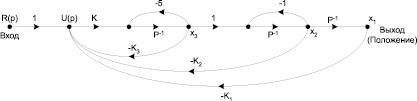
Рис. 4. Сигнальный граф замкнутой системы автоматического контроля
С учетом представленных обозначений модель замкнутой системы в пространстве состояний имеет вид
Реакция системы 3-го порядка может быть аппроксимирована с помощью доминирующих корней системы 2-го порядка, если действительная часть комплексных корней не превышает 1/10 действительного корня.
Определим область требуемого расположения доминирующих корней на p-плоскости (рис. 5). В заштрихованной области перерегулирование не превышает заданного значения.
На основании требований к качеству переходного процесса используя приближенные соотношения: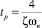 
и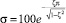 
находим значения ζ > 0,72 и ωп > 2,8.
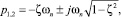
где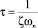 
– постоянная времени, соответствующая доминирующим корням характеристического уравнения
.
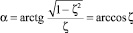Таким образом, численные значения двух доминирующих и одного недоминирующего полюсов характеристического уравнения составят: p1 = –2 + 2i, p2 = –2 – 2i, p3 = –20.
По формуле Аккермана (для k = 240) произведем расчёт параметров корректирующих обратных связей и определим переходную функцию замкнутой системы. Получены коэффициенты обратных связей: k1 = 0,6667, k2 = 0,2708, k3 = 0,0750. Моделирование работы системы в среде MatLab подтверждает соответствие показателей качества исследуемой системы заданным (σ = 4,27 %; tр = 2,16 с).
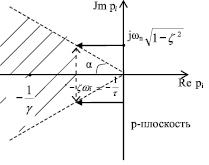
Рис. 5. Расположение доминирующих корней на p-плоскости
На основе утверждения об эквивалентности структурных схем проведём расчёт передаточных функций последовательного стабилизирующего алгоритма приведенным ранее формулам.
Для первого контура (kос = k3),
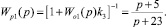
Для второго контура (kос = k2),
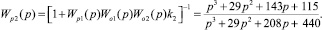
На рис. 6 приведены график переходного процесса системы с последовательным стабилизирующим алгоритмом (верхний), график переходного процесса системы с полной обратной связью по состоянию (средний) и кривая расхождений переходных характеристик.
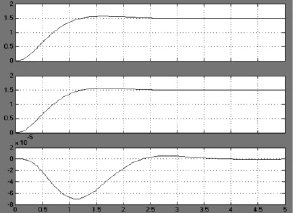
Рис. 6. Переходные характеристики системы с различными алгоритмами управления и график расхождений характеристик
Моделирование работы системы с последовательным стабилизирующим алгоритмом и с безынерционными обратными связями по переменным подтверждает идентичность реакций системы с допустимой погрешностью среды вычислений.
Рецензенты:
Казанцев В.П., д.т.н., доцент, профессор кафедры «Микропроцессорные средства автоматизации», ФГБОУ ВПО «Пермский национальный исследовательский политехнический университет», г. Пермь;
Бочкарёв С.В., д.т.н., доцент, профессор кафедры «Микропроцессорные средства автоматизации», ФГБОУ ВПО «Пермский национальный исследовательский политехнический университет», г. Пермь.
Работа поступила в редакцию 06.11.2014.