Вместе с активным развитием в мире всех отраслей промышленности широкое применение все больше и больше получают методы кибернетики в химии и химической промышленности. В результате была создана новая отрасль науки, названная кибернетикой химико-технологических производств. Именно эта наука стала базой для анализа и оптимизации химических производств с использованием математического моделирования.
Математическое моделирование как новый метод исследования является важнейшим достижением кибернетики. Суть моделирования сводится к замене реальной системы или, в нашем случае, технологического процесса (объекта) к некоторой искусственной системе и дальнейшему изучению модели на компьютере для получения новой информации об этой системе или технологическом процессе (объекте). При этом стоит заметить, что моделирование позволяет проводить эксперименты с моделью системы тогда, когда делать это на реальном объекте не представляется возможным.
В данной работе представлено моделирование участка учебно-экспериментальной установки в пакете Matlab Simulinc Simscape с использованием данных, полученных в результате гидравлического расчета системы трубопроводов.
Рассмотренная учебно-экспериментальная установка разработана и внедрена для исследования и оптимизации системы управления имитацией технологического процесса подготовки бумажной массы. Конструктивно установка состоит из пяти емкостей, соединенных между собой системой трубопроводов и набором технических средств автоматизации (датчики, исполнительные механизмы) [3].
Движение жидкости по трубопроводу экспериментальной установки осуществляется за счет перепада уровней энергии в начале трубопровода и в конце, который создается в результате работы насоса [6].
При гидравлическом расчете системы трубопроводов поставлена задача определения потерь напора в простом трубопроводе постоянного сечения на участке между емкостями экспериментальной установки. Для этого используется уравнение Бернулли [2], имеющее следующий вид:
Hпотр = Hст + K∙Qm, (1)
где K ‒ величина, называемая сопротивлением трубопровода; Q ‒ расход жидкости; m ‒ показатель степени, который имеет разные значения в зависимости от режима течения; Hст – статический напор, представленный как некоторая эквивалентная геометрическая высота.
Как уже отмечалось выше, перепад уровней энергии, за счет которого жидкость течет по трубопроводу, создается работой насоса (рис. 1). Основным уравнением для расчета всасывающих трубопроводов также является уравнение Бернулли. Основное правило при устойчивой работе насоса: при установившемся течении жидкости в трубопроводе насос развивает напор, равный потребному [8, 11].
Hнас = Hпотр. (2)
На этом равенстве основывается метод расчета трубопроводов с насосной подачей.
Для нашей системы выполнен гидравлический расчет технологического трубопровода на примере первых двух емкостей с насосом.
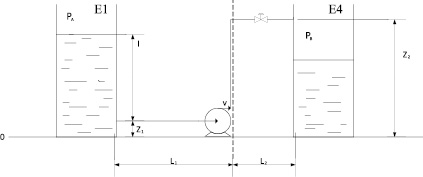
Рис. 1. Схема трубопровода между технологическими емкостями E1 и E4
Приведем для расчета начальные данные:
Давление в первой и второй емкостях E1 и E4 одинаково и равно PA = PB = 1,2∙105 Па; длина трубы от емкости E1 до насоса: L1 = 0,9 м, длина трубы от насоса до емкости E4: L2 = 0,1 м; диаметр труб d = 0,02 м; площадь сечения труб F = 3,14∙10–4 м2; расход перекачиваемой воды q = 2,81∙10–4 м3/с. Справочные значения плотности и динамической вязкости воды равны соответственно ρ = 998,2 кг/м3 и μ = 1∙10–3 Па∙с.
В технологической схеме присутствуют различные виды местных сопротивлений: вентиль нормальный; отвод φ = 90°, закругление трубы на небольшой градус. Высота подъема жидкости: ∆Z = 1,2 м.
Для нахождения скорости течения жидкости в трубе используется формула расхода:
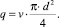(3)
Выразив из формулы 3 скорость, получено уравнение следующего вида [7]:
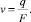(4)
Подставив в уравнение (4) начальные данные, получена следующая скорость:
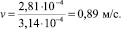
Напор, требуемый для преодоления сопротивления столба жидкости, определяется по формуле
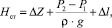
где Δl = l2 – l1 = –1 м.
Тогда Hст = 0,2 м.
Основной расчетной формулой для потерь напора при турбулентном течении жидкости в круглых трубах является эмпирическая формула, называемая формулой Вейсбаха – Дарси и имеющая следующий вид [9, 12]:
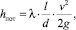(5)
где λ – коэффициент гидравлического трения; d – диаметр трубы; v – скорость движения жидкости; l – длина трубы.
Для расчета коэффициента гидравлического трения необходимо рассчитать число Рейнольдса по следующей формуле [5]:
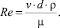(6)
Подставив в уравнения начальные данные, получаем число Рейнольдса: Re = 17767,96. Отсюда можно сделать вывод, что течение жидкости является турбулентным.
Кроме этого коэффициент гидравлического трения зависит от относительной шероховатости Δ/d (или Δ/r0, где r0 – радиус трубы). Поскольку в установке используются новые металлопластиковые трубы, то коэффициент шероховатости примем Δ = 7∙10–6 м, а коэффициент абсолютной шероховатости Δэ = 3,5∙10–6 м.
Тогда критический коэффициент Рейнольдса, рассчитанный по формуле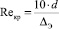 
, будет равен 57142.
В соответствии с таблицей определения коэффициента гидравлического трения, если число Рейнольдса лежит в диапазоне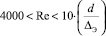 
, то коэффициент λ определяется по полуэмпирической формуле Блазиуса:
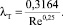(7)
Подставив известные данные в уравнение 7, получаем коэффициент гидравлического трения λТ = 0,027.
Тогда потери на участке трубопровода
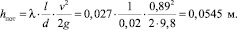
Для расчета потерь напора в местных сопротивлениях необходимо выбрать справочные значения коэффициентов местных потерь для соответствующих местных сопротивлений: ξ1 = 0,5 – коэффициент местных потерь для элемента – вход в трубу; ξ2 = 5 – коэффициент местных потерь для вентиля нормального; ξ4 = 1,2 – коэффициент местных потерь для поворота трубы на φ = 90°; ξ5 = 0,2 – коэффициент местных потерь для закругления трубопровода; ξ6 = 1 – коэффициент местных потерь для элемента – выход из трубы;
Тогда для всего трубопровода
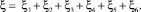(8)
Местные потери на всей протяженности трубопровода рассчитываются по следующей формуле:
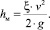(9)
Подставив в уравнение (9) данные, получим потери напора в местных сопротивлениях hм = 0,319 м.
Тогда общие потери напора в трубопроводе будут складываться из потерь напора на участке трубопровода и потерь напора на местных сопротивлениях:
h = hм + hпот + hст = 0,566 м.
В результате получаем, что потребный напор равен общим потерям напора в трубопроводе.
Для технологического процесса учебно-экспериментальной установки было проведено моделирование локальных контуров [4]. Все объекты были описаны с помощью математических формул, однако в модели не были учтены потери напора в трубопроводе и местные потери напора жидкости, поэтому было проведено моделирование гидравлической системы учебно-экспериментальной установки в пакете Matlab Simulink в среде моделирования Simscape с библиотекой Sim Hydraulics [10]. Данная среда предоставляет набор модулей для моделирования и симуляции физических систем, содержащих механические, гидравлические, электрические и другие компоненты. Simscape позволяет описать физическую структуру системы на более высоком уровне, чем математические выражения, лежащие в основе этой системы.
С помощью библиотеки Sim Hydraulics была собрана модель гидравлической системы учебно-экспериментальной установки. Схема модели экспериментальной установки в среде Simulink приведена на рис. 2. Результаты моделирования представлены на рис. 3.
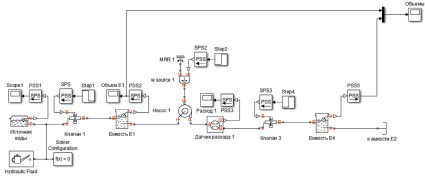
Рис. 2. Схема модели учебно-экспериментальной установки в среде Simulink
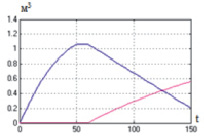
Рис. 3. График изменения объема жидкости в емкостях E1, E4
В результате проведенной работы были рассчитаны потери напора в трубопроводе учебно-экспериментальной установки. Полученные результаты позволили оценить влияние внешних и внутренних факторов на технологический процесс. На основе проведенных расчетов проводят выбор насоса, который будет обеспечивать требуемый напор в трубопроводе.
С учетом гидравлических расчетов было проведено моделирование участка технологического процесса, получены графики, на основании которых будет проводиться дальнейшее исследование системы, направленное на разработку систем автоматического регулирования технологического процесса, а именно на расчет ПИД-регуляторов.
Компьютерное моделирование технологических систем является актуальным и перспективным направлением, поскольку оно позволяет повысить точность и качество управления процессами. В свою очередь математические модели позволяют проводить исследования системы или технологического процесса быстро и без существенных затрат.
Рецензенты:
Бульбович Р.В., д.т.н., профессор, декан аэрокосмического факультета, ФГБОУ ВПО «Пермский национальный исследовательский политехнический университет», г. Пермь;
Цаплин А.И., д.т.н., профессор, зав. кафедрой общей физики, ФГБОУ ВПО «Пермский национальный исследовательский политехнический университет», г. Пермь.
Работа поступила в редакцию 06.11.2014.