Векторное управление является на сегодняшний день одним из самых востребованных методов управления двигателями переменного тока, применяемых в преобразователях частоты. Современная линейка преобразователей частоты ведущих фирм производителей, таких как Danfoss, ABB, Siemens, включает в себя адаптивные методики настройки регуляторов по параметрам схемы замещения двигателя переменного тока, что в совокупности с методами автоидентификации этих параметров и использованием метода векторного управления дает высокое качество управления.
Современные системы управления частотно-регулируемого привода (СУ ЧРП) с использованием векторного управления требуют применения высокопроизводительных микропроцессорных систем. Для реализации цифрового управления двигателем в составе управляющей аппаратной части необходимо иметь высокоточные и высокочастотные аналогово-цифровые преобразователи, генераторы ШИМ, микропроцессор с высокой производительностью. Вместе с этим становятся все более доступны по цене и характеристикам цифровые сигнальные процессоры (DSP), их производительность растет, что позволяет использовать их в системах управления двигателем и создавать на их основе СУ ЧРП.
В аппаратной части подобные системы имеют схожую архитектуру [8], и поэтому на передний план выходит алгоритмическое обеспечение данных систем управления. Программная реализация управления и желание повысить функциональные возможности и адаптировать СУ ЧРП к задачам управления двигателем заставляет обратить внимание на методы имитационного моделирования, позволяющие проводить практическое и виртуальное проектирование электромеханических систем управления [4, 6].
Одним из классов систем векторного управления является управление синхронным двигателем с постоянными магнитами или вентильным двигателем (ВД). Следует отметить что в алгоритмах векторного управления вентильным двигателем отсутствует блок оценки потокосцепления ротора, что существенно облегчает реализацию системы управления, при этом повышается качество самого управления.
В данной работе исследуется один из способов построения векторного управления вентильным двигателем (ВД) на основе настройки регуляторов скорости и тока по параметрам схемы замещения синхронного двигателя.
Для моделирования и отладки алгоритмов векторного управления ВД используем визуальную среду разработки и моделирования программного обеспечения для встраиваемых систем управления электроприводами MexBIOS Development Studio [3]. Для целей проектирования систем управления электроприводами среда MexBIOS Development Studio предоставляет пользователю множество удобных инструментов разработки: создание собственных программ управления электродвигателями, моделирование работы системы управления и электромеханических объектов и систем, выполнение отладки программы, загруженной в микроконтроллер, создание собственных библиотек компонентов.
Структурная схема системы векторного управления представлена на рис. 1.
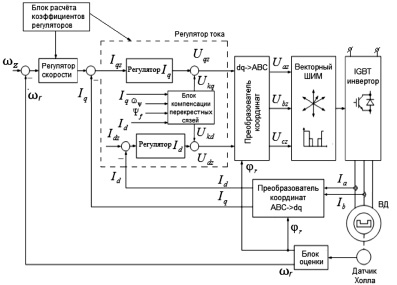
Рис. 1. Структура системы векторного управления
Для настройки регуляторов скорости и тока необходимо знать параметры двигателя: LSd – индуктивность статора по оси d; LSq – индуктивность статора по оси q; RS – сопротивление статора; ψf – потокосцепление. В современных СУ ЧРП данные параметры могут находиться на этапе идентификации двигателя. Широко известны методики идентификации [2], с помощью которых можно сделать достаточно точную оценку параметров машины переменного тока. Параметры двигателя могут быть получены в том числе и из паспортных данных. В системе векторного управления в данной работе параметры двигателя известны и не требуют уточнений.
Рассмотрим коротко процедуру синтеза регулятора скорости. Для этого запишем основное уравнение динамики движения электропривода в виде [1]:
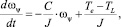(1)
где С – коэффициент трения; Te – электродинамический момент; TL –момент сопротивления; ωψ – электрическая скорость вращения ротора; J – момент инерции.
Электрическая скорость вращения ωψ определяется согласно выражению ωψ = p∙ωr, где ωr – скорость вращения ротора; p – число пар полюсов двигателя.
При настройке регулятора скорости принимаем в качестве желаемой передаточной функции апериодическое звено [1]. В результате синтеза получаем ПИ-регулятор скорости с передаточной функцией:
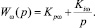(2)
Параметры регулятора определяем согласно выражениям
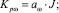
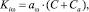(3)
где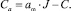 
Коэффициент αω выбирается как 1/50 от постоянной времени ПИ-регулятора тока. Реализация регулятора скорости в среде Mex BIOS Development Studio приведена на рис. 2.
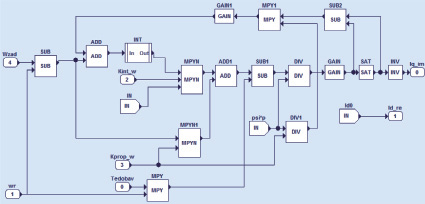
Рис. 2. Схема регулятора скорости в среде MexBIOS
Проведем синтез регуляторов тока в осях d и q. Запишем систему уравнений равновесия ЭДС статора в осях d–q:
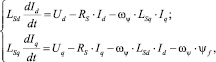(4)
где Ud – напряжение статора по оси d; Uq – напряжение статора по оси q; LSq – индуктивность статора по оси q; LSd – индуктивность статора по оси d; Iq – ток статора по оси q; Id – ток статора по оси d; RS – сопротивление статора; ωψ – электрическая скорость вращения, ψf – потокосцепление.
Для линеаризации системы уравнения и введения в систему регуляторов необходимо исключить из уравнений нелинейную часть:
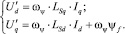(5)
Далее, так как продольные и поперечные индуктивности в неявнополюсной машине близки по значению, а в явнополюсной равны, то справедливо в первом приближении для расчета регулятора принять LSq = LSd.
При настройке регулятора тока принимаем в качестве желаемой передаточной функции апериодическое звено [1]:
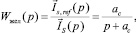(6)
где ac – частота среза апериодического звена.
При компенсации нелинейностей (5) в уравнениях (4) с учетом допущения равенства продольной и поперечной индуктивности уравнения примут в векторной форме вид
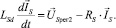(7)
На рис. 3 представлена общая структура регулятора тока совместно с моделью. Структура приведена в векторной форме, причем векторы тока и напряжения статора могут быть получены переходом от системы d–q координат на комплексную плоскость, где координата по оси d – действительная часть, а по оси q – мнимая часть комплексного числа, отображающего вектор.
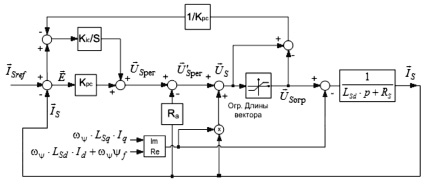
Рис. 3. Структура регулятора тока в векторной (комплексной) форме
Отношение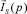 
к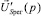 
выразится в виде передаточной функции
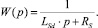(8)
С учетом добавочного сопротивления Ra, охватывающего отрицательной обратной связью передаточную функцию (8), отношение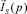 
к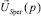 
примет вид
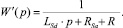(9)
Выполняя процедуру синтеза регулятора тока, для получения желаемой передаточной функции (6), вводим в структуру регулятора ПИ-звено.
Регулятор тока (рис. 3) снабжен блоком ограничения длины вектора, позволяющего ограничивать модуль вектора тока, сохраняя угол вектора неизменным. Такой подход дает возможность ограничивать ток статора, когда электрический угол ротора, поступающий на координатные преобразования отличается от реального угла. Для того чтобы убрать проблему избыточного увеличения интегральной составляющей регулятора, связанного с работой блока ограничения вектора напряжения, интегральная составляющая охватывается отрицательной обратной связью.
При настройке коэффициентов регулятора тока используем параметры двигателя
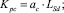
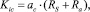(10)
где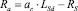 
– добавочное сопротивление, которое вводится в уравнение равновесия статора для приведения передаточной функции замкнутой системы к виду апериодического звена
Реализация регулятора тока в среде MexBIOS Development Studio приведена на рис. 4.
Создание проекта для микропроцессорного модуля (DSP) осуществляется сразу после этапа моделирования и отладки алгоритмов управления и предполагает загрузку управляющей программы в ОЗУ микропроцессора. Запуск проекта векторного управления ВД был осуществлен на базе отладочного комплекта MCB-02 с микропроцессором TMS320F28335 [7]. Данный комплект предназначен для разработки и тестирования программного обеспечения систем управления электродвигателем.
В начальный момент времени задание скорости составляет 40 рад/с, двигатель выходит на эту скорость без нагрузки. После выхода на заданную скорость, скачком выполняем наброс нагрузки (0,6 Н·м) в момент времени t = 0,4 с. По графикам (рис. 5) видно, что система отрабатывает сначала заданную на входе скорость, а затем и возмущающие воздействия в виде приращения нагрузки. Полученные результаты работы системы управления (рис. 5), реализованной на отладочном комплекте, подтвердили результаты моделирования.
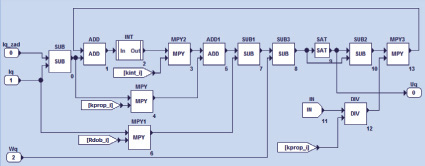
Рис. 4. Схема регулятора тока в среде MexBIOS
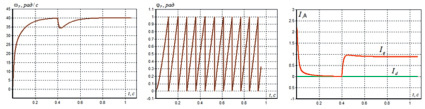
Рис. 5. Графики переходных процессов скорости, угла, токов
Заключение
В ходе исследования в среде визуального программирования MexBIOS Development Studio реализована структура векторного управления ВД, которая была сначала исследована с помощью средств моделирования данной среды и затем запущена на микропроцессорном модуле. Такой подход позволяет исключить ошибки и неточности при проектировании системы управления двигателем, а также произвести отладку программного кода во многих режимах работы системы управления. Наличие готовых шаблонов программного обеспечения, процедур из библиотек среды MexBIOS Development Studio значительно повышает скорость разработки СУ ЧРП.
Рассмотренная в работе система векторного управления ВД может быть использована для создания программной части СУ ЧРП в датчиковом режиме (с использованием энкодера или датчика Холла). Дальнейшее развитие данная система управления может получить добавлением алгоритмов идентификации параметров ВД и реализацией бездатчикового управления.
Рецензенты:
Бочкарев С.В., д.т.н., доцент, профессор кафедры микропроцессорных средств автоматизации, Пермский национальный исследовательский политехнический университет, г. Пермь;
Цаплин А.И., д.т.н., профессор, зав. кафедрой общей физики, Пермский национальный исследовательский политехнический университет, г. Пермь.
Работа поступила в редакцию 06.11.2014.