Для изделий из магнитомягкого материала (МММ) основная кривая намагничивания (ОКН) является одной из важнейших характеристик. Методика выполнения измерений при определении ОКН изделия из МММ предусматривает два основных этапа [4].
На первом этапе перед измерением ОКН необходимо выполнить размагничивание образца посредством перемагничивания его в знакопеременном поле, с амплитудой равномерно убывающей от максимального до минимального значения (рис. 1). Время размагничивания должно составлять не менее 40 с.
На втором этапе определение координат точек ОКН изделия из МММ начинают с наименьшего требуемого значения напряженности поля, постепенно переходя к большим значениям, при этом не допускается возврат от больших значений к меньшим [3].
Если в ходе первого этапа измерять амплитуду импульсов размагничивающего поля Hi и приращения индукции ΔBi, то можно, проанализировав эти данные, определить минимальное число точек ОКН, в которых требуется выполнить измерение для линейной аппроксимации ее с требуемой точностью.
Для этого были разработаны алгоритмы [4], позволяющие решить эту задачу. Работа алгоритма базируется на методе определения погрешности [5].
В основе первого алгоритма лежит анализ модуля второй производной изменения магнитной индукции B по напряженности H. Построив график зависимости d2B/dH2 от Н, вычисляем значение общей площади Sобщ по формуле
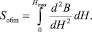
Задавшись количеством точек n, определяем значение площади Sизм, соответствующей одной измеряемой точке на ОКН:
Sизм = Sобщ/n.
Для нахождения координат точек, подлежащих измерению, воспользуемся формулой вычисления площади методом трапеции и уравнением прямой и составим систему уравнений:
 (1)
(1)
где 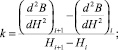
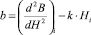 – коэффициенты, i = 1...N, N – количество точек, полученных в процессе проведения размагничивания.
– коэффициенты, i = 1...N, N – количество точек, полученных в процессе проведения размагничивания.
Решая систему уравнений (1), получим
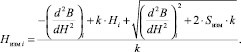
После определения первой и второй производных (рис. 1) и применения вышеописанного алгоритма получили результаты, представленные на рис. 2.
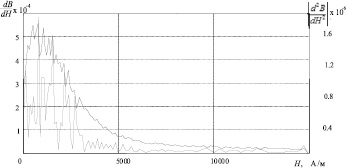
Рис. 1. Первая и вторая производные по H
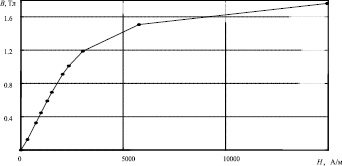
Рис. 2. Результат применения алгоритма при n = 10
Видно, что алгоритм работает некорректно. Данная «некорректность» вызвана сильным зашумлением результатов измерений ОКН. Для исправления положения произведем фильтрацию. На рис. 3 представлены функции первой и второй производных измеренной ОКН после проведения фильтрации, а на рис. 4 – результаты, полученные после использования фильтрованных функций первой и второй производных в адаптивном алгоритме.
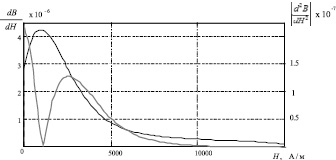
Рис. 3. Производные после фильтрации
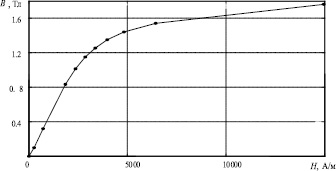
Рис. 4. Результат работы алгоритма при n = 10
Из рис. 4 видно, что алгоритм работает корректно, выделяя линейные и нелинейные участки ОКН и строя программу измерения таким образом, что на нелинейных участках проводится максимальное количество измерений.
Работа второго алгоритма базируется на методе определения погрешности и поясняется на рис. 5.
На этом рисунке использованы следующие обозначения: pk, pk = m – 2 – начальная и конечная точки аппроксимирующего отрезка (k Î [0, m – 2], i Î [k – 2, m]); m – количество шагов при размагничивании изделия из ФММ; pi–1 – точка ОКН, подлежащая проверке на принадлежность аппроксимирующему отрезку lki.
Работает алгоритм следующим образом.
1. Задаем начальные условия: k = 0, i = k + 2.
2. Строим аппроксимирующий отрезок lki.
3. Последовательно проверяем на принадлежность точек pi отрезку lki, до тех пор пока i < k.
4. Если все точки участка ОКН принадлежат lki, то принимается, что данный участок можно им заменить, принимаем k = k + 1, i = i + 1 и возобновляем процесс, начиная с пункта 2. Если хотя бы одна из точек данного участка ОКН не принадлежит lki, строится новый аппроксимирующий отрезок lki–1 и вновь выполняется проверка на принадлежность точек участка ОКН, ограниченного точками pk и p i–1. Проверка на принадлежность точки pi–1 отрезку lki с заранее заданной погрешностью аппроксимации δа выполняется, исходя из следующих соображений. Рассмотрим прямоугольные треугольники АСD и BCD. Геометрической интерпретацией погрешности аппроксимации является перпендикуляр hi-1 к lki из точки pi-1. Длина отрезка hi-1 вычисляется по формуле
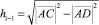
или
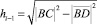 ,
,
следовательно,
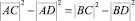 .
.
В свою очередь 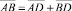 . Исходя из этого составим систему уравнений
. Исходя из этого составим систему уравнений
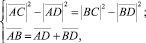
откуда
 ,
,
где 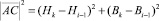 ;
;
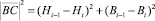 ;
;
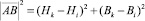 .
.
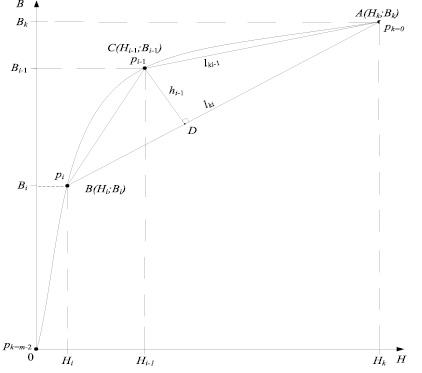
Рис. 5. Принцип работы алгоритма
После расчета hi-1 проверяется условие hi-1 < δа. При выполнении этого условия считаем, что точка pi-1 принадлежит аппроксимирующему отрезку с погрешностью δа.
Таким образом, предложенные алгоритмы сокращают количество измеряемых точек ОКН, увеличивая производительность операций контроля при погрешности измерения, не превышающей значения регламентируемого в [2].
Статья подготовлена с использованием оборудования ЦКП «Диагностика и энергоэффективное электрооборудование» ЮРГПУ(НПИ).
Рецензенты:
Горбатенко Н.И., д.т.н., профессор кафедры «Информационные и измерительные системы и технологии», ФГБОУ ВПО «Южно-Российский государственный политехнический университет (НПИ) им. М.И. Платова, г. Новочеркасск;
Гречихин В.В., д.т.н., профессор кафедры «Информационные и измерительные системы и технологии», ФГБОУ ВПО «Южно-Российский государственный политехнический университет (НПИ) им. М.И. Платова, г. Новочеркасск.
Работа поступила в редакцию 23.10.2014.



