Биметаллический элемент представляет две жестко соединенные металлические пластинки с различными коэффициентами температурного расширения. При нагреве биметаллическая пластинка изгибается за счет различного удлинения её составляющих. Благодаря этому свойству термобиметаллические элемен-ты широко используются как источники движения и механических усилий в конструкциях современных электротехнических устройств и приборов в качестве защитных реле и регуляторов температуры. Известно применение термобиметаллов в качестве чувствительных элементов теплоэнергетических приборов, для замера расхода, давления, плотности газов и жидкостей.
В настоящей работе представлены результаты исследования процесса упругого деформирования и напряжённого состояния биметаллической пластинки, диска и кольца. В качестве инструментов исследования используются известные аналитические модели, конечно-элементный метод перемещений (МКЭ) и современные программные комплексы Autodesk Mechanical Desktop 2006 и Cosmos Work 2006. Расчётные модели пластинки, диска и кольца представлены в виде ансамблей пространственных конечных элементов. Выполнен расчёт упругих перемещений и напряжений. Построены формы деформирования и эпюры напряжений. Результаты расчётов МКЭ сопоставлены с данными известных аналитических решений [1, 2].
В качестве примера взята пластинка, изготовленная из термобиметалла марки ТБ 1323 [1] с компонентами 19НХ/36Н, которые имеют следующие характеристики: модули упругости Е1/Е2 = 195/150 ГПа, температурные коэффициенты линейного расширения α1/α2 = (17/1,3) 10-6 К-1, толщины слоёв h1/h2 = 0,2/0,228 мм. В числителе указаны характеристики хромоникелевой стали 19НХ, в знаменателе – инвара 36Н. Вычислим перемещения λ и напряжения σmax при изменении температуры на ΔT = 180 К.
Для расчёта перемещений воспользуемся формулами:
![]() ,
,
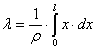 ,
,
где l=20 мм – длина пластинки, ρ – радиус кривизны упругой линии.
Максимальные напряжений возникают вблизи слоя спая и определяются формулой
![]()
Результаты вычислений представлены в таблице. В числителе приведены значения λ и σmax, полученные на основе аналитического решения, в знаменателе – на основе МКЭ. Констатируем, результаты вычислений хорошо согласуются друг с другом (различие по перемещениям составляет около 1%, по напряжениям – около 3%).
| Элемент | ΔТ, С0 | Перемещение λ (мм) | Напряжение σmax (МПа) |
| Пластинка | 180 | 1,981 / 2,001 | 257,5 / 249,2 |
СПИСОК ЛИТЕРАТУРЫ:
- Андреева Л.Е. Упругие элементы приборов. М.: Маши-ностроение, 1981 – 392 с.
- Феодосьев В.И. Избранные задачи и вопросы по сопро-тивлению материалов. М.: Наука. Физматлит, 1996 – 368 с.



