Для рек с малыми глубинами предложена сплоточная единица (СЕ), состоящая из четырех пучков малого объема (до 5 м3), соединенных между собой с помощью крепежных бревен и гибких связей [4].
В лаборатории кафедры водного транспорта леса и гидравлики выполнены экспериментальные исследования неустановившегося движения лесотранспортных единиц (ЛТЕ), которые формировались из 1…6 СЕ [2].
Исследования проводили на моделях в масштабе 1:20 при соотношениях глубины наполнения бассейна к осадке ЛТЕ h/Т = 7,0; 5,0; 4,0; 2,7; 1,6 и длины ЛТЕ к ее ширине L/В = 1…6. Моделирование при этом масштабе надежно с точки зрения масштабного эффекта, что доказано экспериментально на моделях и в натурных условиях [3].
При равномерном движении моделирование выполнено по критерию Фруда в интервале от 0,16 до 0,48, а при неустановившемся – по критериям Фруда и гомохронности. Опыты проведены при числах Рейнольдса 3,1•104…5,5•105.
Модели буксировались при поперечном расположении лесоматериалов в диапазоне скоростей 0,1…0,3 м/с.
Движение моделей фиксировалось бесконтактным оптическим датчиком оборотов. Датчик обеспечивал формирование импульсов, частота повторений которых пропорциональна частоте прохождения тахометрических меток, нанесенных на вращающийся блок со светоотражающим покрытием. Изменение частоты импульсов по времени фиксировалось на компьютере с помощью программы Zet Panel.
Надежное транспортирование ЛТЕ возможно при условии их управляемости. Это особенно важно в речных условиях при расхождении со встречными караванами на поворотах и участках со свальным течением. Управляемость ЛТЕ обеспечивается при достижении скорости буксировки в натурных условиях относительно потока 0,4…0,9 м/с. При выполнении технологических расчетов переместительных операций с ЛТЕ необходимо знать время и путь разгона ЛТЕ до скорости, при которой обеспечивается их управляемость.
Дифференциальное уравнение разгона ЛТЕ из состояния покоя [5]:
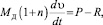(1)
где MД – масса ЛТЕ, кг; n – коэффициент нестационарности, учитывающий влияние массы воды МВ, заполняющей пустоты внутри ЛТЕ, присоединенной массы λ и дополнительного сопротивления ΔRнест, возникающего при неустановившемся движении ЛТЕ;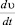 
– ускорение движения ЛТЕ, м/с2; Р – усилие буксировки ЛТЕ, Н; R – сопротивление воды равномерному движению ЛТЕ, Н;
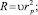(2)
r – приведенное сопротивление воды движению ЛТЕ, Н•с2/м2;
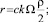(3)
с – коэффициент сопротивления; k – коэффициент, учитывающий влияние «мелководья»; Ω – характерная площадь (площадь сечения по миделю B?T), м2; ρ – плотность жидкости, кг/м3; νр – скорость равномерного движения, м/с.
Для каждой модели получены квадратичные зависимости силы сопротивления воды равномерному движению лесотранспортных единиц от скорости движения модели.
Сопротивление неустановившемуся поступательному движению лесотранспортных единиц представлено как сопротивление воды равномерному движению лесотранспортных единиц и дополнительное сопротивление, возникающее при неустановившемся движении.
Получена зависимость c = f(L/B) для «глубокой воды» при h/T = 7 (рис. 1) (коэффициент корреляции 0,973):
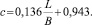(4)
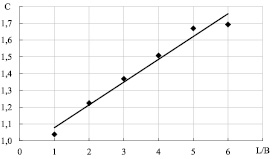
Рис. 1. Зависимость c = f(L/B)
По результатам обработки опытов получена зависимость k = f(h/T) (рис. 2) (корреляционное отношение 0,932).
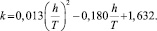(5)
При обработке результатов опытов по разгону моделей получили зависимости скорости и ускорения модели от времени вида:
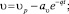
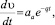
где аν, аа, q – параметры, определяемые экспериментально.
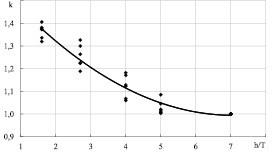
Рис. 2. Зависимость k = f(h/T)
По результатам исследований разгона ЛТЕ при соотношениях L/B = 1…6 и h/T = 1,6…7,0 получены значения коэффициента n [1].
Полученные зависимости аппроксимированы уравнениями вида
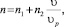(6)
где n1, n2 – параметры эмпирической формулы;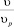 
– относительная скорость.
На рис. 3 приведены значения зависимости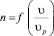 
, при достижении скорости равномерного движения ЛТЕ в натурных условиях νр = 0,45…1,2 м/с и соотношениях L/В = 3 и h/T = 7 (коэффициент корреляции 0,842). Зависимости вида (6) получены проф. Митрофановым А.А. для пучковых сортиментных плотов [3].
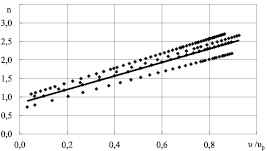
Рис. 3. Зависимость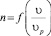 
при соотношениях L/В = 3 и h/T = 7
На рис. 4, 5 приведены зависимости n1 = f(L/B) и n2 = f(L/B) при h/T = 1,6…7,0. В результате получены расчетные формулы для определения параметров n1 и n2 (корреляционное отношение 0,856 и 0,811 соответственно):
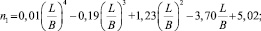(7)
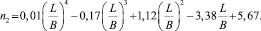(8)
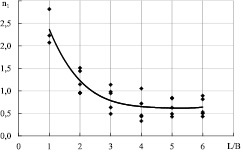
Рис. 4. Зависимость n1 = f(L/B)
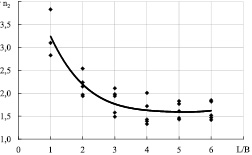
Рис. 5. Зависимость n2 = f(L/B)
В результате исследований получены зависимости для определения параметров n, c и k, позволяющие определить сопротивление воды равномерному движению, а также время и путь разгона ЛТЕ из состояния покоя до скорости, при которой обеспечивается их управляемость, при различных условиях эксплуатации. Можно решать и другие задачи, например найти необходимую силу разгона для достижения той или иной скорости движения ЛТЕ, близкой к равномерной за определенное время.
Рецензенты:
Копейкин А.М., д.т.н., профессор кафедры лесопильно-строгальных производств, ФГАОУ ВПО «Северный (Арктический) федеральный университет имени М.В. Ломоносова», г. Архангельск;
Мясищев Д.Г., д.т.н., профессор кафедры транспортных машин, ФГАОУ ВПО «Северный (Арктический) федеральный университет имени М.В. Ломоносова», г. Архангельск.
Работа поступила в редакцию 01.10.2014.