В системах обработки сигналов эффективность работы во многом зависит от сигналов поступающих на входы. Чем меньше размерность сигнала и чем больше его информативность, тем эффективнее работает система. Для этого используется предварительная обработка сигналов. Ее можно проводить с помощью различных преобразований. Одним из таких преобразований является вейвлет-преобразование. Вейвлет-анализ представляет собой особый тип линейного преобразования сигналов и отображаемых этими сигналами физических данных о процессах и физических свойствах природных сред и объектов.
Практическое использование вейвлет-преобразований в основном связано[1] с дискретными вейвлетами в силу повсеместного использования цифровых методов обработки данных. Для реализации алгоритма предварительной обработки сигналов, эффективно использовать ортогональные[2] вейвлеты. Для вейвлетов обладающих свойством ортогональности существует так называемое быстрое вейвлет-преобразование (Fast Wavelet Transform). Оно реализует основанный на фильтрации итерационный алгоритм, причем число итераций может быть произвольным.
Сигнал подается на фильтры декомпозиции низких и высоких частот, после чего с помощью операции децимации ![]() (уменьшения числа частотных составляющих вдвое) можно получить коэффициенты аппроксимации на выходе фильтра низких частот и детализирующие коэффициенты на выходе фильтра высоких частот [2]. Операция децимации выглядит следующим образом:
(уменьшения числа частотных составляющих вдвое) можно получить коэффициенты аппроксимации на выходе фильтра низких частот и детализирующие коэффициенты на выходе фильтра высоких частот [2]. Операция децимации выглядит следующим образом:
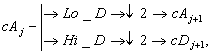
![]() - коэффициенты аппроксимации уровня j+1,
- коэффициенты аппроксимации уровня j+1, ![]() - детализирующие коэффициенты уровня j+1. В результате мы получим полный набор аппроксимирующих и детализирующих коэффициентов, вплоть до уровня декомпозиции j+1. По этому набору коэффициентов мы можем построить вейвлет-спектрограмму сигнала, например для оценки его особенностей.
- детализирующие коэффициенты уровня j+1. В результате мы получим полный набор аппроксимирующих и детализирующих коэффициентов, вплоть до уровня декомпозиции j+1. По этому набору коэффициентов мы можем построить вейвлет-спектрограмму сигнала, например для оценки его особенностей.
СПИСОК ЛИТЕРАТУРЫ:
- Дремин И.Л. Вейвлеты и их использование. / Успехи физических наук, 2001, т.171, №5.
- Mallat S A Wavelet Tour of Signal Processing (San Diego: Academic Press, 1998).



