Успешная подготовка в вузе бакалавров, специалистов и магистров во многом определяется эффективной организацией учебного процесса по дисциплинам основной образовательной программы. Обобщение результатов профессиональной деятельности позволяет преподавателю ориентировочно проектировать свое взаимодействие со студентами для достижения требуемого результата обучения. Включение математического моделирования в инструментарий педагогических исследований предоставляет возможность рассчитывать количественные показатели учебного процесса, что значительно повышает эффективность его планирования. Применение математических моделей для отображения существенных взаимосвязей дидактических процессов и систем стало возможным в связи с развитием методологии общей теории систем. Установление аналогий между исследуемыми и уже изученными объектами из других областей знаний создает условия для изучения общесистемных закономерностей, которые присущи сложным структурным образованиям различной природы [8].
Результаты и обсуждение
Моделирование дидактических систем, изменяющихся во времени, может осуществляться с помощью дифференциальных уравнений. В работе [9] для моделирования качества образования в вузе представлен пример использования логистического уравнения. Авторы выявили тенденции дальнейшего совершенствования образовательной деятельности на основе анализа результатов исследования данной математической модели. Полнота овладения содержанием дидактических единиц (ДЕ) или учебных тем в заданный временной интервал выступает показателем полноты освоения дисциплины [4] и является одной из составляющих качества образования, поэтому представляется целесообразным для исследования динамики формирования понятийной системы также применить логистическое уравнение.
Дифференциальное уравнение (ДУ), получившее название логистического, было предложено в 1848 году бельгийским математиком П.Ф. Ферхюльстом (1804–1849) [7]. Оно впервые учитывало системный фактор при моделировании ограничения роста численности популяции. В представленной модели популяция рассматривалась как открытая развивающаяся система. Изменение ее численности устремлялось к определенному пределу, который был призван характеризовать емкость ресурсов обитаемой экологической ниши. В данном исследовании аналогом ограничения роста численности популяции может выступать освоение фиксированного количества учебных элементов (УЭ) [2] в рамках какой-либо ДЕ. Совокупность УЭ – это система теоретических знаний и практических умений, формируемая в процессе обучения. Математическая модель в этом случае имеет вид
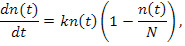(1)
где dn(t)/dt – скорость освоения УЭ; k – коэффициент пропорциональности, отображающий полноту овладения содержанием ДЕ; n(t) – количество УЭ, которые освоены студентами в момент времени t; (1 – n(t)/N) – относительная величина завершенности освоения УЭ в момент времени t; N – количество УЭ, которые необходимо освоить в рамках ДЕ.
Уравнение (1) представляет собой ДУ с разделяющимися переменными [3] и его частное решение с учетом начального условия n(0) = n0 имеет следующее выражение
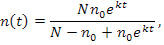(2)
где n0 – количество УЭ, которые необходимо освоить на предшествующем этапе обучения, для понимания содержания ДЕ.
Полноту освоения q(t) ДЕ в момент времени t можно рассматривать как относительную величину, определяемую по формуле
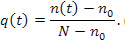(3)
Качеством освоения ДЕ за фиксированный промежуток времени [t0; tn], характеризующим полноту изучения содержания ДЕ за отмеченный период, в этом случае будет выступать величина Q, принимающая значение Q = q(tn). Проведение вычислений становится возможным при задании значений параметров математической модели k, n0, N. Коэффициенту k можно присвоить, например, значение единицы, если студент своевременно выполняет в полном объеме все предусмотренные тематическим планом контрольно-обучающие мероприятия, входящие в состав ДЕ. Если объем правильного выполнения запланированных заданий составляет только некоторую часть от целого, то коэффициенту k следует придать значение, равное этой части. Традиционное выделение трех градаций успешности обучения (первая – отлично, вторая – хорошо и третья – удовлетворительно) позволяет рассматривать следующие значения k: k1 = 1; k2 = 0,8; k3 = 0,6. Значение 0,8 соответствует доли оценки «4» относительно пяти, а значение 0,6 – доли оценки «3» относительно пяти. Значения параметров n0 и N устанавливаются на основе обобщения результатов анализа содержания ДЕ.
Например, ДЕ «Теория вероятностей» (ТВ), изучаемая студентами технических специальностей и направлений подготовки в рамках дисциплины «Математика», может включать двенадцать УЭ [1]. Содержание УЭ: 1) вероятность элементарного события; 2) действия над событиями; 3) вероятность суммы несовместных и совместных событий; 4) вероятность произведения независимых и зависимых событий; 5) правила комбинаторики, сочетания, размещения и перестановки; 6) независимые повторные испытания; 7) формула полной вероятности и формула Байеса; 8) теорема Пуассона, локальная и интегральная теорема Муавра-Лапласа; 9) закон распределения дискретной случайной величины и ее характеристики; 10) биномиальный закон распределения и закон Пуассона; 11) плотность распределения вероятностей непрерывной случайной величины и ее характеристики; 12) нормальный, равномерный и показательный законы распределения непрерывной случайной величины.
Успешность изучения студентами темы ТВ опирается на систему ранее освоенных УЭ на предшествующих этапах обучения: 1) графики основных элементарных функций; 2) нахождение производной функции; 3) вычисление определенного интеграла; 4) нахождение несобственного интеграла. Представленная совокупность УЭ определяет значение параметра n0 (n0 = 4) в уравнениях (2) и (3). Учитывая долю правильного выполнения учебных заданий на предшествующих этапах обучения, для трех градаций успешности обучения n0 будет равно соответственно n01 = 4; n02 = 3,2; n03 = 2,4. Значение параметра N в уравнениях (2) и (3) в этом случае можно принять равным 16 (N = 12 + 4 = 16).
Математические модели динамики полноты освоения ДЕ по теории вероятностей для трех градаций успешности обучения примут следующий вид
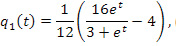
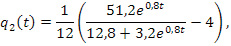
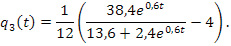
Графические модели функциональных зависимостей (4) – (6) представлены на рис. 1.
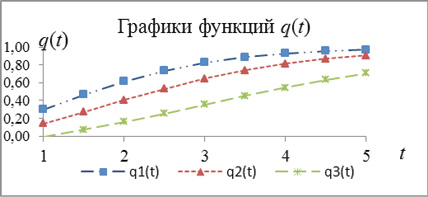
Рис. 1. Динамика полноты освоения ДЕ
Анализ функциональных зависимостей (4) – (6) показывает, что если t → ∞, то q(∞) = 1. Эта тенденция выполняется для всех трех функций и иллюстрирует тот факт, что познавательный процесс может продолжаться за временными рамками изучения ДЕ. Представленные графические модели (рис. 1) создают возможность наглядно увидеть расхождения кривых, характеризующих различную степень успешности освоения УЭ. Приближение к единице значения функции q1(5) позволяет ограничить интервал времени, отведенный на изучение ТВ, пяти условными единицами (у.е.).
Освоение студентами ДЕ может распределяться по двум, трем или четырем этапам учебной деятельности (УД) [4]. Первый этап УД – формирование системы знаний о вероятностных закономерностях. Второй этап УД – формирование умений применять вероятностные закономерности для решения стандартных математических задач и выполнения лабораторно-практических заданий. Третий этап УД – развитие интеллектуальных умений применять вероятностные закономерности при выполнении учебно-исследовательских заданий. Четвертый этап УД – развитие культуры мышления и творческих способностей при решении нестандартных математических задач [5] на установление вероятностных закономерностей. Переход на следующий этап УД может осуществляться достижением определенного значения такой величины как относительный объем q(t) освоения ДЕ. Представляется целесообразным рассматривать завершение первого этапа, если q(t) принимает значение более 0,4. Показателем окончания второго этапа может служить значение q(t) более 0,7. Если значение q(t) становится более 0,9, то это сигнализирует о том, что студент готов к движению на четвертом этапе.
Продолжительность отмеченных этапов УД определяется по функциональным зависимостям (4) – (6) с учетом уровня математической подготовки студентов. Например, если на изучение ТВ отводится 72 часа, то возможный вариант прохождения этапов УД для трех выделенных градаций обучающихся представлен в таблице.
Продолжительность этапов УД
|
Группа студентов |
Всего |
Этап УД |
||||||||
|
I |
II |
III |
IV |
|||||||
|
у.е. |
ч. |
у.е. |
ч. |
у.е. |
ч. |
у.е. |
ч. |
у.е. |
ч. |
|
|
k1 = 1 |
5 |
72 |
1,5 |
22 |
1 |
14 |
1,5 |
22 |
1 |
14 |
|
k2 = 0,8 |
5 |
72 |
2 |
30 |
1 |
14 |
2 |
28 |
– |
– |
|
k3 = 0,6 |
5 |
72 |
3 |
44 |
2 |
28 |
– |
– |
– |
– |
Динамика освоения ДЭ при изучении ТВ в каждом из пяти выделенных временных интервалов (рис. 1) для трех выделенных градаций успешности обучения производится по формуле
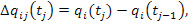(7)
где Δqij(tj) – динамика полноты освоения ДЕ у студентов, проявляющих i-ю градацию успешности в обучении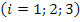 
в j-й единичный интервал времени Δtj 
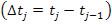; tj – j-й момент времени t. В нашем случае j принимает значения от 1 до 5 (пять единичных временных интервалов обеспечивают приближение q1(t) к единице), t0 – начальный момент времени. Графики функций Δq1j(tj), Δq2j(tj) и Δq3j(tj) представлены на рис. 2.
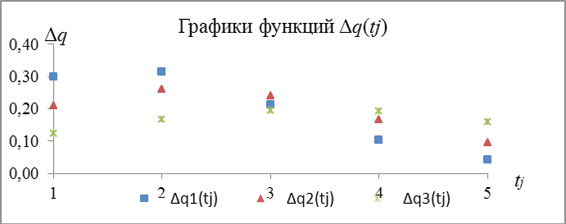
Рис. 2. Динамика полноты освоения ДЕ в единичные интервалы времени
Составленная математическая модель (7) адекватно отражает наблюдаемый в педагогической практике процесс овладения содержанием ДЕ студентами, имеющими различные учебные достижения.
Студенты, стремящиеся учиться на «отлично», достаточно быстро включаются в изучение новой темы. Хорошо сформированный понятийный аппарат и навыки логического мышления на предшествующих этапах обучения позволяют им находить различные взаимосвязи между уже известными и вновь вводимыми терминами. Это приводит к успешному освоению ДЕ и систематизации теоретических знаний и умений. Они самостоятельно и очень продуктивно решают учебные задачи различной сложности.
Студенты, которые учатся на оценку «хорошо», постепенно входят в изучение нового материала. Они имеют сформированную систему определений ранее изученных понятий, но им требуется время на повторение отдельных фрагментов учебных тем для понимания взаимосвязей УЭ, входящих в состав ДЕ. Они самостоятельно обращаются к справочному и учебно-методическому сопровождению образовательного процесса и находят ответы на интересующие их вопросы.
Студенты, чьи учебные достижения оцениваются удовлетворительно, на начальном этапе изучения нового учебного материала испытывают значительные трудности, так как имею пробелы в своей теоретической системе знаний и умений. Установление взаимосвязей ранее изученных понятий с новыми терминами происходит медленно. Студенты нуждаются в педагогическом сопровождении организации их учебной деятельности.
Заключение
Применение логистического уравнения при моделировании этапов освоения ДЕ позволяет преподавателю более рационально проектировать учебную деятельность студентов с учетом их успешности в обучении. Это создает условия для дальнейшего совершенствования программно-методического сопровождения учебного процесса. Эффективность включения математического моделирования в исследования дидактических закономерностей неразрывно связана с обобщением результатов педагогических наблюдений и использованием методов математической статистики для обработки эмпирических данных, полученных в ходе проведения педагогической диагностики [6] учебных достижений обучающихся.
Рецензенты:
Баутин С.П., д.ф.-м.н., профессор, профессор кафедры «Высшая и прикладная математика» Уральского государственного университета путей сообщения, г. Екатеринбург;
Титов С.С., д.ф.-м.н., профессор, заведующий кафедрой «Прикладная математика и техническая графика» Уральской государственной архитектурно-художественной академии, г. Екатеринбург.
Работа поступила в редакцию 29.07.2014.