Теория катастроф как раздел математики начала формироваться еще в середине ХХ века на основе теории особенностей гладких отображений и теории динамических систем. Основоположниками современной теории катастроф являются французский математик Р. Том [9] и российский математик В.И. Арнольд [1]. Катастрофами называются скачкообразные изменения, возникающие в виде внезапного ответа системы на плавное изменение внешних условий.
Одной из семи элементарных катастроф по Р. Тому [9] является катастрофа сборки, потенциальная функция которой определяется следующим образом:
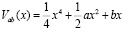, (1)
где x – переменная состояния;
a, b – переменные управления.
Многообразие M катастрофы задается уравнением:
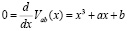, (2)
которое имеет от одного до трех вещественных корней. Природа этих корней зависит от дискриминанта:
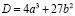. (3)
Катастрофа происходит, когда дискриминант D меняет знак с отрицательного на положительный [9].
Полагаем, что изменения управляющих переменных являются случайными. В качестве случайных величин [2] или случайных функций [3], [7] можно представить нагрузку, геометрические характеристики, параметры прочности, механические свойства материалов и т.д. Очевидно, что вследствие разброса возможных значений, конструкции будут работать с более или менее редкими перегрузками [5],[6]. Поэтому определенный интерес представляет изучение вопросов проектирования элементов конструкций технологических машин с позиций теории катастроф с учетом стохастической природы возмущающих факторов.
Оценка вероятности возникновения катастрофы сборки
Рассмотрим катастрофу сборки со стохастических позиций. Переменные управления a и b в общем случае изменяются во времени, и характеристика состояния будет определяться случайным процессом D(t). Таким образом, необходимо решать задачу о выбросах случайного процесса. При этом вероятность возникновения катастрофы
P(t) = P{D(t) > 0}.
Предположим, что D(t) – дифференцируемый случайный процесс,
.
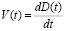Нас интересует вероятность того, что реализация случайного процесса D(t) пересечет нулевой уровень. Среднее число пересечений случайным процессом заданного уровня определялось рядом исследователей [4], [8].
В общем случае среднее число пересечений уровня 0 за время t (математическое ожидание числа выбросов):
,
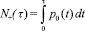для стационарного процесса:
N+(τ) = τ·p0.
В нашем случае для гауссовского стационарного процесса
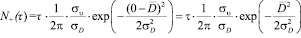, (4)
где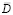 
– математическое ожидание случайного процесса;
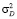– дисперсия случайного процесса;
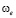– эффективная частота процесса 
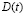, с-1.
Тогда
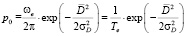.(5)
Временную плотность p0(t) можно трактовать как среднее число пересечений случайным процессом D(t) нулевого уровня в единицу времени. Для стационарного процесса плотность распределения ординат и скоростей не зависит от времени, следовательно, p0(t) = p0.
Во многих задачах практический интерес представляет вариант, при котором среднее число выбросов за данный промежуток времени достаточно мало и можно считать появления последовательных выбросов независимыми «редкими» событиями. В этом случае число появлений выбросов можно считать приближенно подчиняющимся закону распределения Пуассона [4], при этом единственным параметром, входящим в закон распределения, является математическое ожидание числа выбросов N+(τ).
Вероятность безотказной работы будет определяться как вероятность того, что за время t не произойдет ни одного отказа (выброса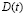 
за нулевой уровень):
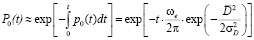. (6)
Вероятность отказа
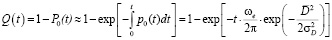. (7)
Средняя наработка до отказа (математическое ожидание наработки до выброса)
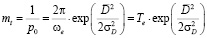. (8)
В работе А.В. Питухина [2] для оценки вероятности катастрофы сборки предложены аналитический метод и метод статистической линеаризации для случая, когда управляющие параметры a и b являются случайными величинами. Воспользуемся методом статистической линеаризации для оценки математического ожидания и дисперсии случайного процесса D(t) в случае, когда переменные управления являются стационарными случайными функциями (процессами). Очевидно
; 
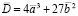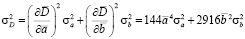, (9)
где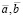 
– математические ожидания стационарных случайных процессов a(t) и b(t);
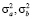– дисперсии стационарных случайных процессов a(t) и b(t).
Полученные зависимости (6–9) позволяют оценить вероятность безотказной работы различных элементов конструкций технологических машин. Весьма важна и задача оценки энергии деформирования элементов конструкций вплоть до их разрушения. Особенно это касается защитных каркасов кабин лесопромышленных тракторов.
Рассмотрим случай бокового нагружения кабины колесного скиддера ТЛК-4-01.
В данной конструкции основные деформации будут воспринимать защитный каркас и болт его крепления к несущей раме (рис. 1). Несложным пересчетом заменяем защитный каркас эквивалентной пружиной с жесткостью G и деформируемой силой F. Болт моделируем стержнем. Таким образом, получаем условную схему нагружения, энергетически эквивалентную исходной.
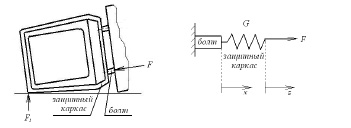
Рис. 1. Условная схема нагружения кабины трактора
Представим сопротивление стержня растяжению в виде зависимости:
F = Ax – Cx3, (10)
где F – нагрузка;
x – абсолютное удлинение стержня;
A, C – эмпирические коэффициенты.
Полная диаграмма растяжения стержня, описываемая зависимостью (10), представлена на рис. 2. Такие полные диаграммы деформирования (с падающей ветвью) могут быть получены на испытательных установках с большой жесткостью. В нашем случае жесткость защитного каркаса должна существенно превышать жесткость болта.
Полная потенциальная энергия системы определяется произведением соответствующих сил на перемещения:
,
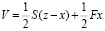где S – сила сопротивления деформации эквивалентной пружины;
z – условное перемещение активного конца эквивалентной пружины.
Выразив силы через перемещения, будем иметь:
.
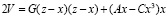После преобразований получим:
.
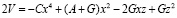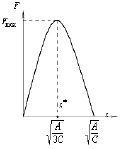
Рис. 2. Полная диаграмма растяжения стержня
Полученное выражение аналогично выражению (1), описывающему катастрофу сборки. Поверхность равновесия M определяется уравнением производной dVab(x)/dx (2), коэффициенты в котором определяются:
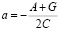; (11)
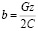. (12)
Допустим, что A, C, G, z – стационарные случайные функции с математическими ожиданиями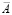 
, 
, 
, 
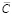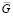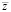и дисперсиями 
, 
, 
, 
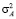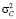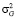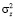. Согласно методу статистической линеаризации
; 
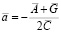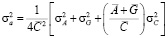; (13)
; 
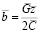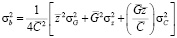. (14)
Используя формулы (6–9) с учетом (13), (14), можно определить вероятность катастрофы сборки (разрушения болта).
Численное решение задачи целесообразно осуществить в следующем порядке: определить жесткость G эквивалентной пружины, оценить коэффициенты A и C в полной диаграмме растяжения стержня (10), задать значения средних квадратических отклонений коэффициентов A, C и G.
Численное значение жесткости G эквивалентной пружины определялось методом конечных элементов с использованием пакета «Зенит». Получено значение G = 8700 Н/мм
Определим коэффициенты А и С в полной диаграмме растяжения стержня. Для этого пересчитаем Fmax и x* для стержня, моделирующего болт, через предел прочности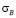 
и относительное удлинение 
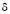соответствующей стали.
Для стали 30, согласно справочным материалам,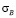 
= 500 МПа, δ = 20 %. При диаметре стержня d = 30 мм и длине l = 100 мм максимальная разрушающая стержень нагрузка и соответствующее ей абсолютное удлинение определяется:
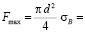353000 Н;
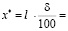20 мм.
Подставляя численные значения Fmax и x*, и решая систему уравнений
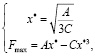
получим A = 26500 Н/мм, C = 22,1 Н/мм3.
Значения G, A и C полагаем случайными функциями с математическими ожиданиями, подсчитанными выше. Таким образом, численные значения задаем в следующем виде:
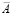= 26500 Н/мм, 
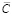= 22,1 Н/мм3, 
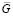= 8700 Н/мм;
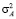= 2650 Н/мм, 
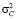= 2,21 Н/мм3, 
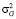= 870 Н/мм; 
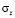= 0,1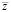 
.
Результаты расчетов представлены на рис. 3.
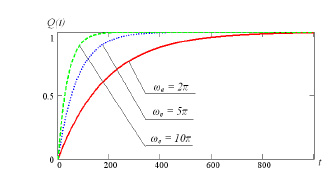
Рис. 3. Вероятность отказа при различных вариантах эффективных частот ωе случайного процесса D(t)
Работа выполнена при поддержке Программы стратегического развития (ПСР) Петрозаводского государственного университета в рамках реализации комплекса мероприятий по развитию научно-исследовательской деятельности на 2012–2016 гг.
Рецензенты:
Васильев С.Б., д.т.н., профессор, заведующий кафедрой Целлюлозно-бумажных и деревообрабатывающих производств Петрозаводского государственного университета, г. Петрозаводск;
Колесников Г.Н., д.т.н., профессор, заведующий кафедрой Механики, Петрозаводский государственный университет, г. Петрозаводск.
Работа поступила в редакцию 15.08.2014.